2020春北师大版七下数学5.2探索轴对称的性质同步练习(2课时含答案)
文档属性
| 名称 | 2020春北师大版七下数学5.2探索轴对称的性质同步练习(2课时含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 293.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-23 09:43:32 | ||
图片预览


文档简介
2020春北师大版七下数学5.2探索轴对称的性质同步练习
1.下列说法正确的是( )
A.如果点A,B关于直线MN对称,则AB垂直平分MN
B.如果△ABC≌△A′B′C′,则一定存在直线l,使△ABC和△A′B′C′关于l对称
C.若直线l同时垂直平分AA′,BB′,则线段AB=A′B′
D.如果△ABC中的点A在对称轴上,则点A没有对称点
2.[2016·南充]如图47?5,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是 ( )
图47?5
A.AM=BM B.AP=BN
C.∠MAP=∠MBP D.∠ANM=∠BNM
3.如图47?6,将矩形ABCD沿对角线折叠,使点C与点C′重合.若AB=2,则C′D的长为( )
图47?6
A.1 B.2
C.3 D.4
4.如图47?7,若∠AOB=45°,P是∠AOB内一点,分别作点P关于直线OA,OB的对称点P1,P2,连接OP1,OP2,则下列结论最正确的是( )
图47?7
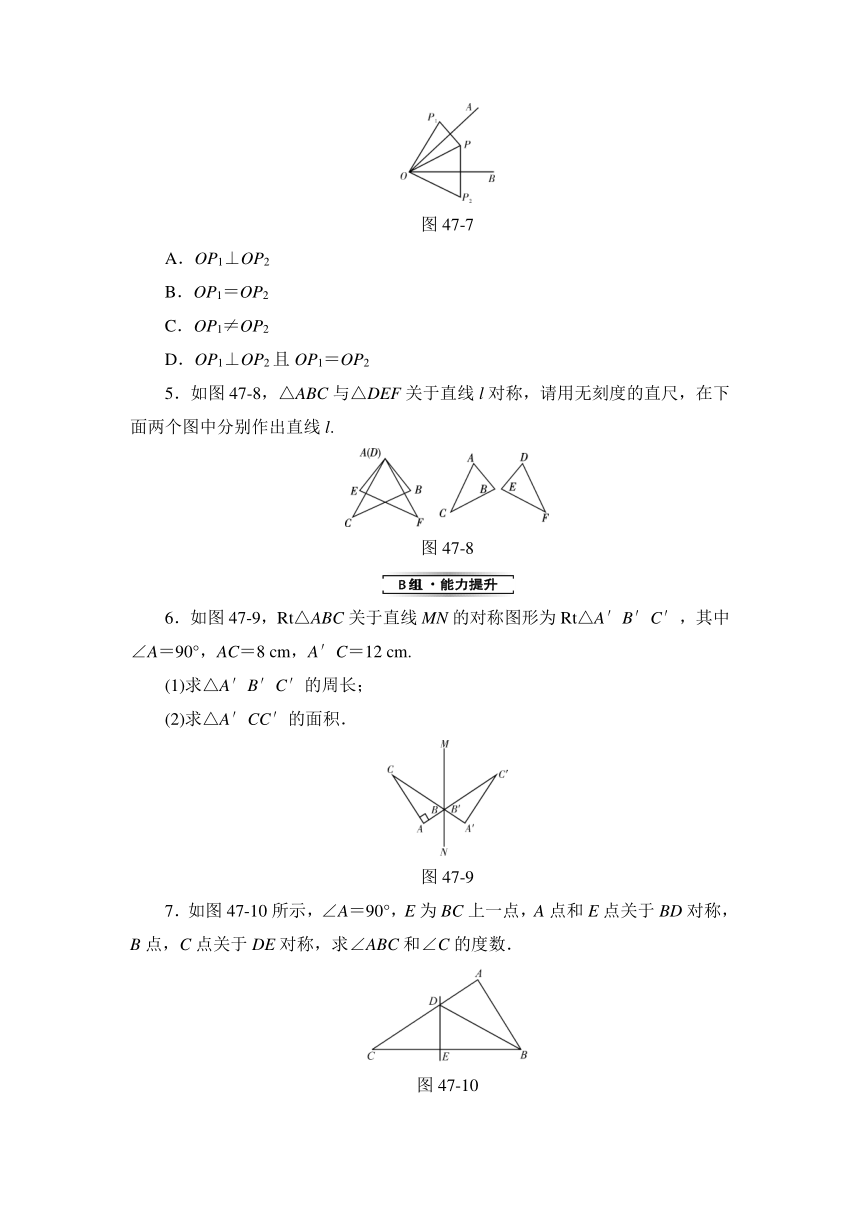
A.OP1⊥OP2
B.OP1=OP2
C.OP1≠OP2
D.OP1⊥OP2且OP1=OP2
5.如图47?8,△ABC与△DEF关于直线l对称,请用无刻度的直尺,在下面两个图中分别作出直线l.
图47?8
6.如图47?9,Rt△ABC关于直线MN的对称图形为Rt△A′B′C′,其中∠A=90°,AC=8 cm,A′C=12 cm.
(1)求△A′B′C′的周长;
(2)求△A′CC′的面积.
图47?9
7.如图47?10所示,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点,C点关于DE对称,求∠ABC和∠C的度数.
图47?10
8.如图47?11,∠AOB内有一点P,点P关于OA,OB的对称点为P1,P2,连接P1P2,交OA于M,交OB于N,若P1P2=5 cm,求△PMN的周长.
图47?11
参考答案
【分层作业】
1.C 2.B 3.B 4.D 5.略
6.(1)20 cm;(2)48 cm2.
7.∠ABC=60°,∠C=30°.
8.5 cm
2020春北师大版七下数学5.2探索轴对称的性质同步练习2
◆基础训练
一、选择题
1.以下结论正确的是( ).
A.两个全等的图形一定成轴对称
B.两个全等的图形一定是轴对称图形
C.两个成轴对称的图形一定全等
D.两个成轴对称的图形一定不全等
2.下列说法中正确的有( ).
①角的两边关于角平分线对称;
②两点关于连接它的线段的中垂线为对称;
③成轴对称的两个三角形的对应点,或对应线段,或对应角也分别成轴对称.
④到直线L距离相等的点关于L对称
A.1个 B.2个 C.3个 D.4个
3.下列说法错误的是( ).
A.等边三角形是轴对称图形;
B.轴对称图形的对应边相等,对应角相等;
C.成轴对称的两条线段必在对称轴一侧;
D.成轴对称的两个图形对应点的连线被对称轴垂直平分.
二、填空题
4.轴对称图形对应点连线被________,对应角对应线段都________.
5.设A、B两点关于直线MN成轴对称,则______垂直平分______.
三、解答题
6.找出图中是轴对称图形的图形,并找出两对对应点、两对对应线段、两对对应角.
7.如图,将正方形ABCD绕A点按逆时针方向旋转60°至正方形AB′C′D′,则旋转前后组成的图形是轴对称图形吗?若是轴对称图形,画出它的对称轴,并求出∠DAB′的度数.
◆能力提高
一、填空题
8.如图,矩形ABCD沿AE折叠,使点D落在BC边上的点F处,如果∠BAF=60°,那么∠DAE=_________.
9.已知Rt△ABC中,斜边AB=2BC,以直线AC为对称轴,点B的对称点是B′,如图所示,则与线段BC相等的线段是______,与线段AB相等的线段是_______和_______.与∠B相等的角是_______和_______,因此,∠B=________.
二、解答题
10.如图K-37-7,△ABC与△DEF关于直线MN对称,其中∠C=90°,AC=8 cm,DE=10 cm,BC=6 cm.
(1)连接AD,线段AD与MN的关系是什么?
(2)求∠F的度数;
(3)求△ABC的周长和△DEF的面积.
图K-37-7
参考答案
1.C 2.C 3.C 4.略 5.直线MN,线段AB
6.图A是轴对称图形.如图,若以EF为对称轴,由点A与点B,点M与点N,点C与点D等是对称点,线段AG与BH,CM与DN,PG与PH等是对应线段,∠A与∠B,∠C与∠D,∠AMC与∠BND等是对应角.
7.是轴对称图形,∠DAB′=30° 8.15°
9.B′C,BB′,AB′,∠BAB′,∠B′,60°
10.解:(1)因为△ABC与△DEF关于直线MN对称,所以MN垂直平分AD.
(2)因为△ABC与△DEF关于直线MN对称,所以△ABC≌△DEF,所以∠F=∠C=90°.
(3)因为AC=8 cm,DE=10 cm,BC=6 cm,所以AB=DE=10 cm,所以△ABC的周长=6+8+10=24(cm);
△DEF的面积=△ABC的面积=×6×8=24(cm2).
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
