人教高中数学选修2-3第一章1.2.3组合与组合数公式(2)课件(共16张PPT)
文档属性
| 名称 | 人教高中数学选修2-3第一章1.2.3组合与组合数公式(2)课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 247.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 22:10:32 | ||
图片预览






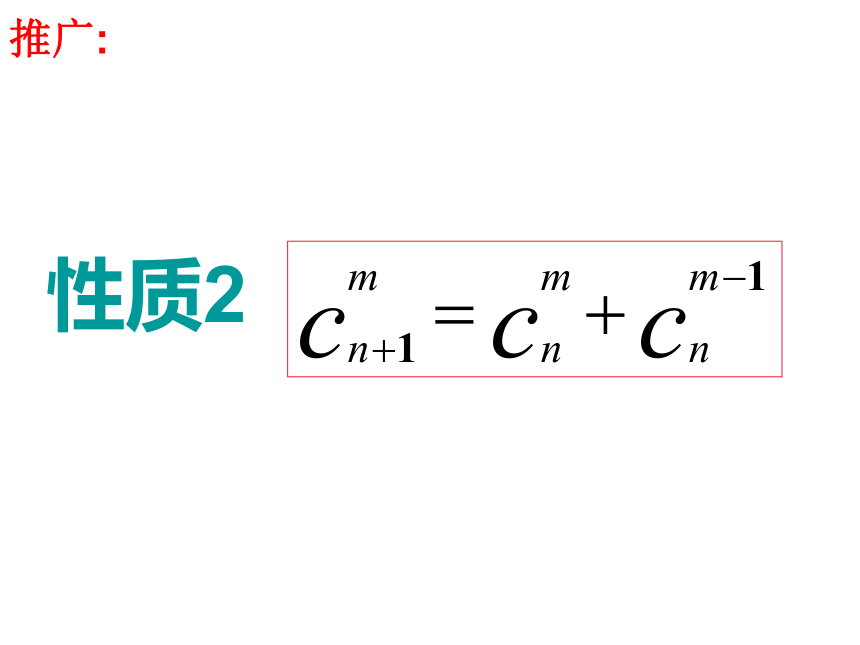
文档简介
(共16张PPT)
1.2.3组合数的性质和应用
一、组合的定义
二、组合数公式
复习
组合数的两个性质
3、性质1的应用
(1)当m> 时,利用这个公式,可使 的计算简化
如:
1、一个口袋内装有大小相同的7个白球和1个黑球.
⑴ 从口袋内取出3个球,共有多少种取法?
⑵ 从口袋内取出3个球,使其中含有1个黑球,有多少种取法?
⑶ 从口袋内取出3个球,使其中不含黑球,有多少种取法?
⑵
⑶
解:(1)
性质2
我们可以这样解释:从口袋内的8个球中所取出的3个球,可以分为两类:一类含有1个黑球,一类不含有黑球.因此根据分类计数原理,上述等式成立.
我们发现:
为什么呢
推广:
性质2
注:1? 公式特征:下标相同而上标差1的两个组合数之和,等于下标比原下标多1而上标与原组合数上标较大的相同的一个组合数.
2? 此性质的作用:恒等变形,简化运算.在今后学习“二项式定理”时,我们会看到它的主要应用.
例1 计算:
(4)解方程:
例2 求证:
证明:
⑴ 计算:
⑵ 求证:
=
+
+
⑶ 解方程:
(4) 计算:
推广:
练习:
例3、12件产品中有3件次品,9件正品,从中抽取5 件,
(1) 5件产品中没有次品的取法有多少种?
(2) 5件产品中有2件次品的取法有多种?
例4、从4台纯平彩电和5台超平彩电中选购3台,要求至少有纯平彩电和超平彩电各1台,问有多少种不同的选法?
例5、6本不同的书,按下列要求各有多少种不同的分法:
(1)分给甲、乙、丙三人,每人2本;
(2)分为三份,每份2本;
(3)分为三份,一份1本,一份2本,一份3本:
(4)分给甲、乙、丙三人,一人1本,一人2 本,一人 3本。
例6、某省的福利彩票中,不考虑次序的7个数码组成一注,7个数码中没有重复,每一个数码都选自数码1,2,…,36,如果电视直播公开摇奖时只有一个大奖,计算:
(1)公开摇奖时最多可以摇出多少不同的注;
(2)购买一注时的中奖率。
1.2.3组合数的性质和应用
一、组合的定义
二、组合数公式
复习
组合数的两个性质
3、性质1的应用
(1)当m> 时,利用这个公式,可使 的计算简化
如:
1、一个口袋内装有大小相同的7个白球和1个黑球.
⑴ 从口袋内取出3个球,共有多少种取法?
⑵ 从口袋内取出3个球,使其中含有1个黑球,有多少种取法?
⑶ 从口袋内取出3个球,使其中不含黑球,有多少种取法?
⑵
⑶
解:(1)
性质2
我们可以这样解释:从口袋内的8个球中所取出的3个球,可以分为两类:一类含有1个黑球,一类不含有黑球.因此根据分类计数原理,上述等式成立.
我们发现:
为什么呢
推广:
性质2
注:1? 公式特征:下标相同而上标差1的两个组合数之和,等于下标比原下标多1而上标与原组合数上标较大的相同的一个组合数.
2? 此性质的作用:恒等变形,简化运算.在今后学习“二项式定理”时,我们会看到它的主要应用.
例1 计算:
(4)解方程:
例2 求证:
证明:
⑴ 计算:
⑵ 求证:
=
+
+
⑶ 解方程:
(4) 计算:
推广:
练习:
例3、12件产品中有3件次品,9件正品,从中抽取5 件,
(1) 5件产品中没有次品的取法有多少种?
(2) 5件产品中有2件次品的取法有多种?
例4、从4台纯平彩电和5台超平彩电中选购3台,要求至少有纯平彩电和超平彩电各1台,问有多少种不同的选法?
例5、6本不同的书,按下列要求各有多少种不同的分法:
(1)分给甲、乙、丙三人,每人2本;
(2)分为三份,每份2本;
(3)分为三份,一份1本,一份2本,一份3本:
(4)分给甲、乙、丙三人,一人1本,一人2 本,一人 3本。
例6、某省的福利彩票中,不考虑次序的7个数码组成一注,7个数码中没有重复,每一个数码都选自数码1,2,…,36,如果电视直播公开摇奖时只有一个大奖,计算:
(1)公开摇奖时最多可以摇出多少不同的注;
(2)购买一注时的中奖率。
