北师大版2020年九年级数学下册3.7切线长定理课件(共41张PPT)
文档属性
| 名称 | 北师大版2020年九年级数学下册3.7切线长定理课件(共41张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 19:33:51 | ||
图片预览







文档简介
(共41张PPT)
*7 切线长定理
【知识再现】
切线的性质:圆的切线_______________________.?
垂直于过切点的半径
【新知预习】
阅读教材P94~P95,完成下面填空:
1.切线长定义
过圆外一点作圆的切线,这点和切点之间的_________
_______叫做这点到圆的切线长?
线段的
长度
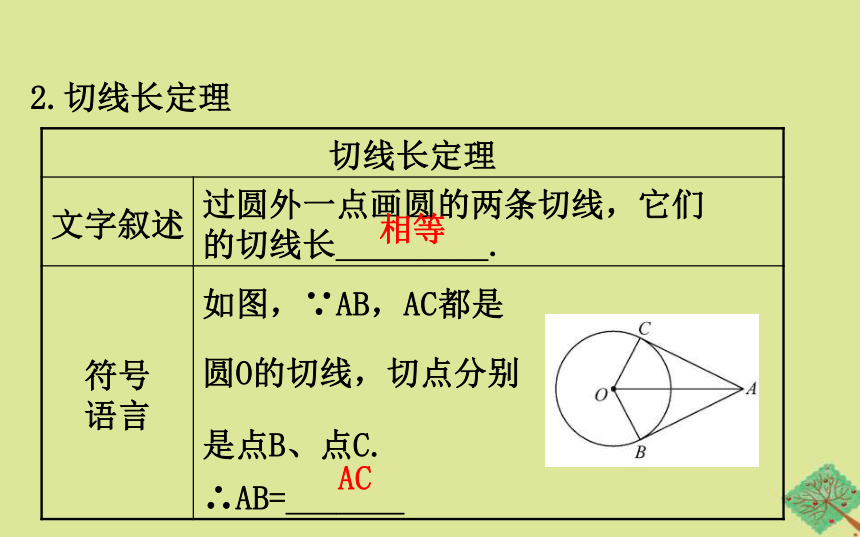
2.切线长定理
相等
AC
切线长定理
文字叙述 过圆外一点画圆的两条切线,它们
的切线长_________.?
符号
语言 如图,∵AB,AC都是
圆O的切线,切点分别
是点B、点C.
∴AB=_______?
【基础小练】
请自我检测一下预习的效果吧!
1.在圆外切四边形ABCD中,AB∶BC∶CD∶AD只可能是
( )
A.2∶3∶4∶5 B.3∶4∶6∶5
C.5∶4∶1∶3 D.3∶4∶2∶5
B
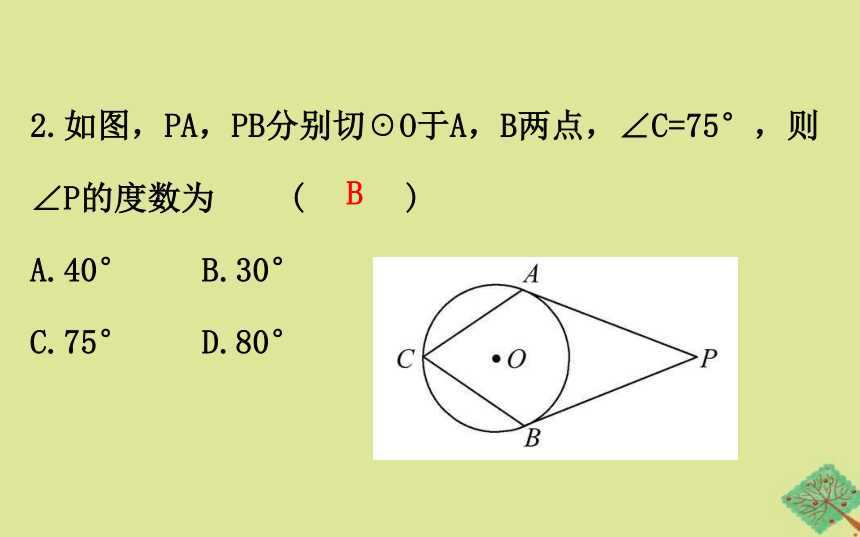
2.如图,PA,PB分别切☉O于A,B两点,∠C=75°,则
∠P的度数为 ( )
A.40° B.30°
C.75° D.80°
B
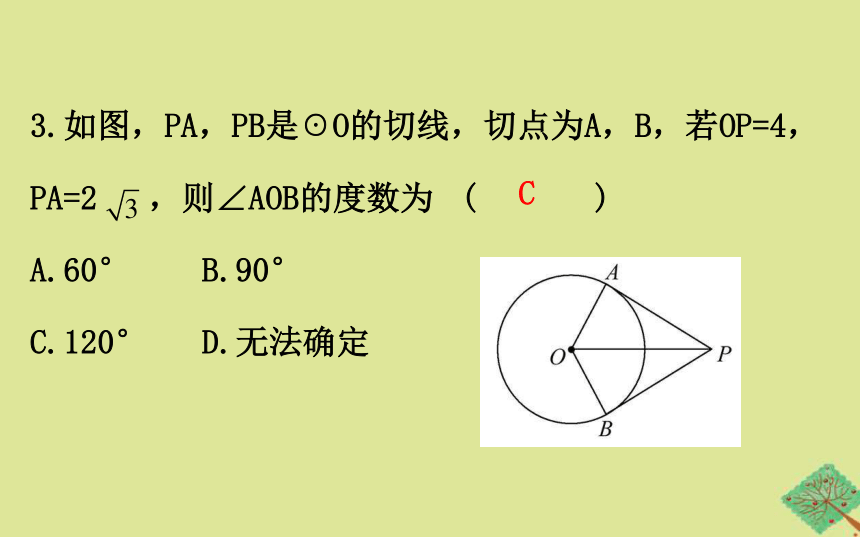
3.如图,PA,PB是☉O的切线,切点为A,B,若OP=4,
PA=2 ,则∠AOB的度数为 ( )
A.60° B.90°
C.120° D.无法确定
C
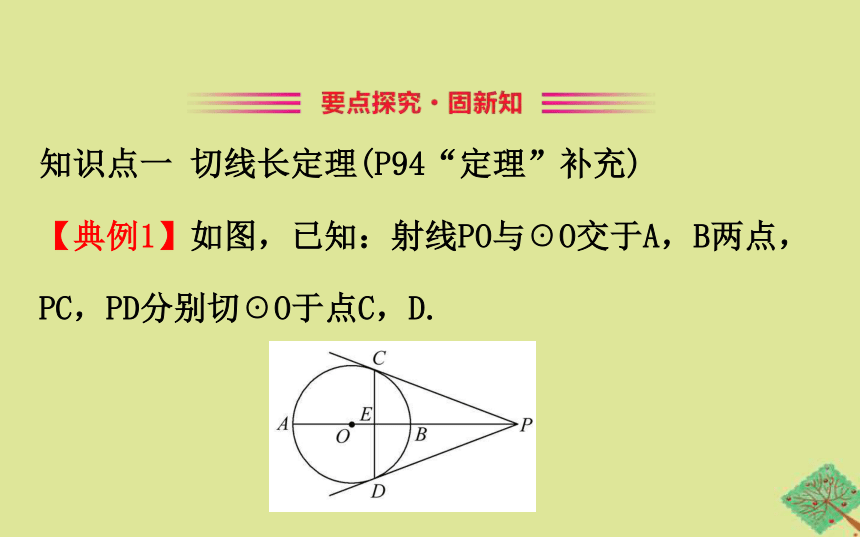
知识点一 切线长定理(P94“定理”补充)
【典例1】如图,已知:射线PO与☉O交于A,B两点,PC,PD分别切☉O于点C,D.
(1)请写出两个不同类型的正确结论.
(2)若CD=12,tan∠CPO= ,求PO的长.
【规范解答】(1)不同类型的正确结论有:
①PC=PD,②∠CPO=∠DPA,③CD⊥BA,④∠CEP=90°(答案不唯一).
(2)连接OC,∵PC,PD分别切☉O于点C,D,
∴PC=PD,∠CPO=∠DPA,∴CD⊥AB,
∵CD=12,∴DE=CE= CD=6.
∵tan∠CPO= ,∴在Rt△EPC中,PE=12,
∴由勾股定理得CP=6 ,
∵PC切☉O于点C,
∴∠OCP=90°,在Rt△OPC中,
∵tan∠CPO= ,∴ ,
∴OC=3 ,∴OP=15.
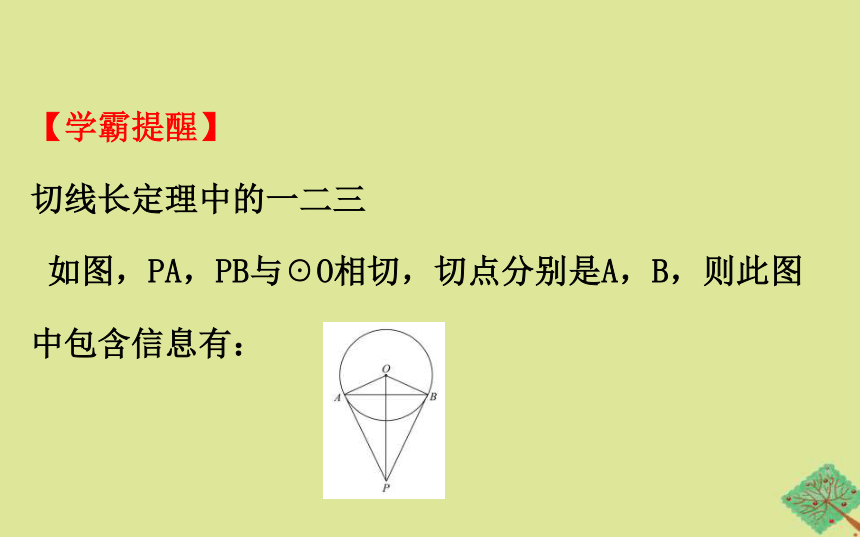
【学霸提醒】
切线长定理中的一二三
如图,PA,PB与☉O相切,切点分别是A,B,则此图中包含信息有:
1.一条角平分线:即PO平分∠APB且平分∠AOB.
2.两个等腰三角形:△PAB,△AOB是等腰三角形.
3.三个垂直:即OA⊥PA,OB⊥PB,PO⊥AB.
【题组训练】
1.(2019·深圳模拟)如图,AB是☉O的直径,点C为
☉O外一点,CA,CD是☉O的切线,A,D为切点,连接
BD,AD.若∠ACD=48°,则∠DBA的大小是 ( )
A.32° B.48°
C.60° D.66°
D
★2.(2019·宜兴二模)如图,PA,PB切☉O于点A,B,
PA=10,CD切☉O于点E,交PA,PB于C,D两点,则
△PCD的周长是 ( )
A.10 B.18
C.20 D.22
C
★3.如图,PA,PB是☉O的两条切线,A,B是切点,若
∠APB=60°,PO=2,则☉O的半径等于______.?
.
1
★★4.如图,PA,PB是☉O的切线,CD切☉O于点E,△PCD的周长为12,∠APB=60°.求:
.
(1)PA的长.
(2)∠COD的度数.
解:(1)∵CA,CE都是圆O的切线,∴CA=CE,同理DE=DB,PA=PB,∴三角形PCD的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,即PA的长为6.
(2)∵∠P=60°,∴∠PCE+∠PDE=120°,
∴∠ACD+∠CDB=360°-120°=240°,
∵CA,CE是圆O的切线,∴∠OCE=∠OCA=
∠ACD;同理:∠ODE= ∠CDB,
∴∠OCE+∠ODE= (∠ACD+∠CDB)=120°,
∴∠COD=180-120°=60°.
知识点二 切线长定理的应用(P95“想一想”拓展)
【典例2】如图,☉O内切于四边形ABCD,AB=10,
BC=7,CD=8,则AD的长度为 ( )
A.8 B.9
C.10 D.11
D
【思路点拨】根据圆外切四边形的性质对边和相等进而得出AD的长.
【学霸提醒】
切线长定理五类应用
1.求角度.
2.求线段的长度.
3.证线段相等.
4.证线段对应成比例.
5.证线段平行.
【题组训练】
1.(2019·常州金坛区期中)如图,AB,AC,BD是☉O的
切线,切点分别是P,C,D.若AB=5,AC=3,则BD的长
是 ( )
A.4 B.3
C.2 D.1
C
★2.如图,△ABC是一张周长为17 cm的三角形的纸片,
BC=5 cm,☉O是它的内切圆,李明准备用剪刀在☉O的
右侧沿着与☉O相切的任意一条直线MN剪下△AMN,则
剪下的三角形的周长为 ( )
.
B
A.12 cm
B.7 cm
C.6 cm
D.随直线MN的变化而变化
★3.如图,☉O是四边形ABCD的内切圆,下列结论一定
正确的有_______个:?
①AF=BG;②CG=CH;③AB+CD=AD+BC;
④BGA.1 B.2
C.3 D.4
B
★★4.如图,Rt△ABC中,∠ACB=90°,以AC为直径的
☉O与AB边交于点D,过点D作☉O的切线,交BC于点E.
.
(1)求证:BE=CE.
(2)若以O,D,E,C为顶点的四边形是
正方形,☉O的半径为r,求△ABC的面积.
解:(1)连接CD,由AC是直径知CD⊥AB.
∵DE,CE都是切线,
∴DE=CE,
∠EDC=∠ECD.
又∠B+∠ECD=90°,
∠BDE+∠EDC=90°;
∴∠B=∠BDE,∴BE=DE,从而BE=CE.
(2)连接OD,当以O,D,E,C为顶点的四边形是正方形时,DE=EC=OC=OD=r.
∴BE=r,即△ABC是一个等腰直角三角形,
∴AC=BC=2r,S△ABC=2r2.
【火眼金睛】
已知:PA,PB是☉O的切线,A,B是切点,点C是 上
的一个动点,若∠P=40°,求∠ACB的度数.
正解:另一种情况,若点C在劣弧AB上,如图C2
的位置,由圆内接四边形的性质可得∠AC2B+∠AC1B=180°,
∴∠AC2B=180°-70°=110°,
综上所述∠ACB=70°或110°.
【一题多变】
如图,AB,BC,CD分别与☉O相切于E,F,G,且AB∥CD,BO=6,CO=8.判断△OBC的形状,并证明你的结论.
解:△OBC是直角三角形.
证明:∵AB,BC,CD分别与☉O相切于E,F,G,
∴∠OBE=∠OBF= ∠EBF,∠OCG=∠OCF= ∠GCF,
∵AB∥CD,∴∠EBF+∠GCF=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°,∴△OBC是直角三角形.
【母题变式】
【变式一】(变换条件和问法)如图,在梯形ABCD中,AB∥CD,☉O为内切圆,E为切点.
求证:AO2=AE·AD.
证明:根据切线长定理可知:
∠OAE+∠ODA= (∠BAD+∠ADC)=90°,
∴∠AOD=90°,
∵∠OAE=∠OAE,∠AOD=∠AEO=90°,
∴△AOE∽△ADO,
∴ ,即AO2=AE·AD.
【变式二】(变换问法)如图,AB,BC,CD分别与☉O相切于E,F,G,且AB∥CD,BO=6,CO=8.求☉O的半径OF的长.
解:∵AB,BC,CD分别与☉O相切于E,F,G,
∴∠OBE=∠OBF= ∠EBF,∠OCG=∠OCF= ∠GCF,
∵AB∥CD,∴∠EBF+∠GCF=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°,∴△OBC是直角三角形;
∵AB,BC,CD分别与☉O相切于E,F,G,
∴OF⊥BC,∴OF= =4.8.
*7 切线长定理
【知识再现】
切线的性质:圆的切线_______________________.?
垂直于过切点的半径
【新知预习】
阅读教材P94~P95,完成下面填空:
1.切线长定义
过圆外一点作圆的切线,这点和切点之间的_________
_______叫做这点到圆的切线长?
线段的
长度
2.切线长定理
相等
AC
切线长定理
文字叙述 过圆外一点画圆的两条切线,它们
的切线长_________.?
符号
语言 如图,∵AB,AC都是
圆O的切线,切点分别
是点B、点C.
∴AB=_______?
【基础小练】
请自我检测一下预习的效果吧!
1.在圆外切四边形ABCD中,AB∶BC∶CD∶AD只可能是
( )
A.2∶3∶4∶5 B.3∶4∶6∶5
C.5∶4∶1∶3 D.3∶4∶2∶5
B
2.如图,PA,PB分别切☉O于A,B两点,∠C=75°,则
∠P的度数为 ( )
A.40° B.30°
C.75° D.80°
B
3.如图,PA,PB是☉O的切线,切点为A,B,若OP=4,
PA=2 ,则∠AOB的度数为 ( )
A.60° B.90°
C.120° D.无法确定
C
知识点一 切线长定理(P94“定理”补充)
【典例1】如图,已知:射线PO与☉O交于A,B两点,PC,PD分别切☉O于点C,D.
(1)请写出两个不同类型的正确结论.
(2)若CD=12,tan∠CPO= ,求PO的长.
【规范解答】(1)不同类型的正确结论有:
①PC=PD,②∠CPO=∠DPA,③CD⊥BA,④∠CEP=90°(答案不唯一).
(2)连接OC,∵PC,PD分别切☉O于点C,D,
∴PC=PD,∠CPO=∠DPA,∴CD⊥AB,
∵CD=12,∴DE=CE= CD=6.
∵tan∠CPO= ,∴在Rt△EPC中,PE=12,
∴由勾股定理得CP=6 ,
∵PC切☉O于点C,
∴∠OCP=90°,在Rt△OPC中,
∵tan∠CPO= ,∴ ,
∴OC=3 ,∴OP=15.
【学霸提醒】
切线长定理中的一二三
如图,PA,PB与☉O相切,切点分别是A,B,则此图中包含信息有:
1.一条角平分线:即PO平分∠APB且平分∠AOB.
2.两个等腰三角形:△PAB,△AOB是等腰三角形.
3.三个垂直:即OA⊥PA,OB⊥PB,PO⊥AB.
【题组训练】
1.(2019·深圳模拟)如图,AB是☉O的直径,点C为
☉O外一点,CA,CD是☉O的切线,A,D为切点,连接
BD,AD.若∠ACD=48°,则∠DBA的大小是 ( )
A.32° B.48°
C.60° D.66°
D
★2.(2019·宜兴二模)如图,PA,PB切☉O于点A,B,
PA=10,CD切☉O于点E,交PA,PB于C,D两点,则
△PCD的周长是 ( )
A.10 B.18
C.20 D.22
C
★3.如图,PA,PB是☉O的两条切线,A,B是切点,若
∠APB=60°,PO=2,则☉O的半径等于______.?
.
1
★★4.如图,PA,PB是☉O的切线,CD切☉O于点E,△PCD的周长为12,∠APB=60°.求:
.
(1)PA的长.
(2)∠COD的度数.
解:(1)∵CA,CE都是圆O的切线,∴CA=CE,同理DE=DB,PA=PB,∴三角形PCD的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,即PA的长为6.
(2)∵∠P=60°,∴∠PCE+∠PDE=120°,
∴∠ACD+∠CDB=360°-120°=240°,
∵CA,CE是圆O的切线,∴∠OCE=∠OCA=
∠ACD;同理:∠ODE= ∠CDB,
∴∠OCE+∠ODE= (∠ACD+∠CDB)=120°,
∴∠COD=180-120°=60°.
知识点二 切线长定理的应用(P95“想一想”拓展)
【典例2】如图,☉O内切于四边形ABCD,AB=10,
BC=7,CD=8,则AD的长度为 ( )
A.8 B.9
C.10 D.11
D
【思路点拨】根据圆外切四边形的性质对边和相等进而得出AD的长.
【学霸提醒】
切线长定理五类应用
1.求角度.
2.求线段的长度.
3.证线段相等.
4.证线段对应成比例.
5.证线段平行.
【题组训练】
1.(2019·常州金坛区期中)如图,AB,AC,BD是☉O的
切线,切点分别是P,C,D.若AB=5,AC=3,则BD的长
是 ( )
A.4 B.3
C.2 D.1
C
★2.如图,△ABC是一张周长为17 cm的三角形的纸片,
BC=5 cm,☉O是它的内切圆,李明准备用剪刀在☉O的
右侧沿着与☉O相切的任意一条直线MN剪下△AMN,则
剪下的三角形的周长为 ( )
.
B
A.12 cm
B.7 cm
C.6 cm
D.随直线MN的变化而变化
★3.如图,☉O是四边形ABCD的内切圆,下列结论一定
正确的有_______个:?
①AF=BG;②CG=CH;③AB+CD=AD+BC;
④BG
C.3 D.4
B
★★4.如图,Rt△ABC中,∠ACB=90°,以AC为直径的
☉O与AB边交于点D,过点D作☉O的切线,交BC于点E.
.
(1)求证:BE=CE.
(2)若以O,D,E,C为顶点的四边形是
正方形,☉O的半径为r,求△ABC的面积.
解:(1)连接CD,由AC是直径知CD⊥AB.
∵DE,CE都是切线,
∴DE=CE,
∠EDC=∠ECD.
又∠B+∠ECD=90°,
∠BDE+∠EDC=90°;
∴∠B=∠BDE,∴BE=DE,从而BE=CE.
(2)连接OD,当以O,D,E,C为顶点的四边形是正方形时,DE=EC=OC=OD=r.
∴BE=r,即△ABC是一个等腰直角三角形,
∴AC=BC=2r,S△ABC=2r2.
【火眼金睛】
已知:PA,PB是☉O的切线,A,B是切点,点C是 上
的一个动点,若∠P=40°,求∠ACB的度数.
正解:另一种情况,若点C在劣弧AB上,如图C2
的位置,由圆内接四边形的性质可得∠AC2B+∠AC1B=180°,
∴∠AC2B=180°-70°=110°,
综上所述∠ACB=70°或110°.
【一题多变】
如图,AB,BC,CD分别与☉O相切于E,F,G,且AB∥CD,BO=6,CO=8.判断△OBC的形状,并证明你的结论.
解:△OBC是直角三角形.
证明:∵AB,BC,CD分别与☉O相切于E,F,G,
∴∠OBE=∠OBF= ∠EBF,∠OCG=∠OCF= ∠GCF,
∵AB∥CD,∴∠EBF+∠GCF=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°,∴△OBC是直角三角形.
【母题变式】
【变式一】(变换条件和问法)如图,在梯形ABCD中,AB∥CD,☉O为内切圆,E为切点.
求证:AO2=AE·AD.
证明:根据切线长定理可知:
∠OAE+∠ODA= (∠BAD+∠ADC)=90°,
∴∠AOD=90°,
∵∠OAE=∠OAE,∠AOD=∠AEO=90°,
∴△AOE∽△ADO,
∴ ,即AO2=AE·AD.
【变式二】(变换问法)如图,AB,BC,CD分别与☉O相切于E,F,G,且AB∥CD,BO=6,CO=8.求☉O的半径OF的长.
解:∵AB,BC,CD分别与☉O相切于E,F,G,
∴∠OBE=∠OBF= ∠EBF,∠OCG=∠OCF= ∠GCF,
∵AB∥CD,∴∠EBF+∠GCF=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°,∴△OBC是直角三角形;
∵AB,BC,CD分别与☉O相切于E,F,G,
∴OF⊥BC,∴OF= =4.8.
