北师大版2020年九年级数学下册3.1圆课件(共45张PPT)
文档属性
| 名称 | 北师大版2020年九年级数学下册3.1圆课件(共45张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 20:03:37 | ||
图片预览










文档简介
(共45张PPT)
第三章 圆
1 圆
【知识再现】
圆:在平面内,一条线段OA绕着它固定的一个端点
O_____________,另一个端点A所形成的图形,定点
O叫做_________,线段OA叫做_________.?
旋转一周
圆心
半径
【新知预习】
阅读教材P65~66,解决以下问题:
1.圆的定义
(1)集合性定义:平面上到定点的_________等于定
长的___________组成的图形叫做圆,其中,定点称
为_________,定长称为_________.?
距离
所有点
圆心
半径
(2)记法:以点O为圆心的圆记作________,
读作“________”.?
☉O
圆O
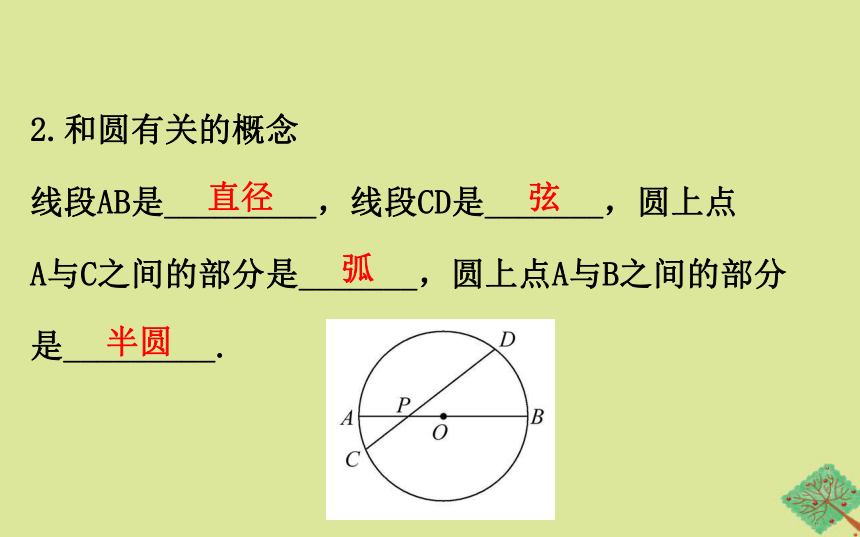
2.和圆有关的概念
线段AB是_________,线段CD是_______,圆上点
A与C之间的部分是_______,圆上点A与B之间的部分
是_________.?
直径
弦
弧
半圆
归纳:
(1)弦和直径:弦是连接圆上任意两点间的_________,
直径是经过_________的弦.?
(2)弧:_________任意两点间的部分叫做圆弧,简称
_______.?
线段
圆心
圆上
弧
(3)等圆和等弧:_________相等的圆叫等圆,在
_______________中,能够互相_________的弧叫
做等弧.?
半径
同圆或等圆
重合
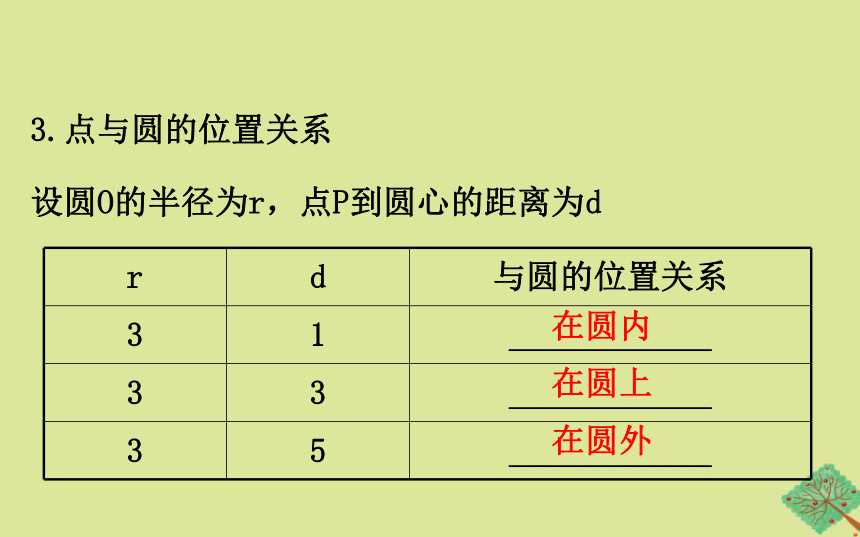
3.点与圆的位置关系
设圆O的半径为r,点P到圆心的距离为d
在圆内 ?
在圆上 ?
在圆外 ?
r d 与圆的位置关系
3 1 ____________
3 3 ____________
3 5 ____________
归纳:
设圆O的半径是r,点P到圆心的距离OP=d,则有
(1)点P在圆内?d______r.?
(2)点P在圆上?d______r.?
(3)点P在圆外?d______r.?
<
=
>
【基础小练】
请自我检测一下预习的效果吧!
1.下列说法:①半圆是弧;
②弧是半圆;③圆中的弧分为优弧和劣弧.
其中正确的个数有 ( )
A.0 B.1 C.2 D.3
B
2.以2 cm为半径可以画_________个圆;以点O为圆心
可以画_________个圆;以点O为圆心,以2 cm为半径
可以画_______个圆.?
3.已知☉O的半径r=2 cm,当OP=_________时,点P在
☉O上;当OA=1 cm时,点A在圆_______;当OB=4 cm
时,点B在圆_______.?
无数
无数
一
2 cm
内
外
知识点一 圆的认识
(P65“圆的定义”拓展)
【典例1】已知点P,Q,且PQ=4 cm,
(1)画出下列图形:到点P的距离等于2 cm的点的集合;到点Q的距离等于3 cm的点的集合.
(2)在所画图中,到点P的距离等于2 cm,且到点Q的距离等于3 cm的点有几个?请在图中将它们表示出来.
【尝试解答】(1)到点P的距离等于2 cm的点的集合
如图中☉______;到点Q的距离等于3 cm的点的集合
如图中☉______.?
P
Q
(2)到点P的距离等于2 cm,且到点Q的距离等于3 cm
的点有______个,如图中_________.?
2
C,D
【题组训练】
1.以已知点O为圆心作圆,可以作 ( )
A.1个 B.2个 C.3个 D.无数个
D
★2.下列说法正确的是 ( )
A.直径是弦,弦是直径
B.过圆心的直线是直径
C.圆中最长的弦是直径
D.直径只有二条
C
★3.(2019·鄞州期末)已知AB是半径为5的圆的
一条弦,则AB的长不可能是 ( )
A.4 B.8 C.10 D.12
D
★★4.(2019·菏泽单县期末)如图,在☉O中,
弦的条数是 ( )
A.2 B.3
C.4 D.以上均不正确
C
★★5.(2019·常熟月考)如图,CD是☉O的直径,
∠EOD=84°,AE交☉O于点B,且AB=OC,则∠A的
度数是_________. ?
28°
【我要做学霸】
圆中的易混淆概念
(1)弦与直径的区别:直径是_________的弦,但弦
不一定是_________,半径不是弦.?
(2)弧与半圆的区别:半圆是弧,是整圆的一半,
但不是_________的弧,同时弧不一定是半圆.?
最长
直径
最长
知识点二 点与圆的位置关系
(P66“做一做”拓展)
【典例2】如图,在Rt△ABC中,∠C=90°,AC=4,点O是BC上一点,且OC=3,点E是AO的中点,如以点O为圆心,OC为半径作圆,求点E和☉O的位置关系.
【尝试解答】在Rt△ACO中,∠C=90°,AC=4,OC=3,
∴OA=___________=5.……………………勾股定理?
又∵点E是AO的中点,
∴OE=_______=_______. ………………中点的定义?
∵OE= <3 =OC,?
∴点E在☉O 内 . …………………………得出结论?
【学霸提醒】判断点与圆的位置关系的步骤
1.求点到圆心的距离d.
2.比较d与r的大小.
①d>r?点在圆外;
②d=r?点在圆上;
③d【题组训练】
1.(2019·潜山县期末)已知☉O的半径为2,一点
P到圆心O的距离为4,则点P在 ( )
A.圆内 B.圆上
C.圆外 D.无法确定
C
★2.(2019·瑞安市期末)已知点P在半径为5 cm的
圆内,则点P到圆心的距离可以是 ( )
A.4 cm B.5 cm C.6 cm D.7 cm
A
★3.(2019·温州期末)如图,在△ABC中,∠C=90°,
AB=5,AC=4,D,E分别是AC,AB的中点,若作半径为
2的☉D,则下列选项中的点在☉D外的是 ( )
A.点A B.点B
C.点C D.点E
B
★4.已知☉A的直径是8,点A的坐标是(3,4),那么
坐标原点O在☉A_______.(填“内”“上”或“外”)?
外
★★5.(分类讨论题)如图,线段AB=8 cm,点D从A点出
发沿AB向B点匀速运动,速度为1 cm/s,同时点C 从
B点出发沿BA向A点以相同速度运动,以点C为圆心,
2 cm长为半径作☉C,点D到达B点时☉C也停止运动,
设运动时间为t s,则点D在☉C内部时t的取值范围是
__________. ?
3【火眼金睛】
在同一平面内一个点到圆上的最大距离是7 cm,最小距离是1 cm,求这个圆的半径.
正解:如图,设已知点为P,
若直径AB=PB-PA=7-1=6(cm),
则圆的半径为3 cm;
若直径AB=PB+PA=7+1=8(cm),
则圆的半径为4 cm.
【一题多变】
如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作☉C,半径为r.
(1)当r取什么值时,点A,B在☉C外.
(2)当r在什么范围时,点A在☉C内,点B在☉C外.
解:(1)当0(2)当3【母题变式】
【变式一】(变换条件)已知☉O和直线L,过圆心O作
OP⊥L,P为垂足,A,B,C为直线L上三个点,且PA=
2 cm,PB=3 cm,PC=4 cm,若☉O的半径为5 cm,OP=
4 cm,判断A,B,C三点与☉O的位置关系.
解:如图,当PA=2 cm,OA= <5,
点A在☉O内部;
当PB=3 cm,OB=5=r,点B在☉O上;
当PC=4 cm,OC= >5=r,点C在☉O外.
【变式二】(变换问法)如图所示,已知矩形ABCD的边AB=3 cm,AD=4 cm.
(1)以点A为圆心,4 cm为半径作☉A,则点B,C,D与☉A的位置关系如何?
(2)若以点A为圆心作☉A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,则☉A的半径r的取值范围是什么?
解:(1)连接AC,
∵AB=3 cm,AD=4 cm,
∴AC=5 cm,
∴点B在☉A内,点D在☉A上,点C在☉A外.
(2)∵以点A为圆心作☉A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,
∴☉A的半径r的取值范围是3 cm
第三章 圆
1 圆
【知识再现】
圆:在平面内,一条线段OA绕着它固定的一个端点
O_____________,另一个端点A所形成的图形,定点
O叫做_________,线段OA叫做_________.?
旋转一周
圆心
半径
【新知预习】
阅读教材P65~66,解决以下问题:
1.圆的定义
(1)集合性定义:平面上到定点的_________等于定
长的___________组成的图形叫做圆,其中,定点称
为_________,定长称为_________.?
距离
所有点
圆心
半径
(2)记法:以点O为圆心的圆记作________,
读作“________”.?
☉O
圆O
2.和圆有关的概念
线段AB是_________,线段CD是_______,圆上点
A与C之间的部分是_______,圆上点A与B之间的部分
是_________.?
直径
弦
弧
半圆
归纳:
(1)弦和直径:弦是连接圆上任意两点间的_________,
直径是经过_________的弦.?
(2)弧:_________任意两点间的部分叫做圆弧,简称
_______.?
线段
圆心
圆上
弧
(3)等圆和等弧:_________相等的圆叫等圆,在
_______________中,能够互相_________的弧叫
做等弧.?
半径
同圆或等圆
重合
3.点与圆的位置关系
设圆O的半径为r,点P到圆心的距离为d
在圆内 ?
在圆上 ?
在圆外 ?
r d 与圆的位置关系
3 1 ____________
3 3 ____________
3 5 ____________
归纳:
设圆O的半径是r,点P到圆心的距离OP=d,则有
(1)点P在圆内?d______r.?
(2)点P在圆上?d______r.?
(3)点P在圆外?d______r.?
<
=
>
【基础小练】
请自我检测一下预习的效果吧!
1.下列说法:①半圆是弧;
②弧是半圆;③圆中的弧分为优弧和劣弧.
其中正确的个数有 ( )
A.0 B.1 C.2 D.3
B
2.以2 cm为半径可以画_________个圆;以点O为圆心
可以画_________个圆;以点O为圆心,以2 cm为半径
可以画_______个圆.?
3.已知☉O的半径r=2 cm,当OP=_________时,点P在
☉O上;当OA=1 cm时,点A在圆_______;当OB=4 cm
时,点B在圆_______.?
无数
无数
一
2 cm
内
外
知识点一 圆的认识
(P65“圆的定义”拓展)
【典例1】已知点P,Q,且PQ=4 cm,
(1)画出下列图形:到点P的距离等于2 cm的点的集合;到点Q的距离等于3 cm的点的集合.
(2)在所画图中,到点P的距离等于2 cm,且到点Q的距离等于3 cm的点有几个?请在图中将它们表示出来.
【尝试解答】(1)到点P的距离等于2 cm的点的集合
如图中☉______;到点Q的距离等于3 cm的点的集合
如图中☉______.?
P
Q
(2)到点P的距离等于2 cm,且到点Q的距离等于3 cm
的点有______个,如图中_________.?
2
C,D
【题组训练】
1.以已知点O为圆心作圆,可以作 ( )
A.1个 B.2个 C.3个 D.无数个
D
★2.下列说法正确的是 ( )
A.直径是弦,弦是直径
B.过圆心的直线是直径
C.圆中最长的弦是直径
D.直径只有二条
C
★3.(2019·鄞州期末)已知AB是半径为5的圆的
一条弦,则AB的长不可能是 ( )
A.4 B.8 C.10 D.12
D
★★4.(2019·菏泽单县期末)如图,在☉O中,
弦的条数是 ( )
A.2 B.3
C.4 D.以上均不正确
C
★★5.(2019·常熟月考)如图,CD是☉O的直径,
∠EOD=84°,AE交☉O于点B,且AB=OC,则∠A的
度数是_________. ?
28°
【我要做学霸】
圆中的易混淆概念
(1)弦与直径的区别:直径是_________的弦,但弦
不一定是_________,半径不是弦.?
(2)弧与半圆的区别:半圆是弧,是整圆的一半,
但不是_________的弧,同时弧不一定是半圆.?
最长
直径
最长
知识点二 点与圆的位置关系
(P66“做一做”拓展)
【典例2】如图,在Rt△ABC中,∠C=90°,AC=4,点O是BC上一点,且OC=3,点E是AO的中点,如以点O为圆心,OC为半径作圆,求点E和☉O的位置关系.
【尝试解答】在Rt△ACO中,∠C=90°,AC=4,OC=3,
∴OA=___________=5.……………………勾股定理?
又∵点E是AO的中点,
∴OE=_______=_______. ………………中点的定义?
∵OE= <3 =OC,?
∴点E在☉O 内 . …………………………得出结论?
【学霸提醒】判断点与圆的位置关系的步骤
1.求点到圆心的距离d.
2.比较d与r的大小.
①d>r?点在圆外;
②d=r?点在圆上;
③d
1.(2019·潜山县期末)已知☉O的半径为2,一点
P到圆心O的距离为4,则点P在 ( )
A.圆内 B.圆上
C.圆外 D.无法确定
C
★2.(2019·瑞安市期末)已知点P在半径为5 cm的
圆内,则点P到圆心的距离可以是 ( )
A.4 cm B.5 cm C.6 cm D.7 cm
A
★3.(2019·温州期末)如图,在△ABC中,∠C=90°,
AB=5,AC=4,D,E分别是AC,AB的中点,若作半径为
2的☉D,则下列选项中的点在☉D外的是 ( )
A.点A B.点B
C.点C D.点E
B
★4.已知☉A的直径是8,点A的坐标是(3,4),那么
坐标原点O在☉A_______.(填“内”“上”或“外”)?
外
★★5.(分类讨论题)如图,线段AB=8 cm,点D从A点出
发沿AB向B点匀速运动,速度为1 cm/s,同时点C 从
B点出发沿BA向A点以相同速度运动,以点C为圆心,
2 cm长为半径作☉C,点D到达B点时☉C也停止运动,
设运动时间为t s,则点D在☉C内部时t的取值范围是
__________. ?
3
在同一平面内一个点到圆上的最大距离是7 cm,最小距离是1 cm,求这个圆的半径.
正解:如图,设已知点为P,
若直径AB=PB-PA=7-1=6(cm),
则圆的半径为3 cm;
若直径AB=PB+PA=7+1=8(cm),
则圆的半径为4 cm.
【一题多变】
如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作☉C,半径为r.
(1)当r取什么值时,点A,B在☉C外.
(2)当r在什么范围时,点A在☉C内,点B在☉C外.
解:(1)当0
【变式一】(变换条件)已知☉O和直线L,过圆心O作
OP⊥L,P为垂足,A,B,C为直线L上三个点,且PA=
2 cm,PB=3 cm,PC=4 cm,若☉O的半径为5 cm,OP=
4 cm,判断A,B,C三点与☉O的位置关系.
解:如图,当PA=2 cm,OA= <5,
点A在☉O内部;
当PB=3 cm,OB=5=r,点B在☉O上;
当PC=4 cm,OC= >5=r,点C在☉O外.
【变式二】(变换问法)如图所示,已知矩形ABCD的边AB=3 cm,AD=4 cm.
(1)以点A为圆心,4 cm为半径作☉A,则点B,C,D与☉A的位置关系如何?
(2)若以点A为圆心作☉A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,则☉A的半径r的取值范围是什么?
解:(1)连接AC,
∵AB=3 cm,AD=4 cm,
∴AC=5 cm,
∴点B在☉A内,点D在☉A上,点C在☉A外.
(2)∵以点A为圆心作☉A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,
∴☉A的半径r的取值范围是3 cm
