沪科版九下:24.2.4圆的确定 教案(表格式)
文档属性
| 名称 | 沪科版九下:24.2.4圆的确定 教案(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 57.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 21:30:38 | ||
图片预览


文档简介
课题名称
24.2.4圆的确定
课时安排
1
备课教师
时 间
教
学
目
标
1、了解不在同一条直线上的三个点确定一个圆,以及过不在同一条直线上的三个点作圆的方法,了解三角形外接圆,三角形的外心等概念。
2、经历不在同一条直线上三个点确定一个圆的探索过程,培养学生的探索能力。
3、 使学生初步掌握反证法的概念及反证法证题的基本方法。
教学重点
掌握过不在同一条直线上的三个点的作圆的方法;
三角形外接圆,三角形外心等的概念;
反证法证题的步骤。
教学难点
经历不在同一条直线上的三个点确定一个圆的探索过程,并能过不在同一条直线上的三个点画圆。
教学方法
教学资源
教学过程设计
教
学
过
程
教师活动
学生活动
修改意见
1.创设情境,导入新知
一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
先思考,然后小组讨论
2.知识回顾
过一点可以作几条直线?
过几点可以确定一条直线?
引入思考:
过几个点可以确定一个圆呢?
那么到底几个点可以确定一条直线呢?我们可以试一试。
1,2题集体回答,第三题思考之后回答
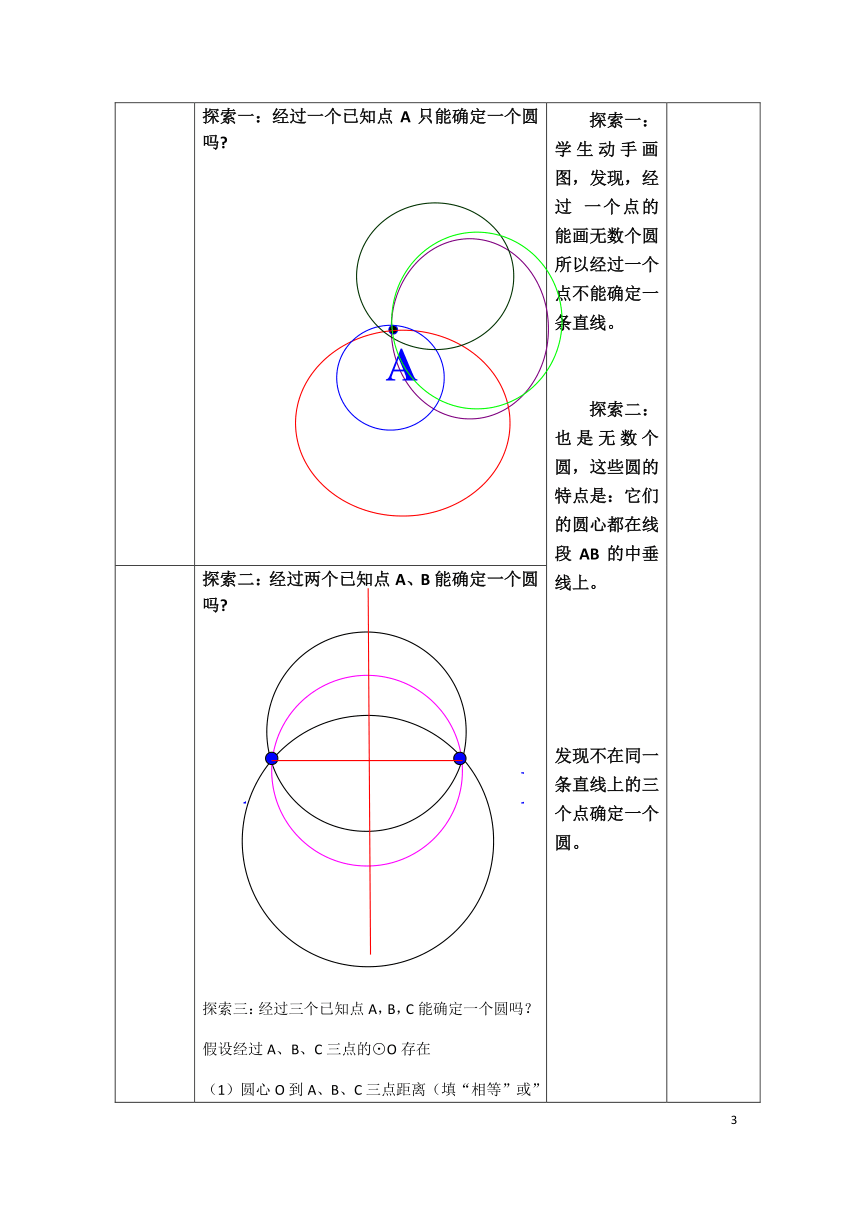
探索一:经过一个已知点A只能确定一个圆吗?
探索一:学生动手画图,发现,经过 一个点的能画无数个圆所以经过一个点不能确定一条直线。
探索二:也是无数个圆,这些圆的特点是:它们的圆心都在线段AB的中垂线上。
发现不在同一条直线上的三个点确定一个圆。
探索二:经过两个已知点A、B能确定一个圆吗?
探索三:经过三个已知点A,B,C能确定一个圆吗?
假设经过A、B、C三点的⊙O存在
圆心O到A、B、C三点距离(填“相等”或”不相等”)。
连结AB、AC,过O点 分别作直线MN⊥AB, EF⊥AC,则MN是AB的垂直平分线 ;EF是AC垂直平分线的。
AB、AC的中垂线的交点O到B、C的距离相等 。
思考:为什么在同一条直线上的三点不能确定圆?
画图:
已知:不在同一直线上的三点A、B、C
求作: ⊙O使它经过点A、B、C
作法:1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆。
现在你知道了怎样要将一个如图所示的破损的圆盘复原了吗?
方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OC长为半径作圆。
⊙O即为所求。
练一练:已知△ABC,用直尺和圆规作出过点A、B、C的圆
外接圆: 经过三角形各个顶点的圆叫做三角形的外接圆,外接圆 的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等。
练习
1.下列命题不正确的是
A.过一点有无数个圆. B.过两点有无数个圆.
C.弦是圆的一部分. D.过同一直线上三点不能画圆.
2.三角形的外心具有的性质是
A.到三边的距离相等. B.到三个顶点的距离相等.
C.外心在三角形的外. D.外心在三角形内.
3.判断
(1)经过三点一定可以作圆。( )
(2)三角形的外心就是这个三角形两边垂直平分线的交点。( )
(3)三角形的外心到三边的距离相等。( )
(4)等腰三角形的外心一定在这个三角形内。( )
本节课学习了哪些内容?
作业布置
教学反思
习题24.2
