沪科版九下:24.1 旋转 学案(2课时,无答案)
文档属性
| 名称 | 沪科版九下:24.1 旋转 学案(2课时,无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 112.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 22:07:36 | ||
图片预览

文档简介
旋转 学案
学习目标
1.通过具体实例认识旋转。
2.会找对应点、对应线段和对应角。
3.能按要求作出简单的平面图形旋转后的图形。
4.了解中心对称、中心对称图形的概念,探索它的基本性质。
5.认识和欣赏自然界和现实生活中的中心对称图形。
6.熟练地画出已知图形关于某一点成中心对称的图形。
学习重点
1.对生活中的旋转现象作数学上的分析、理解旋转的意义。
2.识别中心对称图形和成中心对称的两个图形的基本特征。
3.熟练地画出已知图形关于某一点成中心对称的图形。
学习难点
1.对旋转现象进行分析研究,旋转后的现象进行探索。
2.画出已知图形关于某一点成中心对称的图形。
学时安排
2学时
第一学时
学习过程
知识链接
在日常生活中,除了物体的平行移动外,我们还可以看到许多物体的旋转的现象:如时钟上的时针、分针、秒针在不停的转动。请你在列举一些有关旋转的现象。
(1)_______________________
(2)_______________________
(3)_______________________
学习内容
学法指导
学习反思
旋转的定义及相关概念:
旋转的三要素:
巩固概念,加深理解:
尝试运用:
阅读教材:
一、旋转定义
1.如图,单摆上小球的转动,由位置P转到位置P’,它是绕上面的悬挂点在一个平面上的转动,像这样的运动就叫做_______(rotation),这悬挂点就叫做小球旋转的___________(centre of roration)。
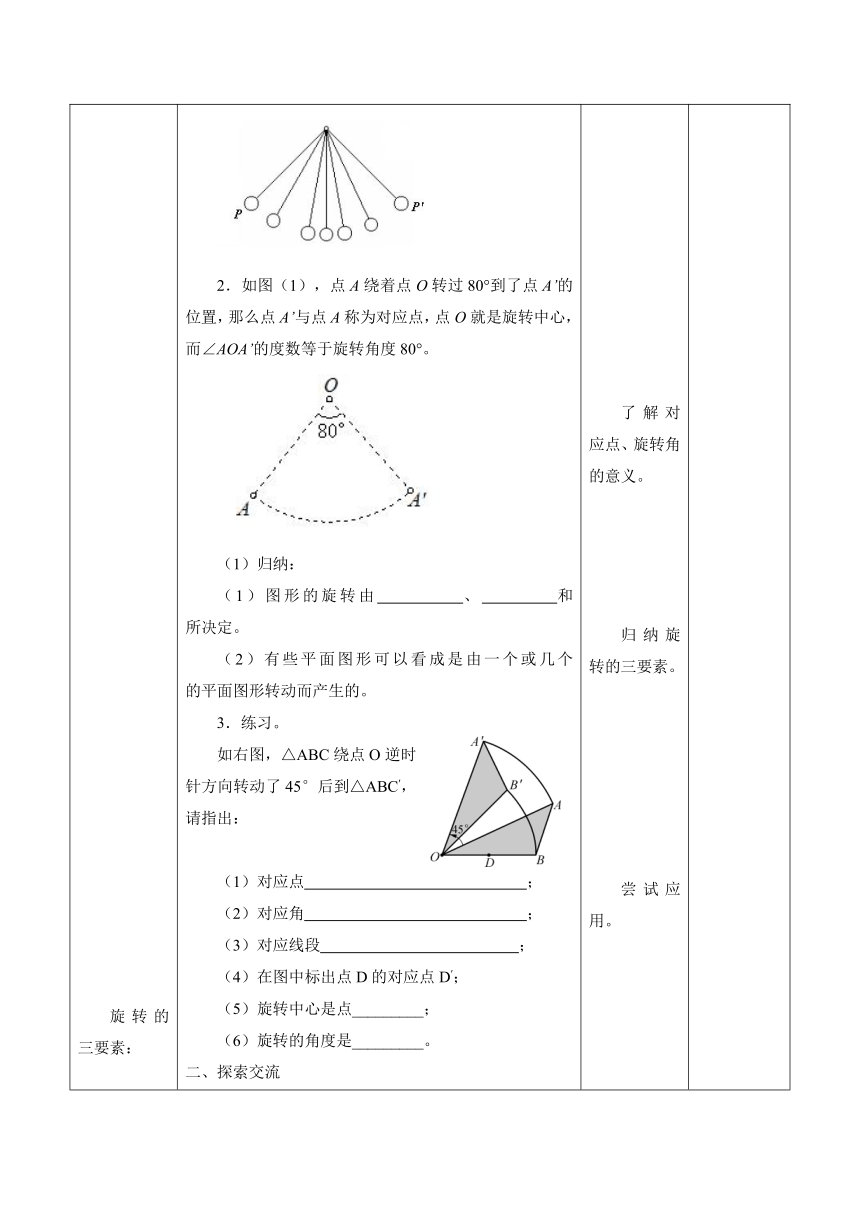
2.如图(1),点A绕着点O转过80°到了点A’的位置,那么点A’与点A称为对应点,点O就是旋转中心,而∠AOA’的度数等于旋转角度80°。
(1)归纳:
(1)图形的旋转由 、 和 所决定。
(2)有些平面图形可以看成是由一个或几个 的平面图形转动而产生的。
3.练习。
如右图,△ABC绕点O逆时针方向转动了45°后到△ABC′,请指出:
(1)对应点 ;
(2)对应角 ;
(3)对应线段 ;
(4)在图中标出点D的对应点D′;
(5)旋转中心是点_________;
(6)旋转的角度是_________。
二、探索交流
如右图,△ABC绕点O逆时针方向转动了60°后到△A′B′C,请指出:旋转中心、旋转角,并说明这两个三角形的顶点、边与角是如何对应的?
旋转中心:_______。
旋转角:___________________________。
对应顶点;_________________________。
对应边:___________________________。
对应角:___________________________。
三、实践应用
例1:如图,△ABC是等边三角形,D是BC边上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪个点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
解:
例2:点M是线段AB上一点,线段AB绕着点M顺时针方向旋转90°,旋转后的线段与原线段的位置有何关系?如果逆时针方向旋转90°呢?
解:
四、自我练习
教材课内练习。
填空
了解对应点、旋转角的意义。
归纳旋转的三要素。
尝试应用。
进一步深化理解概念。
尝试独立完成。
按要求完成。
学习小结
1.旋转的定义是:
_____________________________________。
2.旋转的三要素是______________。
3.旋转的性质:
自主归纳,形成体系。
第二学时
学习过程
一、自主学习
1.中心对称: 。
2.中心对称图形: 。
3.中心对称的特征: ;
。
4.如果两个图形的对应点连成的线段都经过某一点,并且被平分,那么这两个图形一定关于这一点成 。
5.给出下列图形:(1)角;(2)直角三角形;(3)等边三角形;(4)平行四边形(5)圆;(6)矩形;(7)正六边形;(8)正五边形;(9)正八边形;
是中心对称图形的是_______________。
6.如图,△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系?
7.中心对称与轴对称的联系与区别。
轴对称
中心对称
1
2
3
二、练习
1.如图所示,已知△ABC及其内部一点O,请画出与△ABC关于点O成中心对称的三角形。
2.如图所示的两个图形成中心对称,你能找到对称中心吗?
学习目标
1.通过具体实例认识旋转。
2.会找对应点、对应线段和对应角。
3.能按要求作出简单的平面图形旋转后的图形。
4.了解中心对称、中心对称图形的概念,探索它的基本性质。
5.认识和欣赏自然界和现实生活中的中心对称图形。
6.熟练地画出已知图形关于某一点成中心对称的图形。
学习重点
1.对生活中的旋转现象作数学上的分析、理解旋转的意义。
2.识别中心对称图形和成中心对称的两个图形的基本特征。
3.熟练地画出已知图形关于某一点成中心对称的图形。
学习难点
1.对旋转现象进行分析研究,旋转后的现象进行探索。
2.画出已知图形关于某一点成中心对称的图形。
学时安排
2学时
第一学时
学习过程
知识链接
在日常生活中,除了物体的平行移动外,我们还可以看到许多物体的旋转的现象:如时钟上的时针、分针、秒针在不停的转动。请你在列举一些有关旋转的现象。
(1)_______________________
(2)_______________________
(3)_______________________
学习内容
学法指导
学习反思
旋转的定义及相关概念:
旋转的三要素:
巩固概念,加深理解:
尝试运用:
阅读教材:
一、旋转定义
1.如图,单摆上小球的转动,由位置P转到位置P’,它是绕上面的悬挂点在一个平面上的转动,像这样的运动就叫做_______(rotation),这悬挂点就叫做小球旋转的___________(centre of roration)。
2.如图(1),点A绕着点O转过80°到了点A’的位置,那么点A’与点A称为对应点,点O就是旋转中心,而∠AOA’的度数等于旋转角度80°。
(1)归纳:
(1)图形的旋转由 、 和 所决定。
(2)有些平面图形可以看成是由一个或几个 的平面图形转动而产生的。
3.练习。
如右图,△ABC绕点O逆时针方向转动了45°后到△ABC′,请指出:
(1)对应点 ;
(2)对应角 ;
(3)对应线段 ;
(4)在图中标出点D的对应点D′;
(5)旋转中心是点_________;
(6)旋转的角度是_________。
二、探索交流
如右图,△ABC绕点O逆时针方向转动了60°后到△A′B′C,请指出:旋转中心、旋转角,并说明这两个三角形的顶点、边与角是如何对应的?
旋转中心:_______。
旋转角:___________________________。
对应顶点;_________________________。
对应边:___________________________。
对应角:___________________________。
三、实践应用
例1:如图,△ABC是等边三角形,D是BC边上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪个点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
解:
例2:点M是线段AB上一点,线段AB绕着点M顺时针方向旋转90°,旋转后的线段与原线段的位置有何关系?如果逆时针方向旋转90°呢?
解:
四、自我练习
教材课内练习。
填空
了解对应点、旋转角的意义。
归纳旋转的三要素。
尝试应用。
进一步深化理解概念。
尝试独立完成。
按要求完成。
学习小结
1.旋转的定义是:
_____________________________________。
2.旋转的三要素是______________。
3.旋转的性质:
自主归纳,形成体系。
第二学时
学习过程
一、自主学习
1.中心对称: 。
2.中心对称图形: 。
3.中心对称的特征: ;
。
4.如果两个图形的对应点连成的线段都经过某一点,并且被平分,那么这两个图形一定关于这一点成 。
5.给出下列图形:(1)角;(2)直角三角形;(3)等边三角形;(4)平行四边形(5)圆;(6)矩形;(7)正六边形;(8)正五边形;(9)正八边形;
是中心对称图形的是_______________。
6.如图,△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系?
7.中心对称与轴对称的联系与区别。
轴对称
中心对称
1
2
3
二、练习
1.如图所示,已知△ABC及其内部一点O,请画出与△ABC关于点O成中心对称的三角形。
2.如图所示的两个图形成中心对称,你能找到对称中心吗?
