苏科版七年级数学7.5多边形的内角和与外角和课时练习(含答案)
文档属性
| 名称 | 苏科版七年级数学7.5多边形的内角和与外角和课时练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 135.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-11 00:00:00 | ||
图片预览


文档简介
七年级数学7.5《多边形的内角和与外角和》课时练习
一、选择题:
1、若正多边形的一个外角是60°,则该正多边形的内角和为( )
A.360° B.540° C.720° D.900°
2、若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是( )
A.十三边形; B.十二边形; C.十一边形; D.十边形.
3、已知正多边形的一个外角等于40°,那么这个正多边形的边数为( )
A.6 B.7 C.8 D.9
4、一个多边形的内角和是720°,这个多边形的边数是( )
A.4 B.5 C.6 D.7
5、如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
A.140米 B.150米 C.160米 D.240米
6、将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )
A.360° B.540° C.720° D.900°
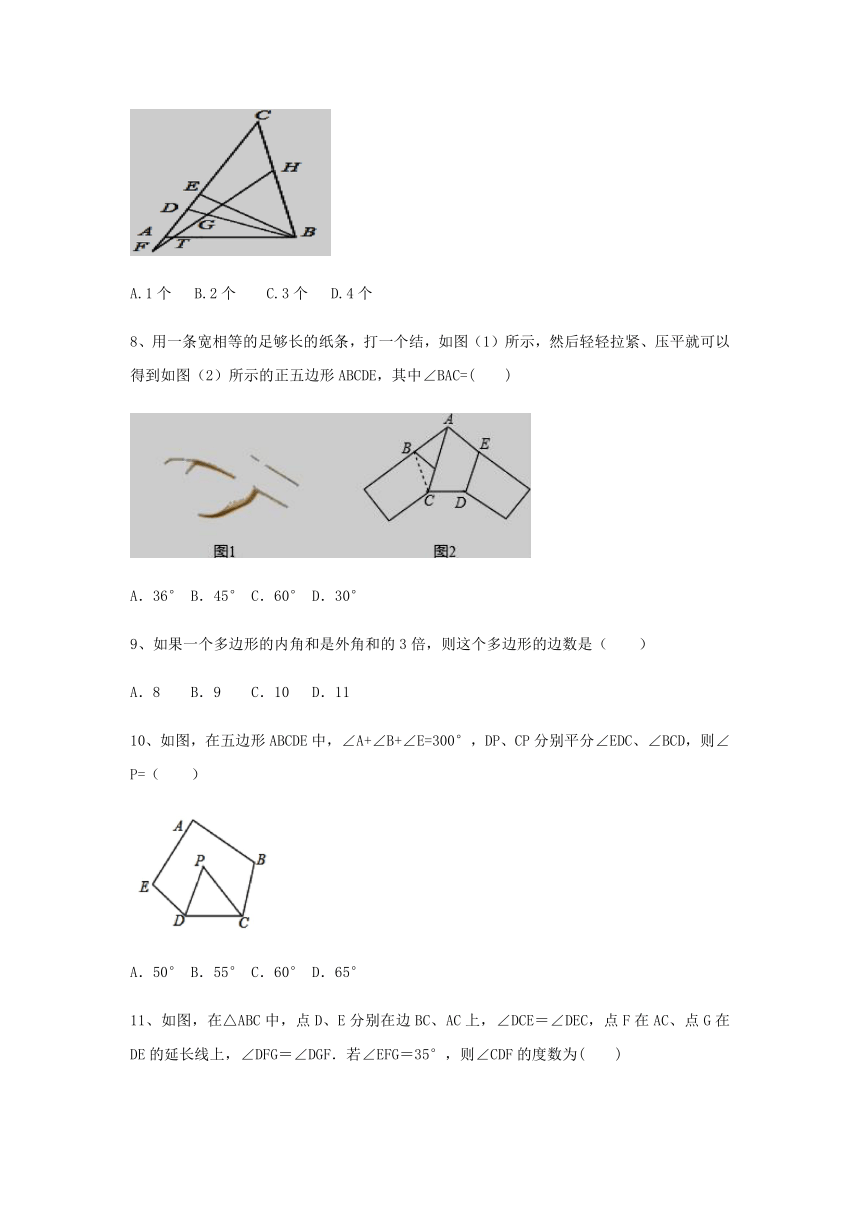
7、如图,在△ABC中,BD、BE分别是△ABC的高线和角平分线,点F在CA的延长线上,FH⊥BE交BD于点G,交BC于点H.下列结论:①∠DBE=∠F;②∠BEF=(∠BAF+∠C)/2; ③∠FGD=∠ABE+∠C;④∠F=(∠BAC﹣∠C)/2;其中正确的结论数量是 ( )
A.1个 B.2个 C.3个 D.4个
8、用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC=( )
A.36° B.45° C.60° D.30°
9、如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.8 B.9 C.10 D.11
10、如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P=( )
A.50° B.55° C.60° D.65°
11、如图,在△ABC中,点D、E分别在边BC、AC上,∠DCE=∠DEC,点F在AC、点G在DE的延长线上,∠DFG=∠DGF.若∠EFG=35°,则∠CDF的度数为( )
A.70° B.55° C.65° D.60°
12、如图所示,在四边形ABCD中,AD⊥AB,∠C=110°,它的一个外角∠ADE=60°,则∠B的大小是( )
A.50° B.45° C.40° D.60°
二、填空题:
13、正十边形的每一个内角的度数为 .
14、一个多边形的每一个外角都是36°,则这个多边形的边数是 .
15、若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是 .
16、若一个正多边形的内角和为720°,则这个正多边形的每一个内角是 .
17、一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为 .
18、通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是 度.
19、一个多边形的一个外角为α,且该多边形的内角和与α的和等于840°,则这个多边形的边数为 ,α= 度.
20、如果一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是 .
21、图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5= 度.
22、在△ABC中,∠ABC=100°,∠ACB=20°,CE平分∠ACB交AB于E,D在AC上,且∠CBD=20°,则∠CED的度数是 .
三、解答题:
23、如图,AC是正五边形ABCDE的一条对角线,求∠ACB的角度
24、如图,五边形ABCDE是正五边形.若l1∥l2,则∠1与∠2的差是多少度.
25、如图,∠1=∠2=∠3,且∠BAC=70°,∠DFE=50°,求∠ABC的度数.
26、小马虎同学在计算某个多边形的内角和时得到1840°,老师说他算错了,于是小马虎认真地检查了一遍
(1)若他检查发现其中一个内角多算了一次,求这个多边形的边数是多少?
(2)若他检查发现漏算了一个内角,求漏算的那个内角是多少度?这个多边形是几边形?
27、阅读材料:多边形上或内部的一点与多边形各顶点的连线,将多边形分割成若干个小三角形.图1给出了四边形的具体分割方法,分别将四边形分割成了2个,3个,4个小三角形.请你按照上述方法将图2中的六边形进行分割,并写出得到的小三角形的个数.试把这一结论推广至n边形.
参考答案
一、选择题:
1、 C 2、A 3、D 4、 C 5、B 6、D
7、D 8、 A 9、A 10、C 11、A 12、C
二、填空题:
13、144°
14、10
15、8
16、120°
17、7或8或9
18、540
19、3 120
20、540°或360°或180°
21、360
22、10°
三、解答题:
23、36°
24、72°
25、70°
26、(1)12 (2) 140° 13
27、第一种分割法,分割成的三角形的个数比边数少2,
第二种分割法分割成的三角形的个数比边数少1,
第三种分割法分割成的三角形的个数等于多边形的边数.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
