人教版六年级数学下册 第4单元 成反比例的量 课件(18张ppt)
文档属性
| 名称 | 人教版六年级数学下册 第4单元 成反比例的量 课件(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
2. 正比例和反比例
反比例
学习目标
1.通过感知生活中的事例,理解并掌握反比例的意义,能够初步判断两种相关联的量是否成反比例。
2.在解决实际问题的情境过程中,体会应用反比例知识解决实际问题的方法。
学习重点
理解反比例的意义。
学习难点
找出生活中成反比例的实例,能够判断两个量是否成反比例。
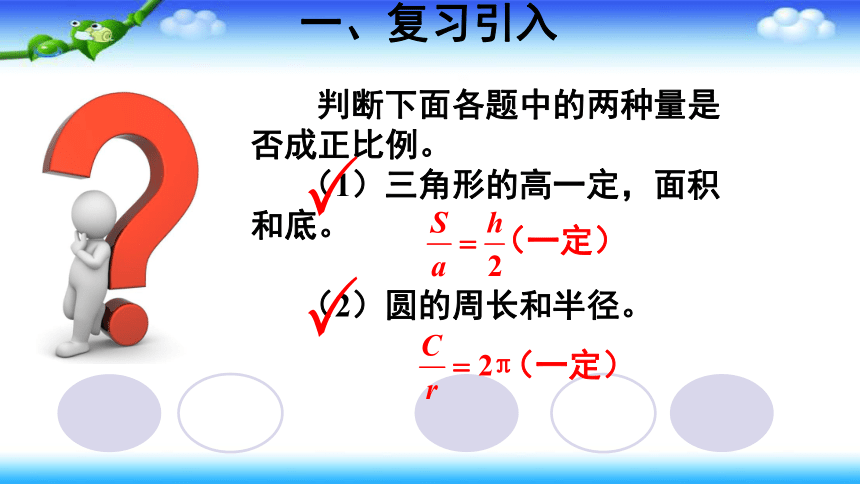
一、复习引入
判断下面各题中的两种量是否成正比例。
(1)三角形的高一定,面积和底。
(2)圆的周长和半径。
(一定)
(一定)
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm?
水的高度/cm
把相同体积的水倒入底面积不同的杯子。
反比例
10
30
15
20
20
15
30
10
60
5
…
…
二、探索新知
杯子的底面积/cm? 10 15 20 30 60 ...
水的高度/cm 30 20 15 10 5 ...
观察上表,回答下面的问题。
(1)表中有哪两种量?
(2)水的高度是怎样随着杯子底面积的大小变化而变化的?
水的高度随着杯子底面积的增大而减小。
杯子的底面积/cm? 10 15 20 30 60 ...
水的高度/cm 30 20 15 10 5 ...
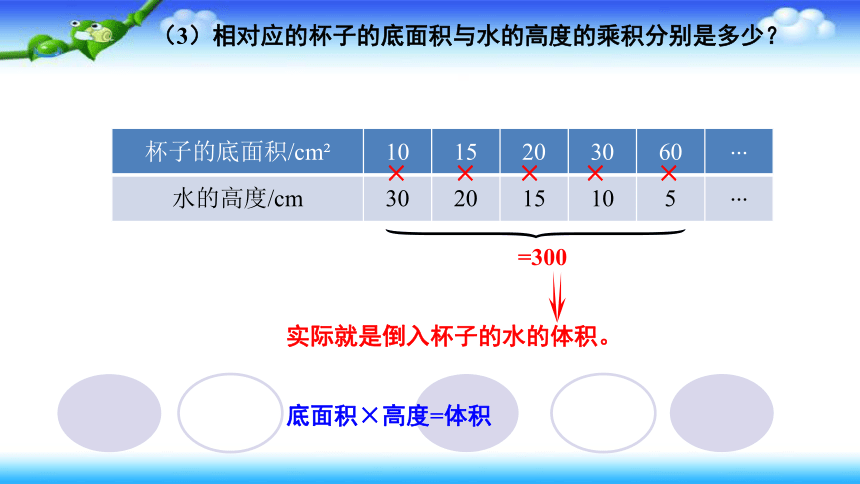
(3)相对应的杯子的底面积与水的高度的乘积分别是多少?
×
×
×
×
×
=300
实际就是倒入杯子的水的体积。
底面积×高度=体积
像这样两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定。这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用下面的式子表示:
x y=k
你能举出生活中反比例关系的例子吗?
如果总价一定,单价与数量成反比例关系。
如果长方形的面积一定,长与宽成反比例关系。
1.同学们做广播操,每行站的人数与站的行数的关系如下表。
每行站的人数 行数
10 60
12 50
15 40
20 30
三、随堂演练
每行站的人数与站的行数是否成反比例关系?为什么?
每行站的人数 行数
10 60
12 50
15 40
20 30
×
×
×
×
=600
每行站的人数与站的行数成反比例关系。
2.判断下面各题中的两种量是否成反比例。
(1)汽车的速度一定,行驶的路程和时间。
(2)非零自然数a和它的倒数。
(一定)
(a≠0)
成反比例
成正比例
四、巩固提高
做 一 做
(1)表中有哪两种量?它们是不是相关联的量?
每天运的吨数/t 300 150 100 75 60 50
运货的天数/天 1 2 3 4 5 6
是相关联的量
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说一说这个积表示什么?
每天运的吨数/t 300 150 100 75 60 50
运货的天数/天 1 2 3 4 5 6
300×1
150×2
100×3
=
=
=
300
货物的
总吨数
每天运的吨数/t 300 150 100 75 60 50
运货的天数/天 1 2 3 4 5 6
(3)运货的天数与每天运的吨数成反比例关系吗?为什么?
x
运货的天数
每天运的吨数
y
x×y=300
(一定)
成反比例关系
五、课堂小结
相关联的两种量x和y,如果它们的积k一定,则x和y叫做成反比例的量,它们的关系叫反比例关系。
x y=k
反比例
反比例关系表达式:
六、课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
1.学生已有了学习正比例的基础,正比例、反比例在研究意义的时候存在一定的共性。
2.正、反比例意义的对比,加强了知识的内在联系。通过区别不同的概念,巩固了知识。
3.从身边的现实生活中发掘素材,组织活动,让学生在活动中发现数学规律,激起学生自主参与的积极性和主动性。
七、教学反思
2. 正比例和反比例
反比例
学习目标
1.通过感知生活中的事例,理解并掌握反比例的意义,能够初步判断两种相关联的量是否成反比例。
2.在解决实际问题的情境过程中,体会应用反比例知识解决实际问题的方法。
学习重点
理解反比例的意义。
学习难点
找出生活中成反比例的实例,能够判断两个量是否成反比例。
一、复习引入
判断下面各题中的两种量是否成正比例。
(1)三角形的高一定,面积和底。
(2)圆的周长和半径。
(一定)
(一定)
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm?
水的高度/cm
把相同体积的水倒入底面积不同的杯子。
反比例
10
30
15
20
20
15
30
10
60
5
…
…
二、探索新知
杯子的底面积/cm? 10 15 20 30 60 ...
水的高度/cm 30 20 15 10 5 ...
观察上表,回答下面的问题。
(1)表中有哪两种量?
(2)水的高度是怎样随着杯子底面积的大小变化而变化的?
水的高度随着杯子底面积的增大而减小。
杯子的底面积/cm? 10 15 20 30 60 ...
水的高度/cm 30 20 15 10 5 ...
(3)相对应的杯子的底面积与水的高度的乘积分别是多少?
×
×
×
×
×
=300
实际就是倒入杯子的水的体积。
底面积×高度=体积
像这样两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定。这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用下面的式子表示:
x y=k
你能举出生活中反比例关系的例子吗?
如果总价一定,单价与数量成反比例关系。
如果长方形的面积一定,长与宽成反比例关系。
1.同学们做广播操,每行站的人数与站的行数的关系如下表。
每行站的人数 行数
10 60
12 50
15 40
20 30
三、随堂演练
每行站的人数与站的行数是否成反比例关系?为什么?
每行站的人数 行数
10 60
12 50
15 40
20 30
×
×
×
×
=600
每行站的人数与站的行数成反比例关系。
2.判断下面各题中的两种量是否成反比例。
(1)汽车的速度一定,行驶的路程和时间。
(2)非零自然数a和它的倒数。
(一定)
(a≠0)
成反比例
成正比例
四、巩固提高
做 一 做
(1)表中有哪两种量?它们是不是相关联的量?
每天运的吨数/t 300 150 100 75 60 50
运货的天数/天 1 2 3 4 5 6
是相关联的量
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说一说这个积表示什么?
每天运的吨数/t 300 150 100 75 60 50
运货的天数/天 1 2 3 4 5 6
300×1
150×2
100×3
=
=
=
300
货物的
总吨数
每天运的吨数/t 300 150 100 75 60 50
运货的天数/天 1 2 3 4 5 6
(3)运货的天数与每天运的吨数成反比例关系吗?为什么?
x
运货的天数
每天运的吨数
y
x×y=300
(一定)
成反比例关系
五、课堂小结
相关联的两种量x和y,如果它们的积k一定,则x和y叫做成反比例的量,它们的关系叫反比例关系。
x y=k
反比例
反比例关系表达式:
六、课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
1.学生已有了学习正比例的基础,正比例、反比例在研究意义的时候存在一定的共性。
2.正、反比例意义的对比,加强了知识的内在联系。通过区别不同的概念,巩固了知识。
3.从身边的现实生活中发掘素材,组织活动,让学生在活动中发现数学规律,激起学生自主参与的积极性和主动性。
七、教学反思
