华师大版九年级数学下册:27.1.2 圆的对称性 同步练习 (解析版)
文档属性
| 名称 | 华师大版九年级数学下册:27.1.2 圆的对称性 同步练习 (解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 507.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 00:00:00 | ||
图片预览


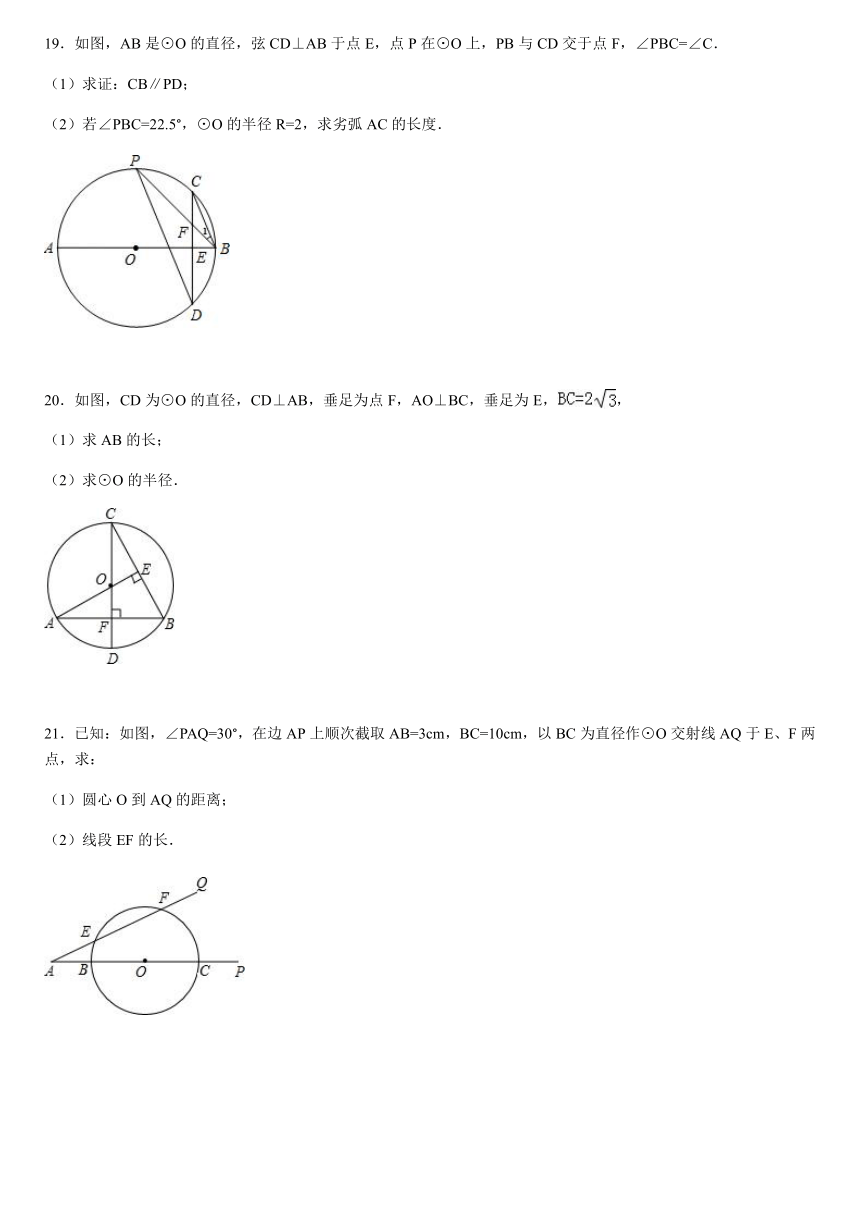
文档简介
27.1.2圆的对称性
一.选择题(共8小题)
1.在同圆或等圆中,下列说法错误的是( )
A.相等弦所对的弧相等 B.相等弦所对的圆心角相等
C.相等圆心角所对的弧相等 D.相等圆心角所对的弦相等
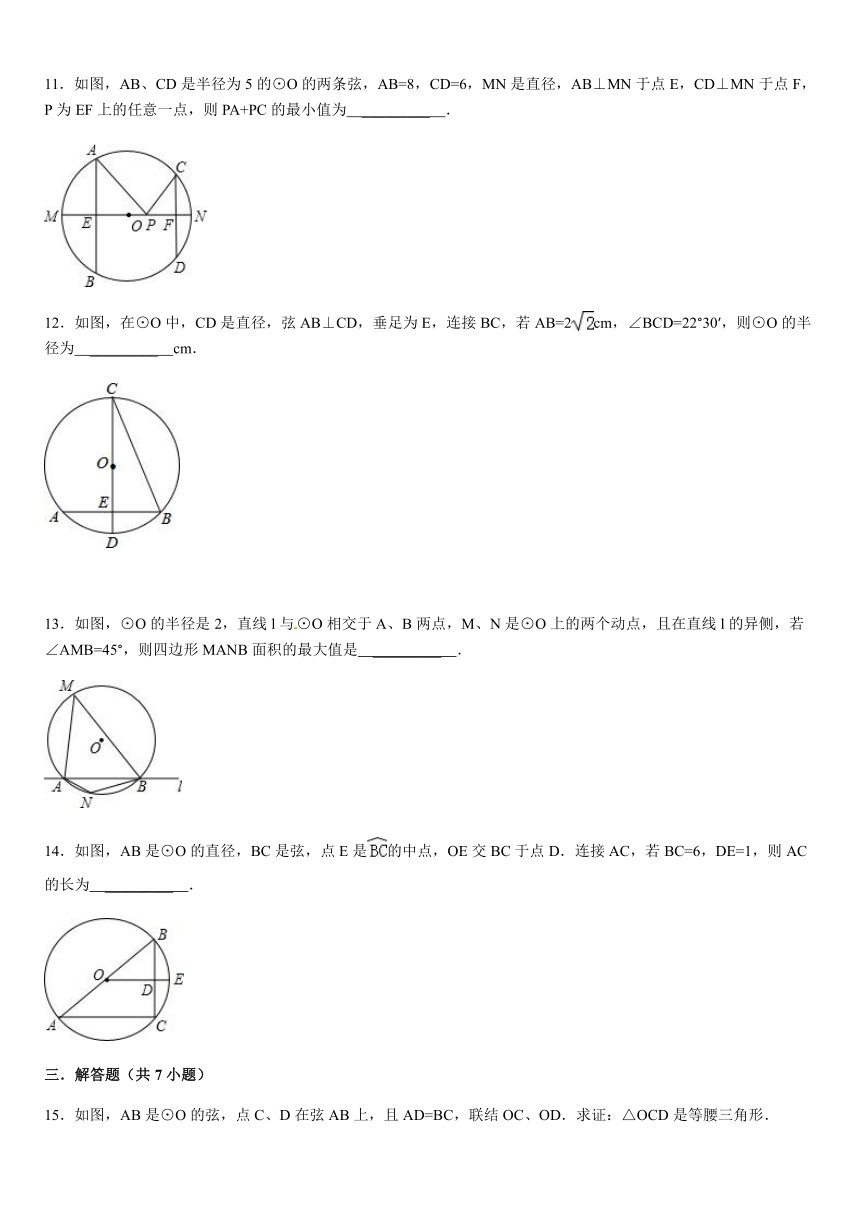
2.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A.6 B.5 C.4 D.3
3.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )
A.cm B.cm C.cm或cm D.cm或cm
4.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则AB的长为( )
A.2 B.4 C.6 D.8
5.如图,CD是⊙O的直径,弦AB⊥CD于E,连接BC、BD,下列结论中不一定正确的是( )
A.AE=BE B.= C.OE=DE D.∠DBC=90°
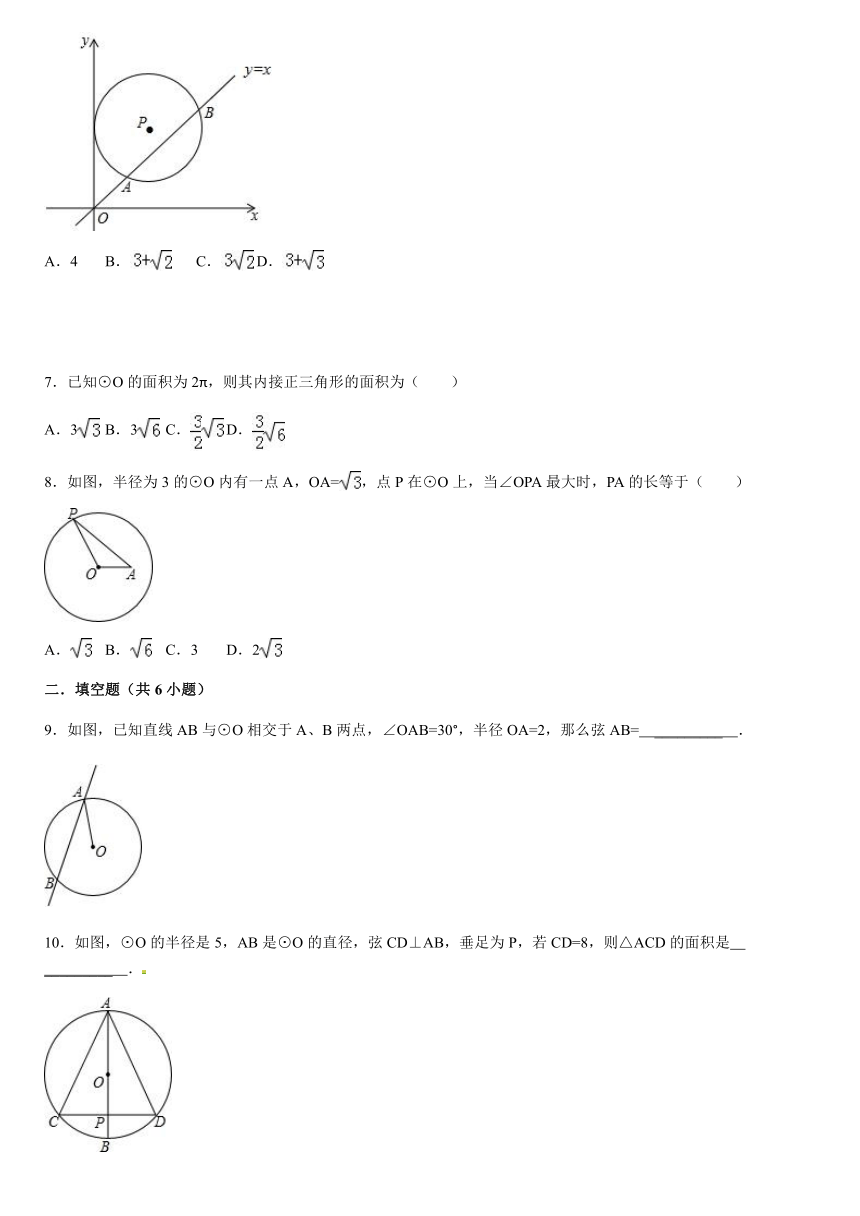
6.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是( )
A.4 B. C. D.
7.已知⊙O的面积为2π,则其内接正三角形的面积为( )
A.3 B.3 C. D.
8.如图,半径为3的⊙O内有一点A,OA=,点P在⊙O上,当∠OPA最大时,PA的长等于( )
A. B. C.3 D.2
二.填空题(共6小题)
9.如图,已知直线AB与⊙O相交于A、B两点,∠OAB=30°,半径OA=2,那么弦AB= _________ .
10.如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是 _________ .
11.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 _________ .
12.如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2cm,∠BCD=22°30′,则⊙O的半径为 _________ cm.
13.如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是 _________ .
14.如图,AB是⊙O的直径,BC是弦,点E是的中点,OE交BC于点D.连接AC,若BC=6,DE=1,则AC的长为 _________ .
三.解答题(共7小题)
15.如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形.
16.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
17.如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.
18.如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
19.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
(1)求证:CB∥PD;
(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.
20.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为E,,
(1)求AB的长;
(2)求⊙O的半径.
21.已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:
(1)圆心O到AQ的距离;
(2)线段EF的长.
27.1.2圆的对称性1
参考答案与试题解析
一.选择题(共8小题)
1.在同圆或等圆中,下列说法错误的是( )
A. 相等弦所对的弧相等 B.相等弦所对的圆心角相等
C. 相等圆心角所对的弧相等 D. 相等圆心角所对的弦相等
考点: 圆心角、弧、弦的关系.
分析: 利用在同圆和等圆中,相等的弦所对的圆心角相等,相等的圆心角所对的弧相等,所对的弦也相等,判断出B、C、D三选项都正确;而同圆或等圆中,同一条弦对应两条弧,其中一条是优弧,一条是劣弧,所以可判断出A选项错误.
解答:解:A、相等弦所对的弧不一定相等,故本选项错误;
B、相等弦所对的圆心角相等,故本选项正确;
C、相等圆心角所对的弧相等,故本选项正确;
D、相等圆心角所对的弦相等,故本选项正确.
故选A.
点评:此题考查了圆心角、弧、弦的关系定理的推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.注意:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本推论中的“弧”是指同为优弧或劣弧.
2.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A. 6 B.5 C.4 D. 3
考点: 垂径定理;勾股定理.
分析: 过O作OC⊥AB于C,根据垂径定理求出AC,根据勾股定理求出OC即可.
解答:解:过O作OC⊥AB于C,
∵OC过O,
∴AC=BC=AB=12,
在Rt△AOC中,由勾股定理得:OC==5.
故选:B.
点评:本题考查了垂径定理和勾股定理的应用,关键是求出OC的长.
3.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )
A. cm B.cm C.cm或cm D. cm或cm
考点: 垂径定理;勾股定理.
专题: 分类讨论.
分析: 先根据题意画出图形,由于点C的位置不能确定,故应分两种情况进行讨论.
解答: 解:连接AC,AO,
∵⊙O的直径CD=10cm,AB⊥CD,AB=8cm,
∴AM=AB=×8=4cm,OD=OC=5cm,
当C点位置如图1所示时,
∵OA=5cm,AM=4cm,CD⊥AB,
∴OM===3cm,
∴CM=OC+OM=5+3=8cm,
∴AC===4cm;
当C点位置如图2所示时,同理可得OM=3cm,
∵OC=5cm,
∴MC=5﹣3=2cm,
在Rt△AMC中,AC===2cm.
故选:C.
点评: 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
4.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则AB的长为( )
A. 2 B.4 C.6 D.8
考点: 垂径定理;勾股定理.
专题: 计算题.
分析: 根据CE=2,DE=8,得出半径为5,在直角三角形OBE中,由勾股定理得BE,根据垂径定理得出AB的长.
解答: 解:∵CE=2,DE=8,
∴OB=5,
∴OE=3,
∵AB⊥CD,
∴在△OBE中,得BE=4,
∴AB=2BE=8.
故选:D.
点评本题考查了勾股定理以及垂径定理,是基础知识要熟练掌握.
5.如图,CD是⊙O的直径,弦AB⊥CD于E,连接BC、BD,下列结论中不一定正确的是( )
A. AE=BE B.= C.OE=DE D. ∠DBC=90°
考点: 垂径定理;圆周角定理.
专题: 几何图形问题.
分析: 由于CD⊥AB,根据垂径定理有AE=BE,弧AD=弧BD,不能得出OE=DE,直径所对的圆周角等于90°.
解答: 解:∵CD⊥AB,
∴AE=BE,=,
∵CD是⊙O的直径,
∴∠DBC=90°,
不能得出OE=DE.
故选:C.
点评: 本题考查了垂径定理.解题的关键是熟练掌握垂径定理的内容.
6.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是( )
A. 4 B. C. D.
考点:垂径定理;一次函数图象上点的坐标特征;勾股定理.
专题:计算题;压轴题.
分析: PC⊥x轴于C,交AB于D,作PE⊥AB于E,连结PB,由于OC=3,PC=a,易得D点坐标为(3,3),则△OCD为等腰直角三角形,△PED也为等腰直角三角形.由PE⊥AB,根据垂径定理得AE=BE=AB=2,在Rt△PBE中,利用勾股定理可计算出PE=1,则PD=PE=,所以a=3+.
解答: 解:作PC⊥x轴于C,交AB于D,作PE⊥AB于E,连结PB,如图,
∵⊙P的圆心坐标是(3,a),
∴OC=3,PC=a,
把x=3代入y=x得y=3,
∴D点坐标为(3,3),
∴CD=3,
∴△OCD为等腰直角三角形,
∴△PED也为等腰直角三角形,
∵PE⊥AB,
∴AE=BE=AB=×4=2,
在Rt△PBE中,PB=3,
∴PE=,
∴PD=PE=,
∴a=3+.
故选:B.
点评: 本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理和等腰直角三角形的性质.
7.已知⊙O的面积为2π,则其内接正三角形的面积为( )
A. 3 B.3 C. D.
考点: 垂径定理;等边三角形的性质.
专题: 几何图形问题.
分析: 先求出正三角形的外接圆的半径,再求出正三角形的边长,最后求其面积即可.
解答: 解:如图所示,
连接OB、OC,过O作OD⊥BC于D,
∵⊙O的面积为2π
∴⊙O的半径为
∵△ABC为正三角形,
∴∠BOC==120°,∠BOD=∠BOC=60°,OB=,
∴BD=OB?sin∠BOD==,
∴BC=2BD=,
∴OD=OB?cos∠BOD=?cos60°=,
∴△BOC的面积=?BC?OD=××=,
∴△ABC的面积=3S△BOC=3×=.
故选:C.
点评: 本题考查的是三角形的外接圆与外心,根据题意画出图形,利用数形结合求解是解答此题的关键.
8.如图,半径为3的⊙O内有一点A,OA=,点P在⊙O上,当∠OPA最大时,PA的长等于( )
A. B. C.3 D. 2
考点: 垂径定理;圆周角定理.
分析: 当PA⊥OA时,PA取最小值,∠OPA取得最大值,然后在直角三角形OPA中利用勾股定理求PA的值即可.
解答: 解:∵OA、OP是定值,
∴在△OPA中,当∠OPA取最大值时,PA取最小值,
∴PA⊥OA时,PA取最小值;
在直角三角形OPA中,OA=,OP=3,
∴PA==.
故选B.
点评: 本题考查了解直角三角形.解答此题的关键是找出“当PA⊥OA时,PA取最小值”即“PA⊥OA时,∠OPA取最大值”这一隐含条件.
二.填空题(共6小题)
9.如图,已知直线AB与⊙O相交于A、B两点,∠OAB=30°,半径OA=2,那么弦AB= 2 .
考点: 垂径定理;含30度角的直角三角形;勾股定理.
分析: 过O作OC⊥AB于C,根据垂直和垂径定理求出AB=2AC,∠OCA=90°,根据含30度角的直角三角形性质求出OC=1,根据勾股定理求出AC,即可得出答案.
解答: 解:
过O作OC⊥AB于C,
则AB=2AC,∠OCA=90°,
∵OA=2,∠OAB=30°,
∴OC=1,由勾股定理得:AC==,
∴AB=2AC=2,
故答案为:2.
点评: 本题考查了垂径定理,含30度角的直角三角形性质,勾股定理的应用,解此题的关键是正确作出辅助线后求出AC的长和得出AB=2AC,注意:垂直于弦的直径平分这条弦.
10.如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是 32 .
考点: 垂径定理;勾股定理.
分析: 连接OD,先根据垂径定理得出PD=CD=4,再根据勾股定理求出OP的长,根据三角形的面积公式即可得出结论.
解答: 解:连接OD,
∵⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,CD=8,
∴PD=CD=4,
∴OP===3,
∴AP=OA+OP=5+3=8,
∴S△ACD=CD?AP=×8×8=32.
故答案为:32.
点评: 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
11.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .
考点: 垂径定理;轴对称的性质.
分析: A、B两点关于MN对称,因而PA+PC=PB+PC,即当B、C、P在一条直线上时,PA+PC的最小,即BC的值就是PA+PC的最小值
解答: 解:连接OA,OB,OC,作CH垂直于AB于H.
根据垂径定理,得到BE=AB=4,CF=CD=3,
∴OE===3,
OF===4,
∴CH=OE+OF=3+4=7,
BH=BE+EH=BE+CF=4+3=7,
在直角△BCH中根据勾股定理得到BC=7,
则PA+PC的最小值为.
故答案为:
点评: 正确理解BC的长是PA+PC的最小值,是解决本题的关键.
12.如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2cm,∠BCD=22°30′,则⊙O的半径为 2 cm.
考点: 垂径定理;等腰直角三角形;圆周角定理.
专题: 计算题.
分析: 先根据圆周角定理得到∠BOD=2∠BCD=45°,再根据垂径定理得到BE=AB=,且△BOE为等腰直角三角形,然后根据等腰直角三角形的性质求解.
解答: 解:连结OB,如图,
∵∠BCD=22°30′,
∴∠BOD=2∠BCD=45°,
∵AB⊥CD,
∴BE=AE=AB=×2=,△BOE为等腰直角三角形,
∴OB=BE=2(cm).
故答案为:2.
点评: 本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了等腰直角三角形的性质和圆周角定理.
13.如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是 4 .
考点: 垂径定理;圆周角定理.
专题: 计算题.
分析: 过点O作OC⊥AB于C,交⊙O于D、E两点,连结OA、OB、DA、DB、EA、EB,根据圆周角定理得∠AOB=2∠AMB=90°,则△OAB为等腰直角三角形,所以AB=OA=2,由于S四边形MANB=S△MAB+S△NAB,而当M点到AB的距离最大,△MAB的面积最大;当N点到AB的距离最大时,△NAB的面积最大,即M点运动到D点,N点运动到E点,所以四边形MANB面积的最大值=S四边形DAEB=S△DAB+S△EAB=AB?CD+AB?CE=AB(CD+CE)=AB?DE=×2×4=4.
解答: 解:过点O作OC⊥AB于C,交⊙O于D、E两点,连结OA、OB、DA、DB、EA、EB,如图,
∵∠AMB=45°,
∴∠AOB=2∠AMB=90°,
∴△OAB为等腰直角三角形,
∴AB=OA=2,
∵S四边形MANB=S△MAB+S△NAB,
∴当M点到AB的距离最大,△MAB的面积最大;当N点到AB的距离最大时,△NAB的面积最大,
即M点运动到D点,N点运动到E点,
此时四边形MANB面积的最大值=S四边形DAEB=S△DAB+S△EAB=AB?CD+AB?CE=AB(CD+CE)=AB?DE=×2×4=4.
故答案为:4.
点评: 本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理.
14.如图,AB是⊙O的直径,BC是弦,点E是的中点,OE交BC于点D.连接AC,若BC=6,DE=1,则AC的长为 8 .
考点: 垂径定理;勾股定理;三角形中位线定理.
专题: 计算题.
分析: 连接OC,根据圆心角与弧之间的关系可得∠BOE=∠COE,由于OB=OC,根据等腰三角形的性质可得OD⊥BC,BD=CD.在直角三角形BDO中,根据勾股定理可求出OB,进而求出OD长,再根据三角形中位线定理可得AC的长.
解答: 解:连接OC,如图所示.
∵点E是的中点,
∴∠BOE=∠COE.
∵OB=OC,
∴OD⊥BC,BD=DC.
∵BC=6,
∴BD=3.
设⊙O的半径为r,则OB=OE=r.
∵DE=1,
∴OD=r﹣1.
∵OD⊥BC即∠BDO=90°,
∴OB2=BD2+OD2.
∵OB=r,OD=r﹣1,BD=3,
∴r2=32+(r﹣1)2.
解得:r=5.
∴OD=4.
∵AO=BO,BD=CD,
∴OD=AC.
∴AC=8.
点评: 本题考查了在同圆或等圆中等弧所对的圆心角相等、等腰三角形的性质、勾股定理、三角形中位线定理等知识,有一定的综合性.
三.解答题(共7小题)
15.如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形.
考点: 垂径定理;等腰三角形的判定.
专题: 证明题.
分析: 过O作OE⊥AB于E,根据垂径定理求出AE=BE,求出CE=DE,根据线段垂直平分线性质求出OD=OC,即可得出答案.
解答: 证明:
过O作OE⊥AB于E,
则AE=BE,
∵AD=BC,
∴AD﹣DC=BC﹣DC,
∴AC=DE,
∴CE=DE,
∵OE⊥CD,
∴OC=OD,
即△OCD是等腰三角形.
点评: 本题考查了垂径定理,等腰三角形的判定,线段垂直平分线性质的应用,解此题的关键是正确作出辅助线后求出CE=DE.
16.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
考点: 垂径定理;勾股定理.
专题: 几何综合题.
分析: (1)过O作OE⊥AB,根据垂径定理得到AE=BE,CE=DE,从而得到AC=BD;
(2)由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,再根据勾股定理求出CE及AE的长,根据AC=AE﹣CE即可得出结论.
解答: (1)证明:过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE﹣DE=AE﹣CE,即AC=BD;
(2)解:由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,
∴OE=6,
∴CE===2,AE===8,
∴AC=AE﹣CE=8﹣2.
点评: 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
17.如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.
考点: 垂径定理;勾股定理;圆周角定理.
专题: 几何综合题.
分析: (1)先根据CD=16,BE=4,得出OE的长,进而得出OB的长,进而得出结论;
(2)由∠M=∠D,∠DOB=2∠D,结合直角三角形可以求得结果;
解答: 解:(1)∵AB⊥CD,CD=16,
∴CE=DE=8,
设OB=x,
又∵BE=4,
∴x2=(x﹣4)2+82,
解得:x=10,
∴⊙O的直径是20.
(2)∵∠M=∠BOD,∠M=∠D,
∴∠D=∠BOD,
∵AB⊥CD,
∴∠D=30°.
点评: 本题考查了圆的综合题:在同圆或等圆中,相等的弧所对的圆周角相等,直径所对的圆周角为直角;垂直于弦的直径平分弦,并且平分弦所对的弧;
18.如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
考点: 垂径定理;勾股定理.
专题: 几何图形问题.
分析: 过点O作OE⊥AB于点E,连接OB,由垂径定理可知AE=BE=AB,再根据勾股定理求出OE的长,由此可得出结论.
解答: 解:过点O作OE⊥AB于点E,连接OB,
∵AB=8cm,
∴AE=BE=AB=×8=4cm,
∵⊙O的直径为10cm,
∴OB=×10=5cm,
∴OE===3cm,
∵垂线段最短,半径最长,
∴3cm≤OP≤5cm.
点评: 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
19.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
(1)求证:CB∥PD;
(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.
考点: 垂径定理;圆周角定理;弧长的计算.
专题: 几何图形问题.
分析: (1)先根据同弧所对的圆周角相等得出∠PBC=∠D,再由等量代换得出∠C=∠D,然后根据内错角相等两直线平行即可证明CB∥PD;
(2)先由垂径定理及圆周角定理得出∠BOC=2∠PBC=45°,再根据邻补角定义求出∠AOC=135°,然后根据弧长的计算公式即可得出劣弧AC的长度.
解答: 解:(1)∵∠PBC=∠D,∠PBC=∠C,
∴∠C=∠D,
∴CB∥PD;
(2)连结OC,OD.
∵AB是⊙O的直径,弦CD⊥AB于点E,
∴=,
∵∠PBC=∠C=22.5°,
∴∠BOC=∠BOD=2∠C=45°,
∴∠AOC=180°﹣∠BOC=135°,
∴劣弧AC的长为:=.
点评: 本题考查了圆周角定理,平行线的判定,垂径定理,弧长的计算,难度适中.(2)中求出∠AOC=135°是解题的关键.
20.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为E,,
(1)求AB的长;
(2)求⊙O的半径.
考点: 垂径定理;等边三角形的判定与性质.
分析: (1)先根据CD为⊙O的直径,CD⊥AB得出=,故可得出∠C=∠AOD,由对顶角相等得出∠AOD=∠COE,故可得出∠C=∠COE,再根据AO⊥BC可知∠AEC=90°,故∠C=30°,再由直角三角形的性质可得出BF的长,进而得出结论;
(2)在Rt△OCE中根据∠C=30°即可得出OC的长.
解答: 解:(1)∵CD为⊙O的直径,CD⊥AB,
∴=,AF=BF,
∴∠C=∠AOD,
∵∠AOD=∠COE,
∴∠C=∠COE,
∵AO⊥BC,
∴∠AEC=90°,
∴∠C=30°,
∵BC=2,
∴BF=BC=,
∴AB=2BF=2;
(2)∵AO⊥BC,BC=2,
∴CE=BE=BC=,
∵∠C=30°,
∴OC===2,即⊙O的半径是2.
点评: 本题考查的是垂径定理,熟知“平分弦的直径平分这条弦,并且平分弦所对的两条弧”是解答此题的关键.
21.已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:
(1)圆心O到AQ的距离;
(2)线段EF的长.
考点: 垂径定理;含30度角的直角三角形;勾股定理.
分析: (1)过点O作OH⊥EF,垂足为点H,求出AO,根据含30度角的直角三角形性质求出即可;
(2)连接OE,根据勾股定理求出EH,根据垂径定理得出即可.
解答: 解:(1)过点O作OH⊥EF,垂足为点H,
∵OH⊥EF,
∴∠AHO=90°,
在Rt△AOH中,∵∠AHO=90°,∠PAQ=30°,
∴OH=AO,
∵BC=10cm,
∴BO=5cm.
∵AO=AB+BO,AB=3cm,
∴AO=3+5=8cm,
∴OH=4cm,即圆心O到AQ的距离为4cm.
(2)连接OE,
在Rt△EOH中,
∵∠EHO=90°,∴EH2+HO2=EO2,
∵EO=5cm,OH=4cm,
∴EH===3cm,
∵OH过圆心O,OH⊥EF,
∴EF=2EH=6cm.
点评: 本题考查了含30度角的直角三角形性质,勾股定理,垂径定理的应用,题目是一道比较典型的题目,难度适中.
一.选择题(共8小题)
1.在同圆或等圆中,下列说法错误的是( )
A.相等弦所对的弧相等 B.相等弦所对的圆心角相等
C.相等圆心角所对的弧相等 D.相等圆心角所对的弦相等
2.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A.6 B.5 C.4 D.3
3.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )
A.cm B.cm C.cm或cm D.cm或cm
4.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则AB的长为( )
A.2 B.4 C.6 D.8
5.如图,CD是⊙O的直径,弦AB⊥CD于E,连接BC、BD,下列结论中不一定正确的是( )
A.AE=BE B.= C.OE=DE D.∠DBC=90°
6.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是( )
A.4 B. C. D.
7.已知⊙O的面积为2π,则其内接正三角形的面积为( )
A.3 B.3 C. D.
8.如图,半径为3的⊙O内有一点A,OA=,点P在⊙O上,当∠OPA最大时,PA的长等于( )
A. B. C.3 D.2
二.填空题(共6小题)
9.如图,已知直线AB与⊙O相交于A、B两点,∠OAB=30°,半径OA=2,那么弦AB= _________ .
10.如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是 _________ .
11.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 _________ .
12.如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2cm,∠BCD=22°30′,则⊙O的半径为 _________ cm.
13.如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是 _________ .
14.如图,AB是⊙O的直径,BC是弦,点E是的中点,OE交BC于点D.连接AC,若BC=6,DE=1,则AC的长为 _________ .
三.解答题(共7小题)
15.如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形.
16.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
17.如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.
18.如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
19.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
(1)求证:CB∥PD;
(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.
20.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为E,,
(1)求AB的长;
(2)求⊙O的半径.
21.已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:
(1)圆心O到AQ的距离;
(2)线段EF的长.
27.1.2圆的对称性1
参考答案与试题解析
一.选择题(共8小题)
1.在同圆或等圆中,下列说法错误的是( )
A. 相等弦所对的弧相等 B.相等弦所对的圆心角相等
C. 相等圆心角所对的弧相等 D. 相等圆心角所对的弦相等
考点: 圆心角、弧、弦的关系.
分析: 利用在同圆和等圆中,相等的弦所对的圆心角相等,相等的圆心角所对的弧相等,所对的弦也相等,判断出B、C、D三选项都正确;而同圆或等圆中,同一条弦对应两条弧,其中一条是优弧,一条是劣弧,所以可判断出A选项错误.
解答:解:A、相等弦所对的弧不一定相等,故本选项错误;
B、相等弦所对的圆心角相等,故本选项正确;
C、相等圆心角所对的弧相等,故本选项正确;
D、相等圆心角所对的弦相等,故本选项正确.
故选A.
点评:此题考查了圆心角、弧、弦的关系定理的推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.注意:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本推论中的“弧”是指同为优弧或劣弧.
2.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A. 6 B.5 C.4 D. 3
考点: 垂径定理;勾股定理.
分析: 过O作OC⊥AB于C,根据垂径定理求出AC,根据勾股定理求出OC即可.
解答:解:过O作OC⊥AB于C,
∵OC过O,
∴AC=BC=AB=12,
在Rt△AOC中,由勾股定理得:OC==5.
故选:B.
点评:本题考查了垂径定理和勾股定理的应用,关键是求出OC的长.
3.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )
A. cm B.cm C.cm或cm D. cm或cm
考点: 垂径定理;勾股定理.
专题: 分类讨论.
分析: 先根据题意画出图形,由于点C的位置不能确定,故应分两种情况进行讨论.
解答: 解:连接AC,AO,
∵⊙O的直径CD=10cm,AB⊥CD,AB=8cm,
∴AM=AB=×8=4cm,OD=OC=5cm,
当C点位置如图1所示时,
∵OA=5cm,AM=4cm,CD⊥AB,
∴OM===3cm,
∴CM=OC+OM=5+3=8cm,
∴AC===4cm;
当C点位置如图2所示时,同理可得OM=3cm,
∵OC=5cm,
∴MC=5﹣3=2cm,
在Rt△AMC中,AC===2cm.
故选:C.
点评: 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
4.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则AB的长为( )
A. 2 B.4 C.6 D.8
考点: 垂径定理;勾股定理.
专题: 计算题.
分析: 根据CE=2,DE=8,得出半径为5,在直角三角形OBE中,由勾股定理得BE,根据垂径定理得出AB的长.
解答: 解:∵CE=2,DE=8,
∴OB=5,
∴OE=3,
∵AB⊥CD,
∴在△OBE中,得BE=4,
∴AB=2BE=8.
故选:D.
点评本题考查了勾股定理以及垂径定理,是基础知识要熟练掌握.
5.如图,CD是⊙O的直径,弦AB⊥CD于E,连接BC、BD,下列结论中不一定正确的是( )
A. AE=BE B.= C.OE=DE D. ∠DBC=90°
考点: 垂径定理;圆周角定理.
专题: 几何图形问题.
分析: 由于CD⊥AB,根据垂径定理有AE=BE,弧AD=弧BD,不能得出OE=DE,直径所对的圆周角等于90°.
解答: 解:∵CD⊥AB,
∴AE=BE,=,
∵CD是⊙O的直径,
∴∠DBC=90°,
不能得出OE=DE.
故选:C.
点评: 本题考查了垂径定理.解题的关键是熟练掌握垂径定理的内容.
6.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是( )
A. 4 B. C. D.
考点:垂径定理;一次函数图象上点的坐标特征;勾股定理.
专题:计算题;压轴题.
分析: PC⊥x轴于C,交AB于D,作PE⊥AB于E,连结PB,由于OC=3,PC=a,易得D点坐标为(3,3),则△OCD为等腰直角三角形,△PED也为等腰直角三角形.由PE⊥AB,根据垂径定理得AE=BE=AB=2,在Rt△PBE中,利用勾股定理可计算出PE=1,则PD=PE=,所以a=3+.
解答: 解:作PC⊥x轴于C,交AB于D,作PE⊥AB于E,连结PB,如图,
∵⊙P的圆心坐标是(3,a),
∴OC=3,PC=a,
把x=3代入y=x得y=3,
∴D点坐标为(3,3),
∴CD=3,
∴△OCD为等腰直角三角形,
∴△PED也为等腰直角三角形,
∵PE⊥AB,
∴AE=BE=AB=×4=2,
在Rt△PBE中,PB=3,
∴PE=,
∴PD=PE=,
∴a=3+.
故选:B.
点评: 本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理和等腰直角三角形的性质.
7.已知⊙O的面积为2π,则其内接正三角形的面积为( )
A. 3 B.3 C. D.
考点: 垂径定理;等边三角形的性质.
专题: 几何图形问题.
分析: 先求出正三角形的外接圆的半径,再求出正三角形的边长,最后求其面积即可.
解答: 解:如图所示,
连接OB、OC,过O作OD⊥BC于D,
∵⊙O的面积为2π
∴⊙O的半径为
∵△ABC为正三角形,
∴∠BOC==120°,∠BOD=∠BOC=60°,OB=,
∴BD=OB?sin∠BOD==,
∴BC=2BD=,
∴OD=OB?cos∠BOD=?cos60°=,
∴△BOC的面积=?BC?OD=××=,
∴△ABC的面积=3S△BOC=3×=.
故选:C.
点评: 本题考查的是三角形的外接圆与外心,根据题意画出图形,利用数形结合求解是解答此题的关键.
8.如图,半径为3的⊙O内有一点A,OA=,点P在⊙O上,当∠OPA最大时,PA的长等于( )
A. B. C.3 D. 2
考点: 垂径定理;圆周角定理.
分析: 当PA⊥OA时,PA取最小值,∠OPA取得最大值,然后在直角三角形OPA中利用勾股定理求PA的值即可.
解答: 解:∵OA、OP是定值,
∴在△OPA中,当∠OPA取最大值时,PA取最小值,
∴PA⊥OA时,PA取最小值;
在直角三角形OPA中,OA=,OP=3,
∴PA==.
故选B.
点评: 本题考查了解直角三角形.解答此题的关键是找出“当PA⊥OA时,PA取最小值”即“PA⊥OA时,∠OPA取最大值”这一隐含条件.
二.填空题(共6小题)
9.如图,已知直线AB与⊙O相交于A、B两点,∠OAB=30°,半径OA=2,那么弦AB= 2 .
考点: 垂径定理;含30度角的直角三角形;勾股定理.
分析: 过O作OC⊥AB于C,根据垂直和垂径定理求出AB=2AC,∠OCA=90°,根据含30度角的直角三角形性质求出OC=1,根据勾股定理求出AC,即可得出答案.
解答: 解:
过O作OC⊥AB于C,
则AB=2AC,∠OCA=90°,
∵OA=2,∠OAB=30°,
∴OC=1,由勾股定理得:AC==,
∴AB=2AC=2,
故答案为:2.
点评: 本题考查了垂径定理,含30度角的直角三角形性质,勾股定理的应用,解此题的关键是正确作出辅助线后求出AC的长和得出AB=2AC,注意:垂直于弦的直径平分这条弦.
10.如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是 32 .
考点: 垂径定理;勾股定理.
分析: 连接OD,先根据垂径定理得出PD=CD=4,再根据勾股定理求出OP的长,根据三角形的面积公式即可得出结论.
解答: 解:连接OD,
∵⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,CD=8,
∴PD=CD=4,
∴OP===3,
∴AP=OA+OP=5+3=8,
∴S△ACD=CD?AP=×8×8=32.
故答案为:32.
点评: 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
11.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .
考点: 垂径定理;轴对称的性质.
分析: A、B两点关于MN对称,因而PA+PC=PB+PC,即当B、C、P在一条直线上时,PA+PC的最小,即BC的值就是PA+PC的最小值
解答: 解:连接OA,OB,OC,作CH垂直于AB于H.
根据垂径定理,得到BE=AB=4,CF=CD=3,
∴OE===3,
OF===4,
∴CH=OE+OF=3+4=7,
BH=BE+EH=BE+CF=4+3=7,
在直角△BCH中根据勾股定理得到BC=7,
则PA+PC的最小值为.
故答案为:
点评: 正确理解BC的长是PA+PC的最小值,是解决本题的关键.
12.如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2cm,∠BCD=22°30′,则⊙O的半径为 2 cm.
考点: 垂径定理;等腰直角三角形;圆周角定理.
专题: 计算题.
分析: 先根据圆周角定理得到∠BOD=2∠BCD=45°,再根据垂径定理得到BE=AB=,且△BOE为等腰直角三角形,然后根据等腰直角三角形的性质求解.
解答: 解:连结OB,如图,
∵∠BCD=22°30′,
∴∠BOD=2∠BCD=45°,
∵AB⊥CD,
∴BE=AE=AB=×2=,△BOE为等腰直角三角形,
∴OB=BE=2(cm).
故答案为:2.
点评: 本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了等腰直角三角形的性质和圆周角定理.
13.如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是 4 .
考点: 垂径定理;圆周角定理.
专题: 计算题.
分析: 过点O作OC⊥AB于C,交⊙O于D、E两点,连结OA、OB、DA、DB、EA、EB,根据圆周角定理得∠AOB=2∠AMB=90°,则△OAB为等腰直角三角形,所以AB=OA=2,由于S四边形MANB=S△MAB+S△NAB,而当M点到AB的距离最大,△MAB的面积最大;当N点到AB的距离最大时,△NAB的面积最大,即M点运动到D点,N点运动到E点,所以四边形MANB面积的最大值=S四边形DAEB=S△DAB+S△EAB=AB?CD+AB?CE=AB(CD+CE)=AB?DE=×2×4=4.
解答: 解:过点O作OC⊥AB于C,交⊙O于D、E两点,连结OA、OB、DA、DB、EA、EB,如图,
∵∠AMB=45°,
∴∠AOB=2∠AMB=90°,
∴△OAB为等腰直角三角形,
∴AB=OA=2,
∵S四边形MANB=S△MAB+S△NAB,
∴当M点到AB的距离最大,△MAB的面积最大;当N点到AB的距离最大时,△NAB的面积最大,
即M点运动到D点,N点运动到E点,
此时四边形MANB面积的最大值=S四边形DAEB=S△DAB+S△EAB=AB?CD+AB?CE=AB(CD+CE)=AB?DE=×2×4=4.
故答案为:4.
点评: 本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理.
14.如图,AB是⊙O的直径,BC是弦,点E是的中点,OE交BC于点D.连接AC,若BC=6,DE=1,则AC的长为 8 .
考点: 垂径定理;勾股定理;三角形中位线定理.
专题: 计算题.
分析: 连接OC,根据圆心角与弧之间的关系可得∠BOE=∠COE,由于OB=OC,根据等腰三角形的性质可得OD⊥BC,BD=CD.在直角三角形BDO中,根据勾股定理可求出OB,进而求出OD长,再根据三角形中位线定理可得AC的长.
解答: 解:连接OC,如图所示.
∵点E是的中点,
∴∠BOE=∠COE.
∵OB=OC,
∴OD⊥BC,BD=DC.
∵BC=6,
∴BD=3.
设⊙O的半径为r,则OB=OE=r.
∵DE=1,
∴OD=r﹣1.
∵OD⊥BC即∠BDO=90°,
∴OB2=BD2+OD2.
∵OB=r,OD=r﹣1,BD=3,
∴r2=32+(r﹣1)2.
解得:r=5.
∴OD=4.
∵AO=BO,BD=CD,
∴OD=AC.
∴AC=8.
点评: 本题考查了在同圆或等圆中等弧所对的圆心角相等、等腰三角形的性质、勾股定理、三角形中位线定理等知识,有一定的综合性.
三.解答题(共7小题)
15.如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形.
考点: 垂径定理;等腰三角形的判定.
专题: 证明题.
分析: 过O作OE⊥AB于E,根据垂径定理求出AE=BE,求出CE=DE,根据线段垂直平分线性质求出OD=OC,即可得出答案.
解答: 证明:
过O作OE⊥AB于E,
则AE=BE,
∵AD=BC,
∴AD﹣DC=BC﹣DC,
∴AC=DE,
∴CE=DE,
∵OE⊥CD,
∴OC=OD,
即△OCD是等腰三角形.
点评: 本题考查了垂径定理,等腰三角形的判定,线段垂直平分线性质的应用,解此题的关键是正确作出辅助线后求出CE=DE.
16.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
考点: 垂径定理;勾股定理.
专题: 几何综合题.
分析: (1)过O作OE⊥AB,根据垂径定理得到AE=BE,CE=DE,从而得到AC=BD;
(2)由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,再根据勾股定理求出CE及AE的长,根据AC=AE﹣CE即可得出结论.
解答: (1)证明:过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE﹣DE=AE﹣CE,即AC=BD;
(2)解:由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,
∴OE=6,
∴CE===2,AE===8,
∴AC=AE﹣CE=8﹣2.
点评: 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
17.如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.
考点: 垂径定理;勾股定理;圆周角定理.
专题: 几何综合题.
分析: (1)先根据CD=16,BE=4,得出OE的长,进而得出OB的长,进而得出结论;
(2)由∠M=∠D,∠DOB=2∠D,结合直角三角形可以求得结果;
解答: 解:(1)∵AB⊥CD,CD=16,
∴CE=DE=8,
设OB=x,
又∵BE=4,
∴x2=(x﹣4)2+82,
解得:x=10,
∴⊙O的直径是20.
(2)∵∠M=∠BOD,∠M=∠D,
∴∠D=∠BOD,
∵AB⊥CD,
∴∠D=30°.
点评: 本题考查了圆的综合题:在同圆或等圆中,相等的弧所对的圆周角相等,直径所对的圆周角为直角;垂直于弦的直径平分弦,并且平分弦所对的弧;
18.如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
考点: 垂径定理;勾股定理.
专题: 几何图形问题.
分析: 过点O作OE⊥AB于点E,连接OB,由垂径定理可知AE=BE=AB,再根据勾股定理求出OE的长,由此可得出结论.
解答: 解:过点O作OE⊥AB于点E,连接OB,
∵AB=8cm,
∴AE=BE=AB=×8=4cm,
∵⊙O的直径为10cm,
∴OB=×10=5cm,
∴OE===3cm,
∵垂线段最短,半径最长,
∴3cm≤OP≤5cm.
点评: 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
19.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
(1)求证:CB∥PD;
(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.
考点: 垂径定理;圆周角定理;弧长的计算.
专题: 几何图形问题.
分析: (1)先根据同弧所对的圆周角相等得出∠PBC=∠D,再由等量代换得出∠C=∠D,然后根据内错角相等两直线平行即可证明CB∥PD;
(2)先由垂径定理及圆周角定理得出∠BOC=2∠PBC=45°,再根据邻补角定义求出∠AOC=135°,然后根据弧长的计算公式即可得出劣弧AC的长度.
解答: 解:(1)∵∠PBC=∠D,∠PBC=∠C,
∴∠C=∠D,
∴CB∥PD;
(2)连结OC,OD.
∵AB是⊙O的直径,弦CD⊥AB于点E,
∴=,
∵∠PBC=∠C=22.5°,
∴∠BOC=∠BOD=2∠C=45°,
∴∠AOC=180°﹣∠BOC=135°,
∴劣弧AC的长为:=.
点评: 本题考查了圆周角定理,平行线的判定,垂径定理,弧长的计算,难度适中.(2)中求出∠AOC=135°是解题的关键.
20.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为E,,
(1)求AB的长;
(2)求⊙O的半径.
考点: 垂径定理;等边三角形的判定与性质.
分析: (1)先根据CD为⊙O的直径,CD⊥AB得出=,故可得出∠C=∠AOD,由对顶角相等得出∠AOD=∠COE,故可得出∠C=∠COE,再根据AO⊥BC可知∠AEC=90°,故∠C=30°,再由直角三角形的性质可得出BF的长,进而得出结论;
(2)在Rt△OCE中根据∠C=30°即可得出OC的长.
解答: 解:(1)∵CD为⊙O的直径,CD⊥AB,
∴=,AF=BF,
∴∠C=∠AOD,
∵∠AOD=∠COE,
∴∠C=∠COE,
∵AO⊥BC,
∴∠AEC=90°,
∴∠C=30°,
∵BC=2,
∴BF=BC=,
∴AB=2BF=2;
(2)∵AO⊥BC,BC=2,
∴CE=BE=BC=,
∵∠C=30°,
∴OC===2,即⊙O的半径是2.
点评: 本题考查的是垂径定理,熟知“平分弦的直径平分这条弦,并且平分弦所对的两条弧”是解答此题的关键.
21.已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:
(1)圆心O到AQ的距离;
(2)线段EF的长.
考点: 垂径定理;含30度角的直角三角形;勾股定理.
分析: (1)过点O作OH⊥EF,垂足为点H,求出AO,根据含30度角的直角三角形性质求出即可;
(2)连接OE,根据勾股定理求出EH,根据垂径定理得出即可.
解答: 解:(1)过点O作OH⊥EF,垂足为点H,
∵OH⊥EF,
∴∠AHO=90°,
在Rt△AOH中,∵∠AHO=90°,∠PAQ=30°,
∴OH=AO,
∵BC=10cm,
∴BO=5cm.
∵AO=AB+BO,AB=3cm,
∴AO=3+5=8cm,
∴OH=4cm,即圆心O到AQ的距离为4cm.
(2)连接OE,
在Rt△EOH中,
∵∠EHO=90°,∴EH2+HO2=EO2,
∵EO=5cm,OH=4cm,
∴EH===3cm,
∵OH过圆心O,OH⊥EF,
∴EF=2EH=6cm.
点评: 本题考查了含30度角的直角三角形性质,勾股定理,垂径定理的应用,题目是一道比较典型的题目,难度适中.
