北师大版七年级数学下册 3.2用关系式表示变量之间的关系课件(共16张ppt)
文档属性
| 名称 | 北师大版七年级数学下册 3.2用关系式表示变量之间的关系课件(共16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 631.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-11 10:46:01 | ||
图片预览






文档简介
(共16张PPT)
北师大版七年级数学下册第三章变量之间的关系
3.2用关系式表示的变量之间的关系
一、学习目标
1.能根据具体情况,用关系式表示某些变量之间的关系.
2.能根据关系式求值,体会自变量和因变量的数值对应关系.
3、根据关系式找自变量与因变量之间的对应关系。
二、温故知新
1、填空
(1)如果△ABC的底边长为a,高为h,那么面积S△ABC=_____________.
(2)如果梯形的上底、下底长分别为a、b,高为h,那么面积S梯形=___________.
(3)圆的半径为r,则圆的面积S= 。
(4)圆柱的底面半径为r,高为h,体积V圆柱=__________
(5)圆锥底面的半径为r,高为h,体积V圆锥=____________.
(6)如果正方形的边长为a,则正方形的周长C=________;面积S=________
ah
(a+b)h
h
h
4a
n 1 2 3 4 5 6 7
m 4 5 6 7 8 9 10
2.观察下表并回答问题:
(1)表格反映的是哪两个变量的关系?谁是自变量?谁是因变量?
(2)你能否将m用n的代数式表示出来?
解:(1)表格反映的变量m,n之间的关系,其中n是自变量,m是因变量
(2)m=n+3
三、自主探究:阅读课本p66-67
三角形是日常生活中很常见的图形,决定一个三角形面积的因素
有 、 。
如图所示,△ABC底边BC上的高是6cm.当三角形的顶点C沿
底边所在直线向点B运动时,三角形的面积发生了怎样的变化?
在这个变化过程中,△ABC中的哪些因素在改变?
(1)在这个变化过程中,自变量是________,
因变量是__________.
(2)如果三角形的底边长为x(cm),
那么三角形的面积y(cm 2)可以表示为______
(3)当底边长从12 cm变化到3 cm时,三角形的
面积从_____cm 2变化到_____ cm 2 .
(4)当x分别等于1,2,3,4时,对应的y的值分别为__________。
底边 高
当三角形的顶点C沿底边所在直线向点B运动时,三角形面积逐渐变小;在这个变化过程中,△ABC中的底边长和面积在改变
底边长
面积
y=3x
36
9
3,6,9,12
归纳:
1、y=3x表示了 和 之间的关系,它是变量y随x变化的关系式。
2、通过表格可表示两个变量之间的关系,本节中利用_______也
可表示两个变量之间的关系.
3、确定关系式的步骤:先找出题目中关于________与________的
相等关系,再用_____________ 的代数式表示________
①写关系式时将表示 的字母单独写在等号的左边。
②利用关系式可以根据任何一个 的值求出相应的 的值。
x y
关系式
自变量
因变量
含自变量
因变量
因变量
自变量
因变量
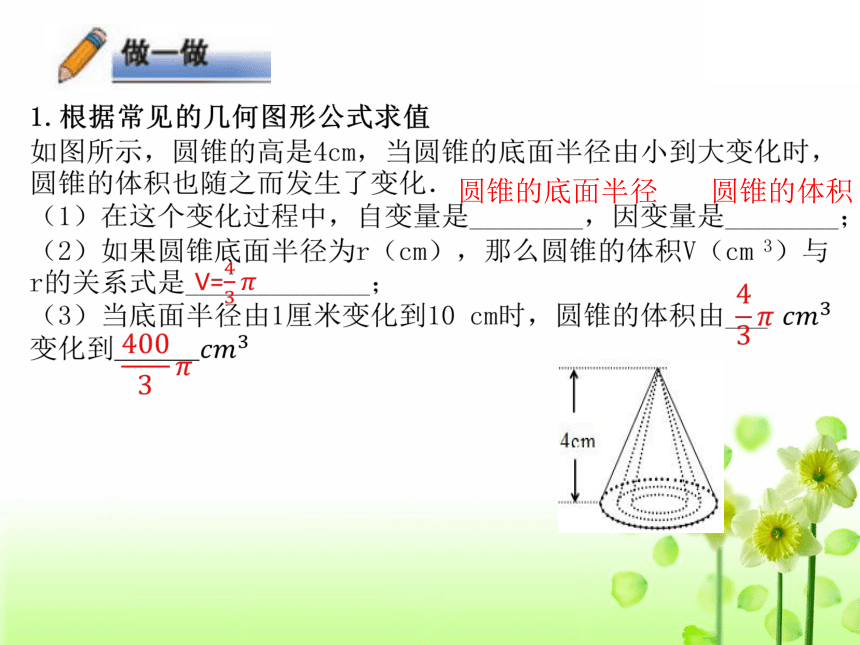
1.根据常见的几何图形公式求值
如图所示,圆锥的高是4cm,当圆锥的底面半径由小到大变化时,
圆锥的体积也随之而发生了变化.
(1)在这个变化过程中,自变量是________,因变量是________;
(2)如果圆锥底面半径为r(cm),那么圆锥的体积V(cm 3)与
r的关系式是_____________;
(3)当底面半径由1厘米变化到10 cm时,圆锥的体积由___
变化到
圆锥的底面半径
圆锥的体积
V=
2.关系式在日常生活中的应用
你知道什么是“低碳生活”吗?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳、特别是二氧化碳的排放量的一种方式。
(1)家居用电的二氧化碳排放量可以用关系式表示为____________,其中的字母表示_____________。
(2)在上述关系式中,耗电量每增加1 KW·h,二氧化碳
排放量增加_________。
当耗电量从1 KW·h增加到100 KW·h时,二氧化碳排放量
从___________增加到___________。
y=0.785x
x表示耗电量,y表示
家居二氧化碳排放量
0.785kg
0.785kg
78.5kg
(3)小明家本月用电大约110 KW·h、天然气20m3、自来水5t、
油耗75L,请你计算一下小明家这几项的二氧化碳排放量。
解:家居用电的二氧化碳排放量是110×0.785=86.35kg
家用天然气的二氧化碳排放量是20×0.19=3.8kg
家用自来水的二氧化碳排放量是5×0.91=4.55kg
开私家车的二氧化碳排放量是75×2.7=202.5kg
四、随堂练习 :
在地球某地,温度T(°C)与高度d之间的关系可以近似地用T=10- 来表示,根据这个关系式,当d的值分别是0,200,400,600,800,1000时,计算相应的T值,并用表格表示所得结果。
?
d 0 200 400 600 800 1000
T 10 6
用关系式表示变量间的关系要明确“三点”:
(1)关系式是用含自变量的代数式表示因变量的等式.
(2)利用关系式表示变量之间的关系,最大的优点在于能比较
方便地求出自变量为取值范围内的任意一个值时,相对应
的因变量的值.利用表格表示变量之间的关系时,对于表
格中没有给出的对应值,在需要时往往只能估计,很难达
到足够的精确度,使用关系式则没有这样的缺点.
(3)利用关系式求因变量的值,实际上就是求代数式的值.
今天我们学了什么
六.当堂检测:
1.若干张长为20cm、宽为10cm的长方形白纸,按下图所示的方法
粘合起来,粘合部分的宽为2cm.
(1)求4张白纸粘合后的总长度;
(2)设x张白纸粘合后的总长度为ycm,写出y与x之间的关系式;
(3)并求当x=20时,y的值
解:(1)4张白纸粘合后的总长度是20×4-3×2=74(厘米);
(2)y=20x-2(x-1)=18x+2
(3)当x=20时,y=362。
2、某种长途电话收费方式为按时收费,前3分钟收费1.8元,以后每加一分钟收费1元,求:
(1)当时间t≥3分钟时的电话费y (元)与t (分) 之间的关系.
(2)计算当时间分别为5分、10分、30分、50分的电话费
解:(1)当时间t≥3分钟时的电话费y(元)与t(分)之间的关系式为y=(t-3)+1.8=t-1.2;
所以y=t-1.2
(2)当t=5时,y=3.8; 当t=10时,y=8.8
当t=30时,y=28.8; 当t=50时,y=48.8
课后作业:
1.地表以下岩层的温度y(°c)随着所处深度x(km)的变化而变化,在每个地点y与x之间的关系可以近似地用关系式y=35x+20来表示,当x的值分别是2,3,5,7,10,13时,计算相应的y值。
解:当x=2时,y=35×1+20=55
当x=3时,y=35×3+20=125
当x=5时,y=35×5+20=195
当x=7时,y=35×7+20=265
当x=10时,y=35×10+20=370
当x=13时,y=35×13+20=475
2.如图,圆锥的底面半径是2cm,当圆锥的高由小到大变化时,
圆锥的体积页随之发生了变化.
在这个变化过程中,自变量、因变量各是什么?
(2)如果圆锥的高为h(cm),那么圆锥的体积V()与h的关系式为________.
(3)当高由1cm变化到10cm时,圆锥的体积由____ 变化到______ .
解:在这个变化过程中,自变量是圆锥的高、因变量是圆锥的体积
V=
3.如图所示,梯形上底的长是x,下底的长是15,高是8.
(1)梯形的面积y与上底x之间的关系式是什么?
(2)用表格表示当x从4变到14时(每次增加1),y的相应值;
(3)当x每增加1时,y如何变化?说说你的理由;
(4)当x=0时,y等于什么?此时图形是什么?
1.关系式:y=4x+60;
2.
3.当x每增加1时,y增加4,理由:x的系数为4。
4.当x=0时,y=60。此时的图形是一个三角形
x 4 5 6 7 8 9 10 11 12 13 14
y 76 80 84 88 92 96 100 104 108 112 116
北师大版七年级数学下册第三章变量之间的关系
3.2用关系式表示的变量之间的关系
一、学习目标
1.能根据具体情况,用关系式表示某些变量之间的关系.
2.能根据关系式求值,体会自变量和因变量的数值对应关系.
3、根据关系式找自变量与因变量之间的对应关系。
二、温故知新
1、填空
(1)如果△ABC的底边长为a,高为h,那么面积S△ABC=_____________.
(2)如果梯形的上底、下底长分别为a、b,高为h,那么面积S梯形=___________.
(3)圆的半径为r,则圆的面积S= 。
(4)圆柱的底面半径为r,高为h,体积V圆柱=__________
(5)圆锥底面的半径为r,高为h,体积V圆锥=____________.
(6)如果正方形的边长为a,则正方形的周长C=________;面积S=________
ah
(a+b)h
h
h
4a
n 1 2 3 4 5 6 7
m 4 5 6 7 8 9 10
2.观察下表并回答问题:
(1)表格反映的是哪两个变量的关系?谁是自变量?谁是因变量?
(2)你能否将m用n的代数式表示出来?
解:(1)表格反映的变量m,n之间的关系,其中n是自变量,m是因变量
(2)m=n+3
三、自主探究:阅读课本p66-67
三角形是日常生活中很常见的图形,决定一个三角形面积的因素
有 、 。
如图所示,△ABC底边BC上的高是6cm.当三角形的顶点C沿
底边所在直线向点B运动时,三角形的面积发生了怎样的变化?
在这个变化过程中,△ABC中的哪些因素在改变?
(1)在这个变化过程中,自变量是________,
因变量是__________.
(2)如果三角形的底边长为x(cm),
那么三角形的面积y(cm 2)可以表示为______
(3)当底边长从12 cm变化到3 cm时,三角形的
面积从_____cm 2变化到_____ cm 2 .
(4)当x分别等于1,2,3,4时,对应的y的值分别为__________。
底边 高
当三角形的顶点C沿底边所在直线向点B运动时,三角形面积逐渐变小;在这个变化过程中,△ABC中的底边长和面积在改变
底边长
面积
y=3x
36
9
3,6,9,12
归纳:
1、y=3x表示了 和 之间的关系,它是变量y随x变化的关系式。
2、通过表格可表示两个变量之间的关系,本节中利用_______也
可表示两个变量之间的关系.
3、确定关系式的步骤:先找出题目中关于________与________的
相等关系,再用_____________ 的代数式表示________
①写关系式时将表示 的字母单独写在等号的左边。
②利用关系式可以根据任何一个 的值求出相应的 的值。
x y
关系式
自变量
因变量
含自变量
因变量
因变量
自变量
因变量
1.根据常见的几何图形公式求值
如图所示,圆锥的高是4cm,当圆锥的底面半径由小到大变化时,
圆锥的体积也随之而发生了变化.
(1)在这个变化过程中,自变量是________,因变量是________;
(2)如果圆锥底面半径为r(cm),那么圆锥的体积V(cm 3)与
r的关系式是_____________;
(3)当底面半径由1厘米变化到10 cm时,圆锥的体积由___
变化到
圆锥的底面半径
圆锥的体积
V=
2.关系式在日常生活中的应用
你知道什么是“低碳生活”吗?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳、特别是二氧化碳的排放量的一种方式。
(1)家居用电的二氧化碳排放量可以用关系式表示为____________,其中的字母表示_____________。
(2)在上述关系式中,耗电量每增加1 KW·h,二氧化碳
排放量增加_________。
当耗电量从1 KW·h增加到100 KW·h时,二氧化碳排放量
从___________增加到___________。
y=0.785x
x表示耗电量,y表示
家居二氧化碳排放量
0.785kg
0.785kg
78.5kg
(3)小明家本月用电大约110 KW·h、天然气20m3、自来水5t、
油耗75L,请你计算一下小明家这几项的二氧化碳排放量。
解:家居用电的二氧化碳排放量是110×0.785=86.35kg
家用天然气的二氧化碳排放量是20×0.19=3.8kg
家用自来水的二氧化碳排放量是5×0.91=4.55kg
开私家车的二氧化碳排放量是75×2.7=202.5kg
四、随堂练习 :
在地球某地,温度T(°C)与高度d之间的关系可以近似地用T=10- 来表示,根据这个关系式,当d的值分别是0,200,400,600,800,1000时,计算相应的T值,并用表格表示所得结果。
?
d 0 200 400 600 800 1000
T 10 6
用关系式表示变量间的关系要明确“三点”:
(1)关系式是用含自变量的代数式表示因变量的等式.
(2)利用关系式表示变量之间的关系,最大的优点在于能比较
方便地求出自变量为取值范围内的任意一个值时,相对应
的因变量的值.利用表格表示变量之间的关系时,对于表
格中没有给出的对应值,在需要时往往只能估计,很难达
到足够的精确度,使用关系式则没有这样的缺点.
(3)利用关系式求因变量的值,实际上就是求代数式的值.
今天我们学了什么
六.当堂检测:
1.若干张长为20cm、宽为10cm的长方形白纸,按下图所示的方法
粘合起来,粘合部分的宽为2cm.
(1)求4张白纸粘合后的总长度;
(2)设x张白纸粘合后的总长度为ycm,写出y与x之间的关系式;
(3)并求当x=20时,y的值
解:(1)4张白纸粘合后的总长度是20×4-3×2=74(厘米);
(2)y=20x-2(x-1)=18x+2
(3)当x=20时,y=362。
2、某种长途电话收费方式为按时收费,前3分钟收费1.8元,以后每加一分钟收费1元,求:
(1)当时间t≥3分钟时的电话费y (元)与t (分) 之间的关系.
(2)计算当时间分别为5分、10分、30分、50分的电话费
解:(1)当时间t≥3分钟时的电话费y(元)与t(分)之间的关系式为y=(t-3)+1.8=t-1.2;
所以y=t-1.2
(2)当t=5时,y=3.8; 当t=10时,y=8.8
当t=30时,y=28.8; 当t=50时,y=48.8
课后作业:
1.地表以下岩层的温度y(°c)随着所处深度x(km)的变化而变化,在每个地点y与x之间的关系可以近似地用关系式y=35x+20来表示,当x的值分别是2,3,5,7,10,13时,计算相应的y值。
解:当x=2时,y=35×1+20=55
当x=3时,y=35×3+20=125
当x=5时,y=35×5+20=195
当x=7时,y=35×7+20=265
当x=10时,y=35×10+20=370
当x=13时,y=35×13+20=475
2.如图,圆锥的底面半径是2cm,当圆锥的高由小到大变化时,
圆锥的体积页随之发生了变化.
在这个变化过程中,自变量、因变量各是什么?
(2)如果圆锥的高为h(cm),那么圆锥的体积V()与h的关系式为________.
(3)当高由1cm变化到10cm时,圆锥的体积由____ 变化到______ .
解:在这个变化过程中,自变量是圆锥的高、因变量是圆锥的体积
V=
3.如图所示,梯形上底的长是x,下底的长是15,高是8.
(1)梯形的面积y与上底x之间的关系式是什么?
(2)用表格表示当x从4变到14时(每次增加1),y的相应值;
(3)当x每增加1时,y如何变化?说说你的理由;
(4)当x=0时,y等于什么?此时图形是什么?
1.关系式:y=4x+60;
2.
3.当x每增加1时,y增加4,理由:x的系数为4。
4.当x=0时,y=60。此时的图形是一个三角形
x 4 5 6 7 8 9 10 11 12 13 14
y 76 80 84 88 92 96 100 104 108 112 116
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
