三 圆的切线的性质及判定定理(共23张PPT)
文档属性
| 名称 | 三 圆的切线的性质及判定定理(共23张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-11 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
相交:直线与圆有两个公共点;
相切:直线与圆只有一个公共点;
相离:直线与圆没有公共点.
直线和圆的位置关系?
如图,直线L与圆O相切,此时有什么性质呢?
直线L与OA垂直?
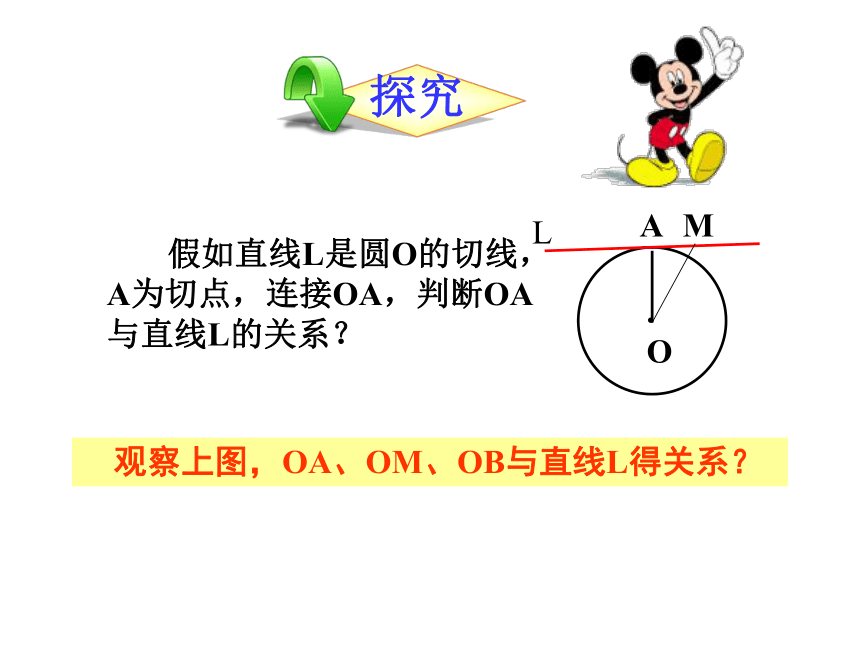
观察上图,OA、OM、OB与直线L得关系?
假如直线L是圆O的切线,A为切点,连接OA,判断OA与直线L的关系?
已知直线L与圆O相切,A为切点,
求证:OA⊥L.
证明:
假设L与OA不垂直,则过O点作OM⊥L,垂足为M,
根据“垂线段最短”的性质,得:
OA>OM.
∴圆心到直线L的距离小于圆的半径,于是得L与圆O相交,
这与L是圆O的切线相矛盾,
因此:L与OA一定垂直.
知识要点
切线性质定理:
圆的切线垂直于经过切点的半径 .
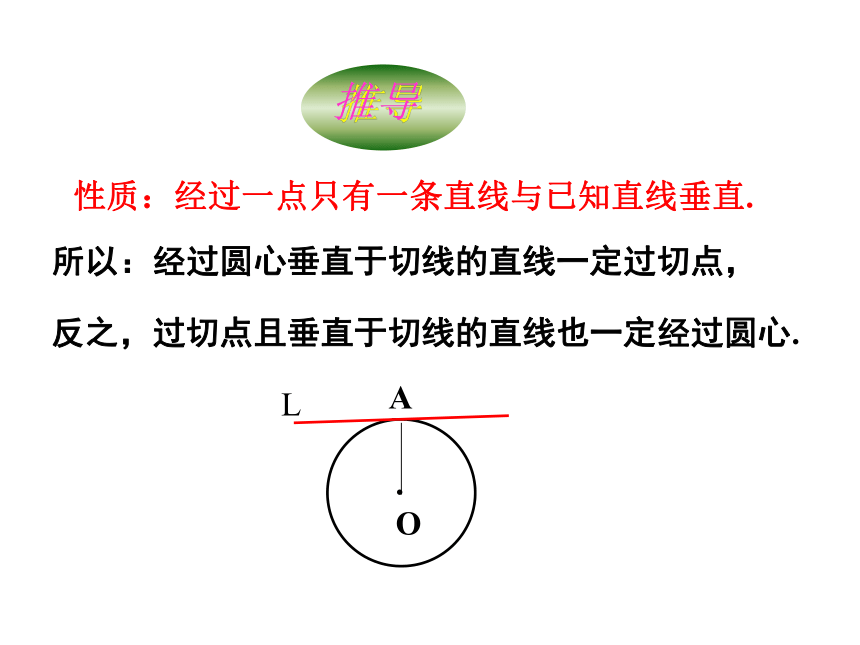
性质:经过一点只有一条直线与已知直线垂直.
所以:经过圆心垂直于切线的直线一定过切点,
反之,过切点且垂直于切线的直线也一定经过圆心.
知识要点
推论1:
经过圆心且垂直于切线的直线必经过切点 .
知识要点
推论2:
经过切点且垂直于切线的直线必经过圆心.
如图, 直线l是圆O的切线, 切点为A, ∠OBA=40°,
求∠AOB.
·
O
A
B
40°
解: 由于线段OA是过切点的半径,
因此 OA ⊥l,从而∠OAB=90°,
于是∠AOB=90-40°
= 50°
圆的切线垂直于经过切点的半径.
讨论:如果经过圆半径的外端并且垂直于这条半径做一条直线,那么是否可以推出这条直线就是圆的切线呢?
圆的切线的判定定理?
已知点A是圆O与直线L的公共点且L⊥OA
求证:L是经过点A的圆的切线.
分析:
在直线L上任取异于点A的点B,有OB>OA,
因为△OBA是直角三角形,而OB是直角三角形的斜边;
所以:点B在圆外,由点B的任意性,
得圆与直线只有一个公共点,所以L是圆的切线.
知识要点
圆的切线判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
如图, AB是圆O的直径,圆O过BC的中点D,DE⊥AC,
求证:DE是圆O的切线.
连接OD,∵BD=CD,OA=OB,
∴OD是△ABC的中位线
∴OD//AC.
又∵∠DEC=900, ∴ ∠ODE=900.
又∵D在圆周上,
∴DE是圆O的切线.
证明:
圆的切线垂直于经过切点的半径.
1、圆的切线的性质定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
2、圆的切线的判定定理
2、圆的切线性质定理的推论
推论1 经过圆心且垂直于切线的直线必经过切点.
推论2 经过切点且垂直于切线的直线必经过圆心.
1、如图,AB与⊙O切于C点,OA=OB.若⊙O的直径为6cm,AB=8cm,则OA的长 ( )
A.4 B.5 C. 6 D.7
B
连接OC,所以OC⊥AB,
又∵OA=OB, ∴C是AB的中点.
在直角三角形OAC中,OC=3,AC=4, ∴OA=5.
解析
因此l1 ∥ l2. (垂直同一条直线的两条直线平行)
2.已知:如图,AB是圆O的直径, l1 分别是经过点A,B的切线.
求证: l1∥l2.
∵OA是圆O的半径,l是过点A的切线,
∴l1 ⊥OA. (切线判定定理 )
同理l2 ⊥ OB.
从而l1 ⊥ AB, 且l2 ⊥ AB.
证明:
3、如图,这是手表的圆形表盘,两个圆的圆心都是O,大圆的弦AB所在直线是小圆的切线,切点为C,
证明:
求证:C是线段AB的中点.
∴C为AB的中点
两个同心圆.连接OA,OB
∴△OAB为等腰三角形
OA=OB
C为切点,OC⊥AB
即OC为△ABO的高,
∴OC为△ABO的中线
直线l就是所求作的切线,如图
·
O
·A
l
4.求作:过圆O上一点A画圆O的切线.
过圆O上一点A的切线l与半径OA有什么关系?
据切线的性质定理, l ⊥OA,
由此受到启发,过点A作一条直线l与OA垂直,
据切线的判定定理,
L 就是圆O的切线.
作法:
⑴连结OA;
⑵过点A作直线l与OA垂直.
分析:
习题2.3(第32页)
相交:直线与圆有两个公共点;
相切:直线与圆只有一个公共点;
相离:直线与圆没有公共点.
直线和圆的位置关系?
如图,直线L与圆O相切,此时有什么性质呢?
直线L与OA垂直?
观察上图,OA、OM、OB与直线L得关系?
假如直线L是圆O的切线,A为切点,连接OA,判断OA与直线L的关系?
已知直线L与圆O相切,A为切点,
求证:OA⊥L.
证明:
假设L与OA不垂直,则过O点作OM⊥L,垂足为M,
根据“垂线段最短”的性质,得:
OA>OM.
∴圆心到直线L的距离小于圆的半径,于是得L与圆O相交,
这与L是圆O的切线相矛盾,
因此:L与OA一定垂直.
知识要点
切线性质定理:
圆的切线垂直于经过切点的半径 .
性质:经过一点只有一条直线与已知直线垂直.
所以:经过圆心垂直于切线的直线一定过切点,
反之,过切点且垂直于切线的直线也一定经过圆心.
知识要点
推论1:
经过圆心且垂直于切线的直线必经过切点 .
知识要点
推论2:
经过切点且垂直于切线的直线必经过圆心.
如图, 直线l是圆O的切线, 切点为A, ∠OBA=40°,
求∠AOB.
·
O
A
B
40°
解: 由于线段OA是过切点的半径,
因此 OA ⊥l,从而∠OAB=90°,
于是∠AOB=90-40°
= 50°
圆的切线垂直于经过切点的半径.
讨论:如果经过圆半径的外端并且垂直于这条半径做一条直线,那么是否可以推出这条直线就是圆的切线呢?
圆的切线的判定定理?
已知点A是圆O与直线L的公共点且L⊥OA
求证:L是经过点A的圆的切线.
分析:
在直线L上任取异于点A的点B,有OB>OA,
因为△OBA是直角三角形,而OB是直角三角形的斜边;
所以:点B在圆外,由点B的任意性,
得圆与直线只有一个公共点,所以L是圆的切线.
知识要点
圆的切线判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
如图, AB是圆O的直径,圆O过BC的中点D,DE⊥AC,
求证:DE是圆O的切线.
连接OD,∵BD=CD,OA=OB,
∴OD是△ABC的中位线
∴OD//AC.
又∵∠DEC=900, ∴ ∠ODE=900.
又∵D在圆周上,
∴DE是圆O的切线.
证明:
圆的切线垂直于经过切点的半径.
1、圆的切线的性质定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
2、圆的切线的判定定理
2、圆的切线性质定理的推论
推论1 经过圆心且垂直于切线的直线必经过切点.
推论2 经过切点且垂直于切线的直线必经过圆心.
1、如图,AB与⊙O切于C点,OA=OB.若⊙O的直径为6cm,AB=8cm,则OA的长 ( )
A.4 B.5 C. 6 D.7
B
连接OC,所以OC⊥AB,
又∵OA=OB, ∴C是AB的中点.
在直角三角形OAC中,OC=3,AC=4, ∴OA=5.
解析
因此l1 ∥ l2. (垂直同一条直线的两条直线平行)
2.已知:如图,AB是圆O的直径, l1 分别是经过点A,B的切线.
求证: l1∥l2.
∵OA是圆O的半径,l是过点A的切线,
∴l1 ⊥OA. (切线判定定理 )
同理l2 ⊥ OB.
从而l1 ⊥ AB, 且l2 ⊥ AB.
证明:
3、如图,这是手表的圆形表盘,两个圆的圆心都是O,大圆的弦AB所在直线是小圆的切线,切点为C,
证明:
求证:C是线段AB的中点.
∴C为AB的中点
两个同心圆.连接OA,OB
∴△OAB为等腰三角形
OA=OB
C为切点,OC⊥AB
即OC为△ABO的高,
∴OC为△ABO的中线
直线l就是所求作的切线,如图
·
O
·A
l
4.求作:过圆O上一点A画圆O的切线.
过圆O上一点A的切线l与半径OA有什么关系?
据切线的性质定理, l ⊥OA,
由此受到启发,过点A作一条直线l与OA垂直,
据切线的判定定理,
L 就是圆O的切线.
作法:
⑴连结OA;
⑵过点A作直线l与OA垂直.
分析:
习题2.3(第32页)
