一 平行线等分线段定理(共30张PPT)
文档属性
| 名称 | 一 平行线等分线段定理(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-11 21:32:09 | ||
图片预览






文档简介
(共30张PPT)
回顾旧知
平行线的性质和判定定理
还记得吗?
性质:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补.
同位角相等,两直线平行;
判定:
内错角相等,两直线平行;
同旁内角互补,两直线平行.
一组平行线被两线所截,会有什么性质呢?
1.掌握平行线等分线段定理以及2个推论.
2.能运用定理和推论解决相关几何问题.
知识与能力
1.通过初中学习平行线的性质和判定定理,进一步学习一组平行线等分线段定理以及两个推论.
2.培养化归思想,从特殊到一般,再到特殊.
过程与方法
1.通过平行线等分线段定理证明,体会数学证明的必要性.
2.通过课堂学习培养敢于结合以前所学知识,推导出新的知识或性质,有利于深刻理解.
情感态度与价值观
平行线等分线段定理及两个推论.
重点
灵活应用定理和推论解决相关几何问题.
难点
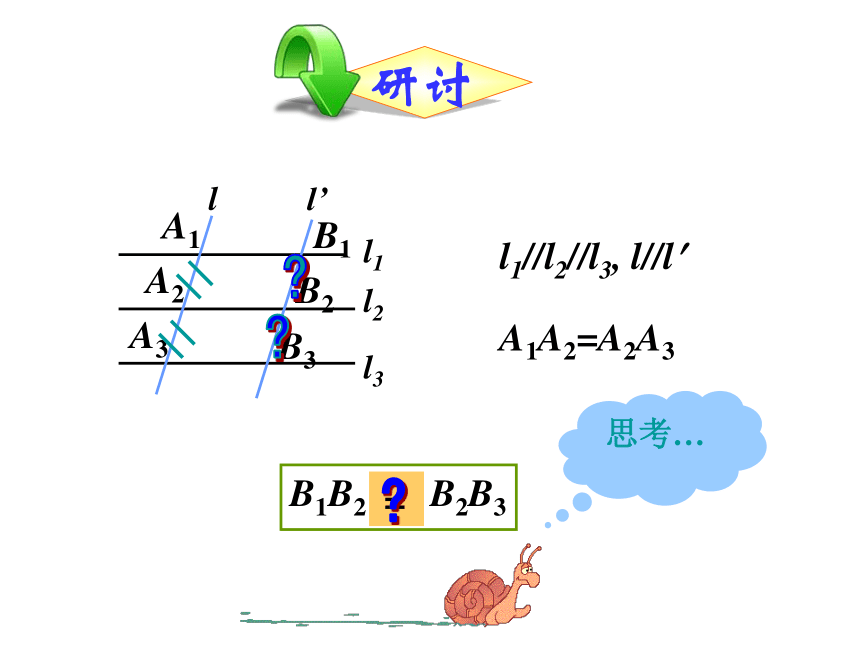
l1//l2//l3, l//l?
A1A2=A2A3
B1B2 B2B3
=
思考…
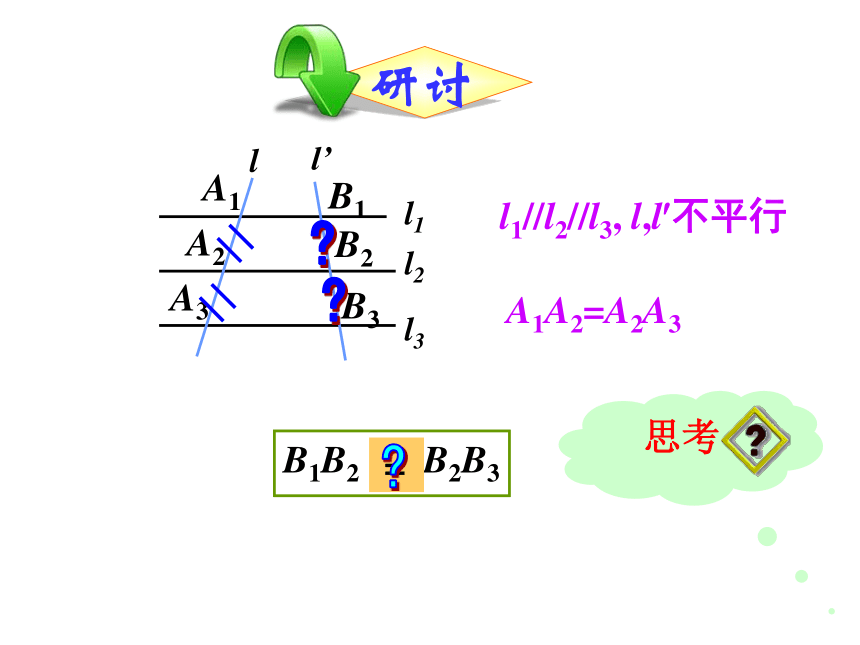
l1//l2//l3, l,l?不平行
A1A2=A2A3
B1B2 B2B3
=
思考
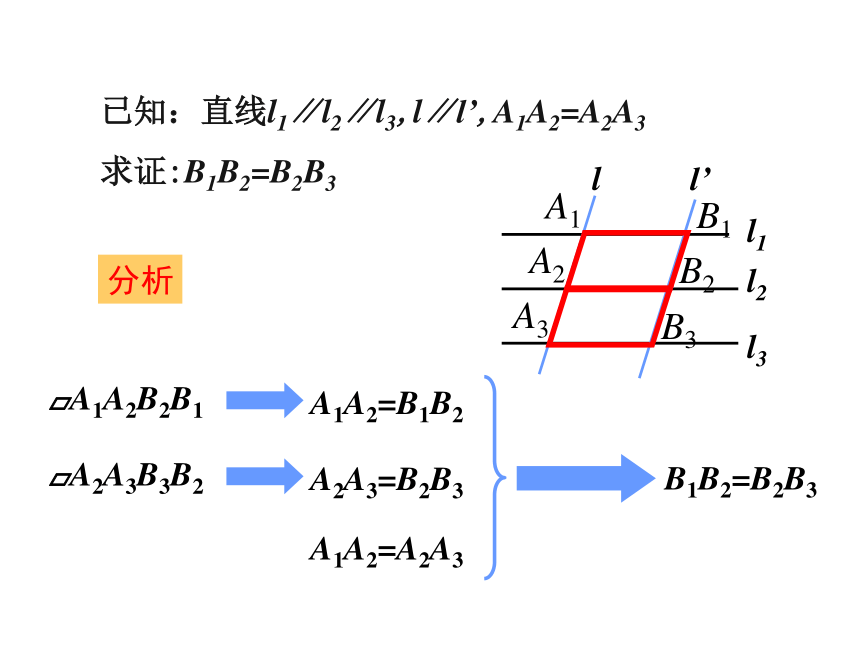
已知:直线l1∥l2∥l3,l∥l’,A1A2=A2A3
求证:B1B2=B2B3
分析
A1A2=A2A3
C2
C3
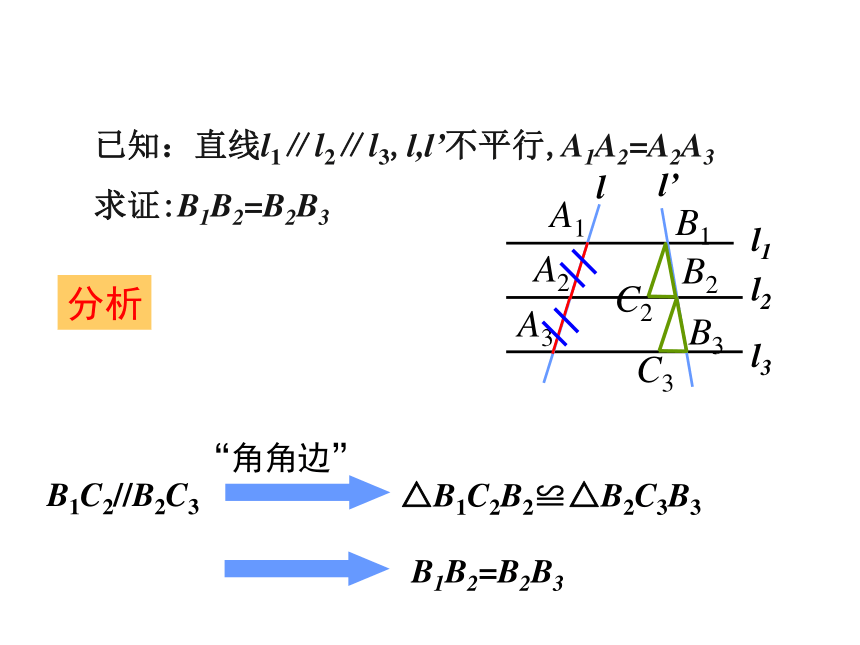
已知:直线l1∥l2∥l3,l,l’不平行,A1A2=A2A3
求证:B1B2=B2B3
分析
B1C2//B2C3
平行线等分线段定理
如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.
已知:ΔABC,D是AB的中点,DE//BC
求证: AE=EC
证明:
因为AD=BD,DE//BC
根据平行线等分线段定理,得:
AE=EC.
能推出什么结论?
知识要点
平行线等分线段定理
推论1:经过三角形一边的中点与另一边平行的直线必平分第三边.
已知:梯形ABCD,E是AB的中点,
求证:CF=DF.
证明:
因为AE=BE,AC//BD
根据平行线等分线段定理,得:
CF=DF.
同样能推出什么结论?
知识要点
平行线等分线段定理
推论2:经过梯形一腰的中点,且与底边平行的直线必平分另一腰.
定理
推论
如图△ABC中点D、E三等分AB,DF∥EG∥BC,DF、EG分别交AC于点F、G,则AF,FG,GC的关系.
根据平行线等分线段定理,得:
AF=FG=GC.
1、平行线等分线段定理
如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.
很重要!
2、平行线等分线段定理的推论
推论1:经过三角形一边的中点与另一边平行的直线必平分第三边.
推论2:经过梯形一腰的中点,且与底边平行的直线必平分另一腰.
理解!
3、平行线等分线段定理和推论的应用
(1)把线段n等分.
(2)证明在同一直线上的线段相等.
1.判断题
(1)如图四边形ABCD中,点M、N分别在AB、CD上若AM=BM、DN=CN 则AD∥MN∥BC ( )
(2)一组平行线,任意相邻的两平行线间的距离都相等,则这组平行线能等分线段 ( )
(3)如图l1∥l2∥l3且AB=BC,那么AB=BC=DE=EF ( )
2.已知:线段AB, 求作:线段AB的五等分点.
A
B
P
问题1: 求作一点P把线段AB分成2:3?
问题2: 如果把△ABC的面积分成2:3?
3.已知:如图,梯形ABCD中,AD∥BC,∠ABC=90°M是CD的中点.
求证:AM=BM
A
B
C
D
M
证明:过M点作ME∥AD交AB于点E
又∵在梯形ABCD中,MD=MC
∴AE=EB
易证ME是AB的垂直平分线,∴AM=BM
4.利用平行线等分线段定理,证明三角形中位线定理.
D、E 分别是△ABC中AB边和AC边的中点.
求证:DE//BC且
作DE?//BC
作DF//AC
=DE
∴DE//BC且DE=1/2BC.
5.如图:有块直角三角形菜地,分配给张,王,李三家农民耕种,已知张,王,李三家人口分别为2人,4人,6人,菜地分配方法按人口比例,并要求每户土地均有一部分紧靠水渠AB,P处是三家合用的肥料仓库,所以点P必须是三家地的交界地
要求:用尺规在图中作出
各家菜地的分界线.
习题1.1(第5页)
1.设AB的长为6厘米.
(1) 过点A作射线AC;
(2) 在射线AC上以适当的长度顺序截取AD=DE=EF=FG=GH=HK=KM;
(3) 过D、E、F、G、H、K作BM的平行线,分别交AB于点D’、E’、F’、G’、H’、K’.则D’、E’、F’、G’、H’、K’即为线段AB的七等分点.
2.猜想:BE=EF=FD.
证明如图,因为M是AB的中点,N是DC的中点,四边形AB-CD是平行四边形,
所以AM//CN,且AM=CN.
所以四边形ANCN是平行四边形.
所以MC//AN.
即:ME平分BF,即BE=EF.
同理可证:FD=EF.
所以:BE=EF=FD.
3. 如图,因为E,F分别是梯形ABCD中AB、DC边上的中点,所以EF//AD,EF//BC.
所以G、H分别是梯形对角线BD、AC的中点.
所以,EG=1/2AD,FH=1/2AD,EH=1/2BC,FG=1/2BC.
又因为GH=EH-EG,GH=FG-FH,
所以,2GH=EH+FG-(EG+FH)
=1/2BC+1/2BC-(1/2AD+1/2AD)
=BC-AD.
所以,GH=1/2(BC-AD).
回顾旧知
平行线的性质和判定定理
还记得吗?
性质:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补.
同位角相等,两直线平行;
判定:
内错角相等,两直线平行;
同旁内角互补,两直线平行.
一组平行线被两线所截,会有什么性质呢?
1.掌握平行线等分线段定理以及2个推论.
2.能运用定理和推论解决相关几何问题.
知识与能力
1.通过初中学习平行线的性质和判定定理,进一步学习一组平行线等分线段定理以及两个推论.
2.培养化归思想,从特殊到一般,再到特殊.
过程与方法
1.通过平行线等分线段定理证明,体会数学证明的必要性.
2.通过课堂学习培养敢于结合以前所学知识,推导出新的知识或性质,有利于深刻理解.
情感态度与价值观
平行线等分线段定理及两个推论.
重点
灵活应用定理和推论解决相关几何问题.
难点
l1//l2//l3, l//l?
A1A2=A2A3
B1B2 B2B3
=
思考…
l1//l2//l3, l,l?不平行
A1A2=A2A3
B1B2 B2B3
=
思考
已知:直线l1∥l2∥l3,l∥l’,A1A2=A2A3
求证:B1B2=B2B3
分析
A1A2=A2A3
C2
C3
已知:直线l1∥l2∥l3,l,l’不平行,A1A2=A2A3
求证:B1B2=B2B3
分析
B1C2//B2C3
平行线等分线段定理
如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.
已知:ΔABC,D是AB的中点,DE//BC
求证: AE=EC
证明:
因为AD=BD,DE//BC
根据平行线等分线段定理,得:
AE=EC.
能推出什么结论?
知识要点
平行线等分线段定理
推论1:经过三角形一边的中点与另一边平行的直线必平分第三边.
已知:梯形ABCD,E是AB的中点,
求证:CF=DF.
证明:
因为AE=BE,AC//BD
根据平行线等分线段定理,得:
CF=DF.
同样能推出什么结论?
知识要点
平行线等分线段定理
推论2:经过梯形一腰的中点,且与底边平行的直线必平分另一腰.
定理
推论
如图△ABC中点D、E三等分AB,DF∥EG∥BC,DF、EG分别交AC于点F、G,则AF,FG,GC的关系.
根据平行线等分线段定理,得:
AF=FG=GC.
1、平行线等分线段定理
如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.
很重要!
2、平行线等分线段定理的推论
推论1:经过三角形一边的中点与另一边平行的直线必平分第三边.
推论2:经过梯形一腰的中点,且与底边平行的直线必平分另一腰.
理解!
3、平行线等分线段定理和推论的应用
(1)把线段n等分.
(2)证明在同一直线上的线段相等.
1.判断题
(1)如图四边形ABCD中,点M、N分别在AB、CD上若AM=BM、DN=CN 则AD∥MN∥BC ( )
(2)一组平行线,任意相邻的两平行线间的距离都相等,则这组平行线能等分线段 ( )
(3)如图l1∥l2∥l3且AB=BC,那么AB=BC=DE=EF ( )
2.已知:线段AB, 求作:线段AB的五等分点.
A
B
P
问题1: 求作一点P把线段AB分成2:3?
问题2: 如果把△ABC的面积分成2:3?
3.已知:如图,梯形ABCD中,AD∥BC,∠ABC=90°M是CD的中点.
求证:AM=BM
A
B
C
D
M
证明:过M点作ME∥AD交AB于点E
又∵在梯形ABCD中,MD=MC
∴AE=EB
易证ME是AB的垂直平分线,∴AM=BM
4.利用平行线等分线段定理,证明三角形中位线定理.
D、E 分别是△ABC中AB边和AC边的中点.
求证:DE//BC且
作DE?//BC
作DF//AC
=DE
∴DE//BC且DE=1/2BC.
5.如图:有块直角三角形菜地,分配给张,王,李三家农民耕种,已知张,王,李三家人口分别为2人,4人,6人,菜地分配方法按人口比例,并要求每户土地均有一部分紧靠水渠AB,P处是三家合用的肥料仓库,所以点P必须是三家地的交界地
要求:用尺规在图中作出
各家菜地的分界线.
习题1.1(第5页)
1.设AB的长为6厘米.
(1) 过点A作射线AC;
(2) 在射线AC上以适当的长度顺序截取AD=DE=EF=FG=GH=HK=KM;
(3) 过D、E、F、G、H、K作BM的平行线,分别交AB于点D’、E’、F’、G’、H’、K’.则D’、E’、F’、G’、H’、K’即为线段AB的七等分点.
2.猜想:BE=EF=FD.
证明如图,因为M是AB的中点,N是DC的中点,四边形AB-CD是平行四边形,
所以AM//CN,且AM=CN.
所以四边形ANCN是平行四边形.
所以MC//AN.
即:ME平分BF,即BE=EF.
同理可证:FD=EF.
所以:BE=EF=FD.
3. 如图,因为E,F分别是梯形ABCD中AB、DC边上的中点,所以EF//AD,EF//BC.
所以G、H分别是梯形对角线BD、AC的中点.
所以,EG=1/2AD,FH=1/2AD,EH=1/2BC,FG=1/2BC.
又因为GH=EH-EG,GH=FG-FH,
所以,2GH=EH+FG-(EG+FH)
=1/2BC+1/2BC-(1/2AD+1/2AD)
=BC-AD.
所以,GH=1/2(BC-AD).
