四 直角三角形的射影定理(共18张PPT)
文档属性
| 名称 | 四 直角三角形的射影定理(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 744.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-11 21:33:17 | ||
图片预览





文档简介
(共18张PPT)
阳光照射下,物体都有影子!
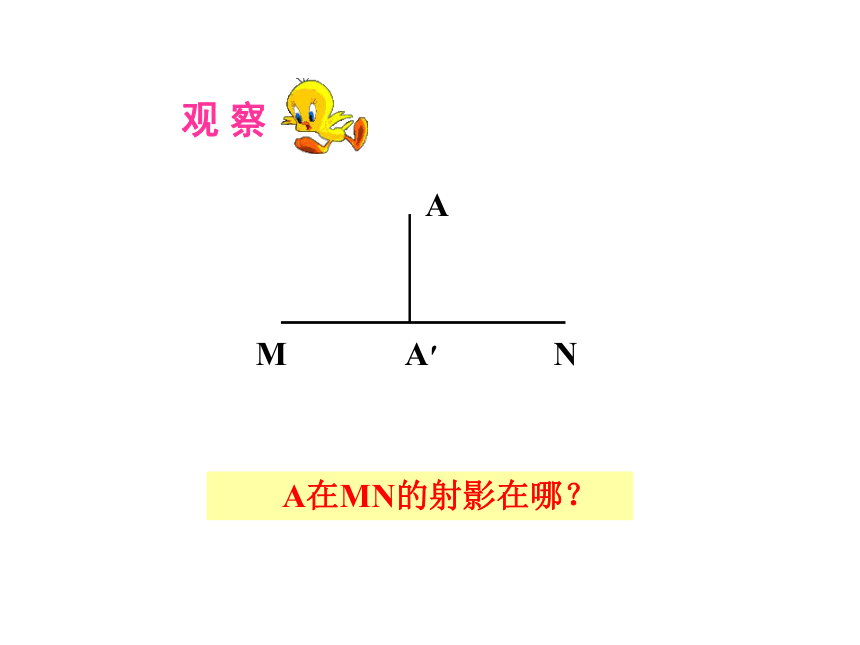
A在MN的射影在哪?
M
N
A
A′
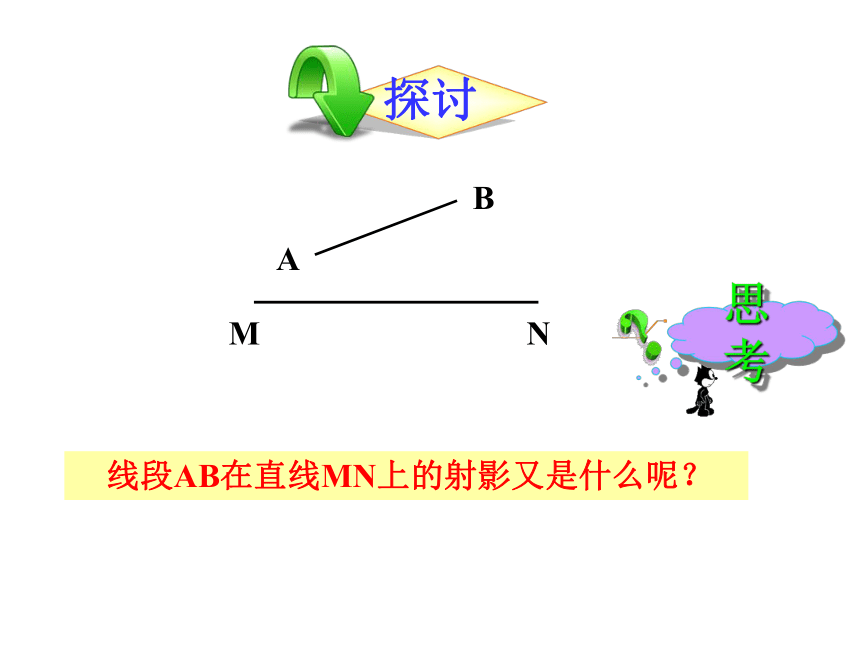
线段AB在直线MN上的射影又是什么呢?
M
N
A
B
1.掌握直角三角形的射影定理.
2.能够利用射影定理求解线段的长.
知识与能力
1.通过日常生活的射影例子,体会并掌握射影定理的定义.
2.培养化归思想,从特殊到一般,再到特殊.
过程与方法
1.通过直角三角形的射影定理,体会并推出一般三角形的射影性质.
2.通过课堂学习培养敢于结合以前所学知识,推导出新的知识或性质,有利于深刻理解.
情感态度与价值观
直角三角形的射影定理.
重点
灵活应用直角三角形的射影定理并能证明.
难点
A ′是点A在MN上的正射影,A ′ B ′是线段AB在MN上的正射影.
找出上图中相似三角形的个数?
考察Rt△ACD和Rt △CBD.
CD是AD、BD的比例中项.
考察Rt△BDC和Rt △BCA.
由(1)(2)(3)反应出直角三角形两直角边在斜边上的射影与其他线段之间的关系.
射影定理:
直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项.
射影定理
直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项.
很重要!
1.已知:Rt△ABC,CD是斜边AB上的高,CD=4,BD=2,
求:AD、AB、AC、BC.
解:
根据射影定理:CD2=AD·BD
∴AD=16÷2=8. ∴AB=AD+BD=10.
∵AC2=AD·AB. ∴AC=4 .
同理BC2=BD·AB. ∴AC=2 .
2. 如图,在△ABC中,CD⊥AB于D,DE⊥AC于E,DF⊥BC于F.
求证:△CEF∽△CBA .
证明:
根据直角三角形的射影定理:CD2=CE·CA;
CD2=CF·CB;
∴CE·CA=CF·CB 即:
又∵∠C是公共角;
根据角边角得: △CEF∽△CBA .
习题1.4(第22页)
阳光照射下,物体都有影子!
A在MN的射影在哪?
M
N
A
A′
线段AB在直线MN上的射影又是什么呢?
M
N
A
B
1.掌握直角三角形的射影定理.
2.能够利用射影定理求解线段的长.
知识与能力
1.通过日常生活的射影例子,体会并掌握射影定理的定义.
2.培养化归思想,从特殊到一般,再到特殊.
过程与方法
1.通过直角三角形的射影定理,体会并推出一般三角形的射影性质.
2.通过课堂学习培养敢于结合以前所学知识,推导出新的知识或性质,有利于深刻理解.
情感态度与价值观
直角三角形的射影定理.
重点
灵活应用直角三角形的射影定理并能证明.
难点
A ′是点A在MN上的正射影,A ′ B ′是线段AB在MN上的正射影.
找出上图中相似三角形的个数?
考察Rt△ACD和Rt △CBD.
CD是AD、BD的比例中项.
考察Rt△BDC和Rt △BCA.
由(1)(2)(3)反应出直角三角形两直角边在斜边上的射影与其他线段之间的关系.
射影定理:
直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项.
射影定理
直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项.
很重要!
1.已知:Rt△ABC,CD是斜边AB上的高,CD=4,BD=2,
求:AD、AB、AC、BC.
解:
根据射影定理:CD2=AD·BD
∴AD=16÷2=8. ∴AB=AD+BD=10.
∵AC2=AD·AB. ∴AC=4 .
同理BC2=BD·AB. ∴AC=2 .
2. 如图,在△ABC中,CD⊥AB于D,DE⊥AC于E,DF⊥BC于F.
求证:△CEF∽△CBA .
证明:
根据直角三角形的射影定理:CD2=CE·CA;
CD2=CF·CB;
∴CE·CA=CF·CB 即:
又∵∠C是公共角;
根据角边角得: △CEF∽△CBA .
习题1.4(第22页)
