人教版九年级数学下册 28.2解直角三角形复习学案(无答案)
文档属性
| 名称 | 人教版九年级数学下册 28.2解直角三角形复习学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 128.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 21:29:19 | ||
图片预览




文档简介
一、目标引领
课题名称:北师大版 九年级 下 数学第23课时《解直角三角形》
达成目标:1.认识锐角三角函数(sinA,cosA,tanA),知道30°,45°,60°角的三角函数值;2.能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题;3.问题解决过程中,体会数形结合、转化思想、方程思想等重要数学思想
课前准备建议:(提示:复习相关知识或思考问题情境)
二、学习指导
录像课 学习经历案(简要把教学过程呈现就行)
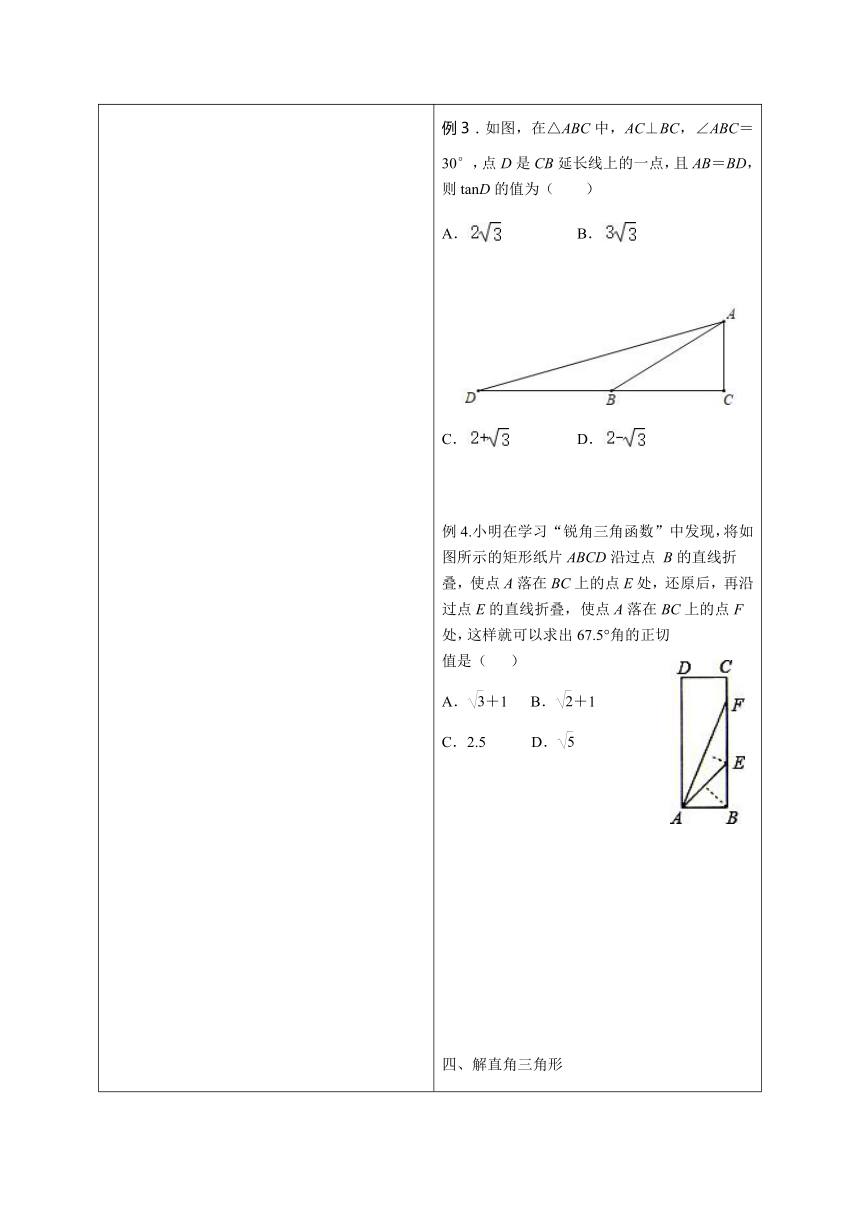
一、课标要求、知识体系、考点呈现、(约3分钟) 二、知识回顾,典型例题(约6分钟) 三、知识回顾,典型例题(约5分钟) 四、知识回顾,典型例题(约7分钟) 五、知识回顾,典型例题(约7分钟) 六、复习小结 (约1分钟) 一、结合济南学考呈现课标要求、知识脉络、历年考点。 二、锐角三角函数(正弦、余弦、正切)1.知识点2.典型例题(一)锐角三角函数例1.如图,在平面直角坐标系中,点P(3,m)是第一象限内的点,且OP与x轴正半轴的夹角α的正切值为,则sinα的值为( )A. B. C. D. 例2.在Rt△ABC中,∠C=90°,sinA=,则cosB的值等于( )A. B. C. D. (二)小方格中的三角函数例1、例2、例3、例4见课件 三、特殊锐角(30°、45°、60°)的三角函数值 1.知识点2.典型例题例1.在△ABC中,若|sin A- |+( -cos B)2=0,∠A,∠B都是锐角,则∠C=________.例2. 若锐角α满足cosα< 且 tanα<,则α的范围是( )A.30°<α<45° B.45°<α<60° C.60°<α<90° D.30°<α<60例3.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且AB=BD,则tanD的值为( )A. B.C. D. 例4.小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点 B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°角的正切值是( )A.+1 B.+1 C.2.5 D. 四、解直角三角形1.知识点2.典型例题例1.如图,在△ABC中,∠ACB=90°,下列结论正确的是( )A.AC=BC?tanA B.AB=AC?cosA C.AC=AB?sinA D.AC=BC?tanB例2.如图,△ABC中,cosB=,sinC=,BC=7,则△ABC的面积为________ 例3.如图,在△ABC中,∠A=90°,sinB=,点D在边AB上,若AD=AC,则tan∠BCD的值为( )A. B.C. D. 五、解直角三角形的实际应用问题1.知识点2.典型例题例1.、例2、例3见课件
当堂检测(课堂检测:根据所讲内容布置5题左右)
1. 如图,在平面直角坐标系中,点A的坐标为(3,4),那么cosα的值是( )A. B. C. D.2.在Rt△ABC中,∠C=90°,若sinA=,则tanA的值是A. B. C. D. 3. 如图,A,B,C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为 . 4. 已知α是锐角,且sin(α+15°)=。计算的值。5.如图所示,小明在家里楼顶上的点A处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A处看电梯楼顶部点B处的仰角为60°,在点A处看这栋电梯楼底部点C处的俯角为45°,两栋楼之间的距离为30m,求电梯楼的高BC
作业布置1.计算:cos245°+sin245°=( )A. B.1 C. D.2.在Rt△ABC中,∠C=90°,若sinA=,则cosB的值等于( )A. B. C. D.13.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则tanB的值是____ 4.如图,在Rt△ABC中,∠C=90°,AB=6,cosB= ,则BC的长为_________5.在△ABC中,若∠A、∠B满足|cosA- |+(sinB- )2=0,则∠C= 6. 如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:≈1.414,≈1.732) 7. (B层)如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).(1)求小敏到旗杆的距离DF.(结果保留根号)(2)求旗杆EF的高度.(结果保留整数,参考数据:≈1.4,≈1.7)
五、总结反思(学生填写)
六、错题纠正(学生填写)
