必修2 1.2空间几何体的三视图、表面积与体积 同步测试题(含答案解析)
文档属性
| 名称 | 必修2 1.2空间几何体的三视图、表面积与体积 同步测试题(含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 380.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-11 14:20:40 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
空间几何体的三视图、表面积与体积 训练测试题
1.某几何体的三视图如图所示,那么这个几何体是( )
INCLUDEPICTURE "D:\\2020版 创新设计 二轮专题复习 学生用书 数学 全国(理)\\4S13.TIF" \* MERGEFORMATINET
A.三棱锥 B.四棱锥
C.四棱台 D.三棱台
2.《九章算术》商功章有题:一圆柱形谷仓,高1丈3尺3寸,容纳米2 000斛(注:1丈=10尺,1尺=10寸,1斛≈1.62立方尺,圆周率取3),则圆柱底面圆周长约为( )
A.1丈3尺 B.5丈4尺
C.9丈2尺 D.48丈6尺
3.如图是棱长为2的正方体的表面展开图,则多面体ABCDE的体积为( )
INCLUDEPICTURE "D:\\2020版 创新设计 二轮专题复习 学生用书 数学 全国(理)\\A12.TIF" \* MERGEFORMATINET
A.2 B.
C. D.
4.若圆锥与球的体积相等,且圆锥底面半径与球的直径相等,则圆锥侧面积与球面面积之比为( )
A.∶2 B.∶2
C.∶2 D.3∶2
5.某几何体的三视图如图所示,则该几何体的体积为( )
INCLUDEPICTURE "D:\\2020版 创新设计 二轮专题复习 学生用书 数学 全国(理)\\L129.tif" \* MERGEFORMATINET
A.6 B.4
C. D.
6.如果一个水平放置的图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )
A.2+ B.
C. D.1+
7.如图所示,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,若VP-ABCD=,则球O的表面积是( )
INCLUDEPICTURE "D:\\2020版 创新设计 二轮专题复习 学生用书 数学 全国(理)\\A14.TIF" \* MERGEFORMATINET
A.4π B.8π
C.12π D.16π
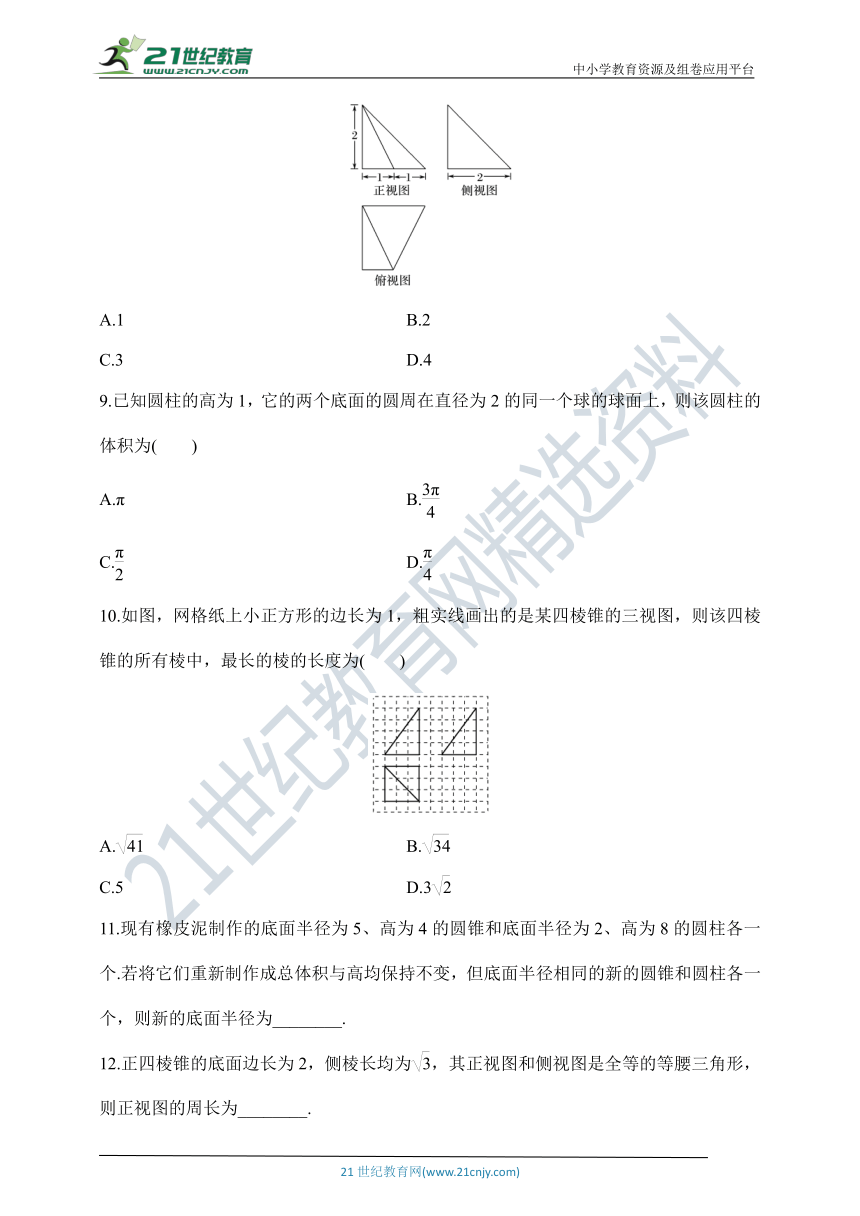
8.某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )
INCLUDEPICTURE "D:\\2020版 创新设计 二轮专题复习 学生用书 数学 全国(理)\\18GS30.tif" \* MERGEFORMATINET
A.1 B.2
C.3 D.4
9.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.π B.
C. D.
10.如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的所有棱中,最长的棱的长度为( )
INCLUDEPICTURE "D:\\2020版 创新设计 二轮专题复习 学生用书 数学 全国(理)\\4S14.TIF" \* MERGEFORMATINET
A. B.
C.5 D.3
11.现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为________.
12.正四棱锥的底面边长为2,侧棱长均为,其正视图和侧视图是全等的等腰三角形,则正视图的周长为________.
INCLUDEPICTURE "D:\\2020版 创新设计 二轮专题复习 学生用书 数学 全国(理)\\5S90.TIF" \* MERGEFORMATINET
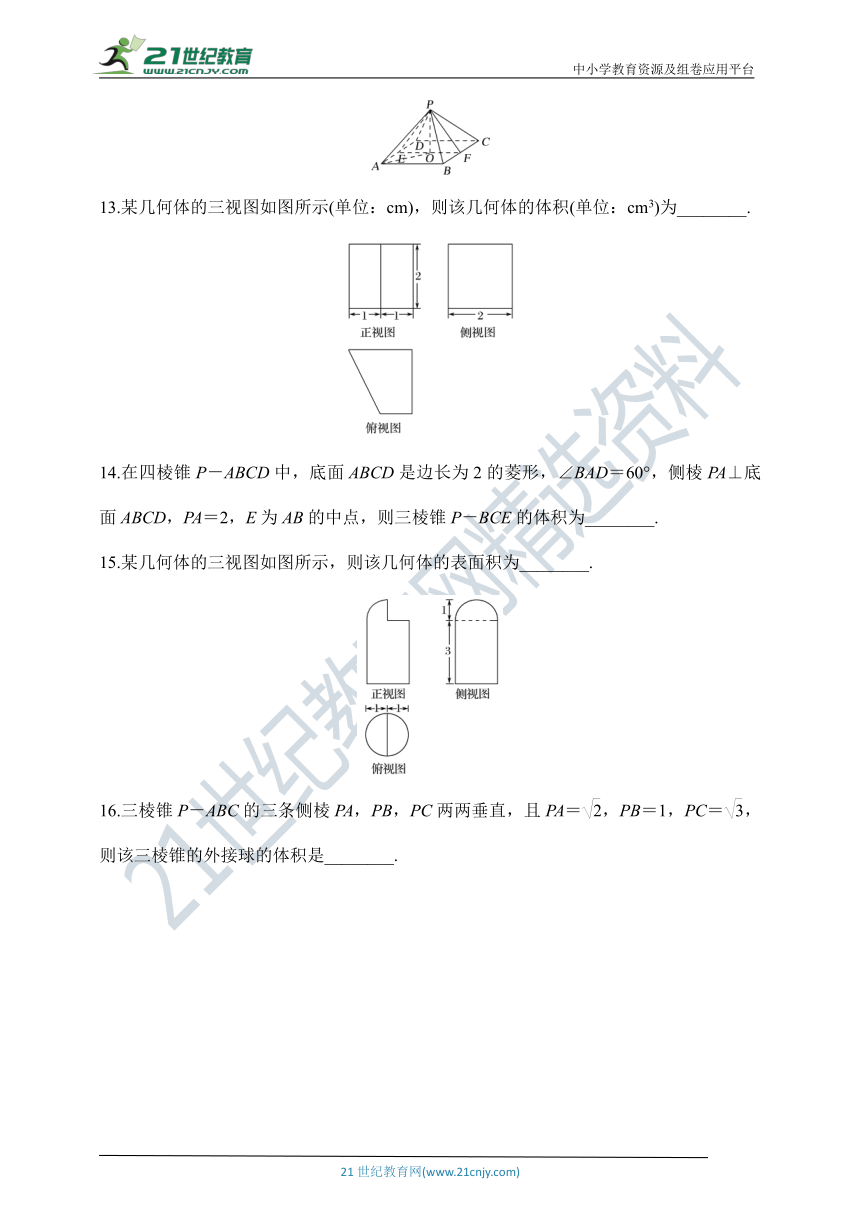
13.某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)为________.
INCLUDEPICTURE "D:\\2020版 创新设计 二轮专题复习 学生用书 数学 全国(理)\\18GS19.tif" \* MERGEFORMATINET
14.在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,PA=2,E为AB的中点,则三棱锥P-BCE的体积为________.
15.某几何体的三视图如图所示,则该几何体的表面积为________.
INCLUDEPICTURE "D:\\2020版 创新设计 二轮专题复习 学生用书 数学 全国(理)\\A15.TIF" \* MERGEFORMATINET
16.三棱锥P-ABC的三条侧棱PA,PB,PC两两垂直,且PA=,PB=1,PC=,则该三棱锥的外接球的体积是________.
答案解析
1.解析 因为正视图和侧视图都为三角形,可知几何体为锥体,又因为俯视图为三角形,故该几何体为三棱锥.
答案 A
2.解析 由题意,圆柱形谷仓的高h=10+3+×=(尺),体积V≈2 000×1.62=3 240(立方尺).设圆柱的底面半径为R尺,由体积公式得πR2×≈3 240,得3R2×≈3 240,解得R2≈81,故R≈9,所以底面圆周长C=2πR≈2×3×9=54(尺),即5丈4尺.
答案 B
3.解析 多面体ABCDE为四棱锥(如图),利用割补法可得其体积V=4-=.
INCLUDEPICTURE "D:\\2020版 创新设计 二轮专题复习 学生用书 数学 全国(理)\\A13.TIF" \* MERGEFORMATINET
答案 D
4.解析 设圆锥底面半径为r,高为h,则球的半径R=,
由条件知,πr2h=π,所以h=.
所以圆锥的侧面积S1=πr·=πr=πr2,球面面积S2=4πR2=4π×=πr2,
所以S1∶S2=∶2.
答案 C
5.解析 由三视图知该几何体是边长为2的正方体挖去一个三棱柱(如图),且挖去的三棱柱的高为1,底面是边长为2的等腰直角三角形,故几何体体积V=23-×2×2×1=6.
INCLUDEPICTURE "D:\\2020版 创新设计 二轮专题复习 学生用书 数学 全国(理)\\L129A.tif" \* MERGEFORMATINET
答案 A
6.解析 恢复后的原图形为一直角梯形,
所以S=(1++1)×2=2+.
答案 A
7.解析 由OP=OC=R,AB=R,得AB2·OP=×(R)2×R=,所以R=2.
∴S球=4πR2=16π.
答案 D
8.解析 在正方体中作出该几何体的直观图,记为四棱锥P-ABCD,如图,由图可知在此四棱锥的侧面中,直角三角形的个数为3.
INCLUDEPICTURE "D:\\2020版 创新设计 二轮专题复习 学生用书 数学 全国(理)\\18GW37.TIF" \* MERGEFORMATINET
答案 C
9.解析 如图画出圆柱的轴截面ABCD,O为球心.球半径R=OA=1,球心到底面圆的距离为OM=.
∴底面圆半径r=AM==,故圆柱体积V=π·r2·h=π·×1=.
INCLUDEPICTURE "D:\\2020版 创新设计 二轮专题复习 学生用书 数学 全国(理)\\B2A.TIF" \* MERGEFORMATINET
答案 B
10.解析 由三视图可知该几何体为如图所示的四棱锥P-ABCD.
INCLUDEPICTURE "D:\\2020版 创新设计 二轮专题复习 学生用书 数学 全国(理)\\4S15.TIF" \* MERGEFORMATINET
其中PA⊥底面ABCD,四棱锥P-ABCD的底面是边长为3的正方形,高PA=4.
连接AC,易知最长的棱为PC,且PC===.
答案 B
11.解析 设新的底面半径为r,由题意得πr2·4+πr2·8=π×52×4+π×22×8,解得r=.
答案
12.解析 由题意知,正视图就是如图所示的截面PEF,其中E,F分别是AD,BC的中点,连接AO,易得AO=,又PA=,于是解得PO=1,所以PE=,故其正视图的周长为2+2.
答案 2+2
13.解析 由三视图可知,该几何体是一个底面为直角梯形的直四棱柱,所以该几何体的体积V=×(1+2)×2×2=6.
答案 6
14.解析 由题意知S△EBC=×2×1×sin 120°=,故VP-EBC=×2×=.
答案
15.解析 由三视图可得该几何体为圆柱和四分之一球的组合体.圆柱的底面半径为1,高为3,球的半径为1.
故该几何体的表面积为S=π×12+2π×1×3+4π×12×+π×12+π×12=9π.
答案 9π
16.解析 三棱锥P-ABC的三条侧棱PA,PB,PC两两互相垂直,它的外接球就是它扩展为长方体的外接球,求出长方体的对角线的长为=,所以球的直径是,半径为.
球的体积为V=×π×=π.
答案 π
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
