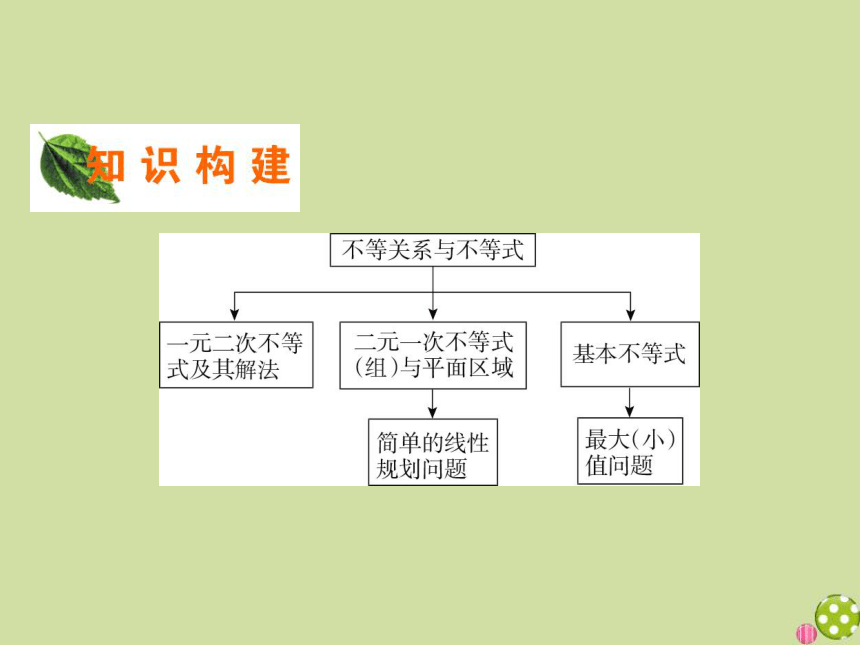
2019_2020学年高中数学第三章不等式章末归纳整合课件(37张ppt)新人教A版必修5
文档属性
| 名称 | 2019_2020学年高中数学第三章不等式章末归纳整合课件(37张ppt)新人教A版必修5 |  | |
| 格式 | zip | ||
| 文件大小 | 795.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 12:10:24 | ||
图片预览









文档简介
(共37张PPT)
章末归纳整合
不等式与函数、方程三者密不可分、相互转化,有关求参数的取值范围,实际应用问题等,都要考虑函数与方程思想.
函数与方程思想
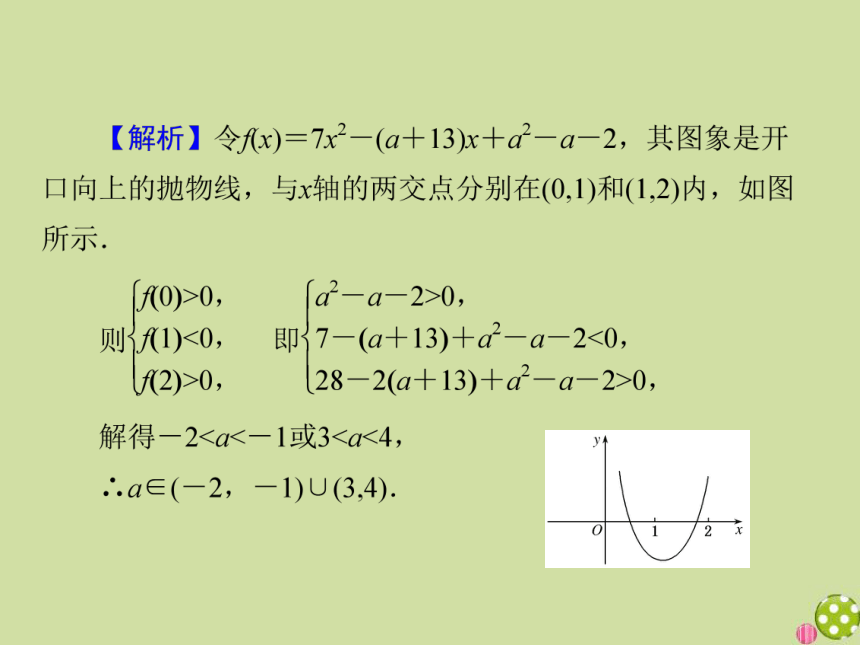
【例1】 设a∈R,关于x的不等式7x2-(a+13)x+a2-a-2<0的解集为(α,β)且0<α<1<β<2,求a的取值范围.
【分析】利用二次函数的图象解答.
【点评】不等式、函数与方程有着密切的联系,它们之间可以相互转化,尤其是函数的图象直观、形象,有助于不等式、方程求解.
【点评】本题主要考查一元二次方程根的分布问题,通过与函数、不等式的联系来求解,也体现了转化与化归、数形结合的思想.
方程x2+(m-2)x+5-m=0的两根都大于2,则m的取值范围是( )
A.(-5,-4] B.(-∞,-4]
C.(-∞,-2] D.(-∞,-5)∪(-5,-4]
【答案】A
解含有字母的不等式时,往往要对其中所含的字母进行适当的分类讨论,分类讨论的原因一般有以下两种:一是对不等式作等价变换时,正确运用不等式的性质而引起讨论;二是对不等式作等价变换时,由相应函数单调性的可能变化而引起的讨论.
分类讨论思想
【例3】 解关于x的不等式ax2-x-(a+1)<0.
【分析】讨论a=0时,a>0时,a<0时,原不等式的解集情况,从而求出答案来.
【点评】本题考查了含有字母系数的不等式的解法问题,解题时应对字母系数进行分类讨论,是易错题.
解关于x的不等式x2-(2+a)x+2a<0.
【解析】不等式x2-(2+a)x+2a<0可化为
(x-2)(x-a)<0,
所以,当a=2时,不等式为(x-2)2<0,解集为?;
当a>2时,不等式的解集为{x|2<x<a};
当a<2时,不等式的解集为{x|a<x<2}.
数学以现实世界的数量关系和空间形式作为其研究的对象,而数与形是相互联系、相互制约的,在一定条件下是可以相互转化的.
数形结合思想
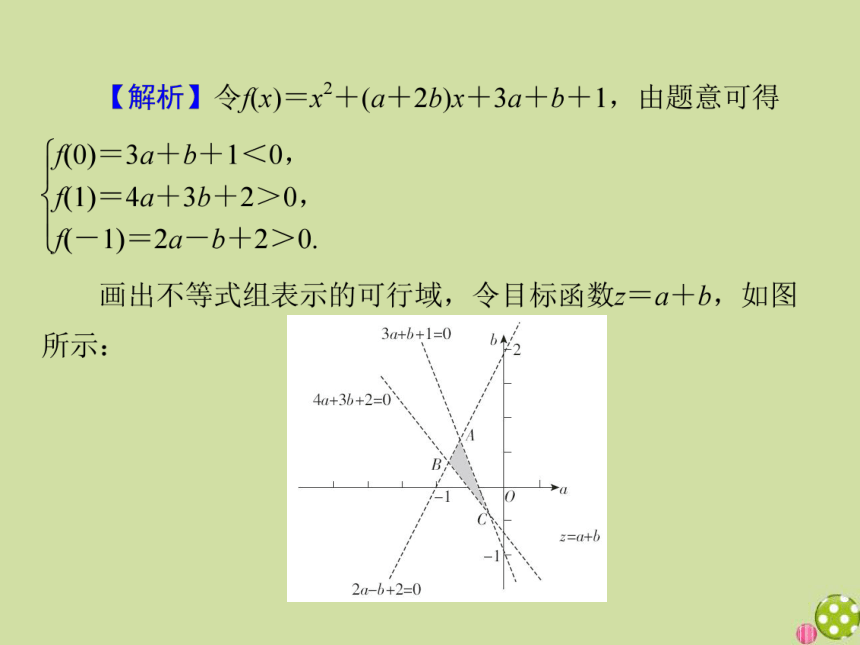
【解析】如图,可行域为一个三角形,验证知在点A(1,2)时,z1=x+y+5取得最大值8,∴z最大是3,故选B.
不等与相等是相对的,在一定条件下可以相互转化,解题过程就是一个由已知条件向待定结论等价转化的过程,无论是哪种类型的不等式,其求解过程及其思路都是等价转化.
转化与化归思想
【例5】 已知函数f(x)=32x-(k+1)·3x+2,当x∈R时,f(x)>0,求实数k的取值范围.
【分析】f(x)不是二次函数,但令t=3x,则f(x)可转化为二次函数,可进一步求解.
已知不等式x2-2x+a>0对任意实数x∈[2,3]恒成立,则实数a的取值范围为__________.
【答案】(0,+∞)
【解析】令f(x)=x2-2x+a=(x-1)2+a-1,∴f(x)在区间(1,+∞)上单调递增.又不等式x2-2x+a>0对任意实数x∈[2,3]恒成立,∴f(2)>0,即4-4+a>0,解得a>0.故实数a的取值范围是(0,+∞).
本章内容有三个高频考点:一元二次不等式的解法,简单的线性规划,基本不等式求最值.这一部分内容有时会贯穿其他章节中,或者是单独命题,考查形式是以选择或者填空的形式出现,解决此类问题需要借助于等价转化、分类讨论等数学思想.
5.(2017年江苏)某公司一年购买某种货物600吨,每次购买x吨,运费为6万元/次,一年的总存储费用为4x万元.要使一年的总运费与总存储费用之和最小,则x的值是________.
【答案】30
6.(2018年江苏)在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为________.
【答案】9
章末归纳整合
不等式与函数、方程三者密不可分、相互转化,有关求参数的取值范围,实际应用问题等,都要考虑函数与方程思想.
函数与方程思想
【例1】 设a∈R,关于x的不等式7x2-(a+13)x+a2-a-2<0的解集为(α,β)且0<α<1<β<2,求a的取值范围.
【分析】利用二次函数的图象解答.
【点评】不等式、函数与方程有着密切的联系,它们之间可以相互转化,尤其是函数的图象直观、形象,有助于不等式、方程求解.
【点评】本题主要考查一元二次方程根的分布问题,通过与函数、不等式的联系来求解,也体现了转化与化归、数形结合的思想.
方程x2+(m-2)x+5-m=0的两根都大于2,则m的取值范围是( )
A.(-5,-4] B.(-∞,-4]
C.(-∞,-2] D.(-∞,-5)∪(-5,-4]
【答案】A
解含有字母的不等式时,往往要对其中所含的字母进行适当的分类讨论,分类讨论的原因一般有以下两种:一是对不等式作等价变换时,正确运用不等式的性质而引起讨论;二是对不等式作等价变换时,由相应函数单调性的可能变化而引起的讨论.
分类讨论思想
【例3】 解关于x的不等式ax2-x-(a+1)<0.
【分析】讨论a=0时,a>0时,a<0时,原不等式的解集情况,从而求出答案来.
【点评】本题考查了含有字母系数的不等式的解法问题,解题时应对字母系数进行分类讨论,是易错题.
解关于x的不等式x2-(2+a)x+2a<0.
【解析】不等式x2-(2+a)x+2a<0可化为
(x-2)(x-a)<0,
所以,当a=2时,不等式为(x-2)2<0,解集为?;
当a>2时,不等式的解集为{x|2<x<a};
当a<2时,不等式的解集为{x|a<x<2}.
数学以现实世界的数量关系和空间形式作为其研究的对象,而数与形是相互联系、相互制约的,在一定条件下是可以相互转化的.
数形结合思想
【解析】如图,可行域为一个三角形,验证知在点A(1,2)时,z1=x+y+5取得最大值8,∴z最大是3,故选B.
不等与相等是相对的,在一定条件下可以相互转化,解题过程就是一个由已知条件向待定结论等价转化的过程,无论是哪种类型的不等式,其求解过程及其思路都是等价转化.
转化与化归思想
【例5】 已知函数f(x)=32x-(k+1)·3x+2,当x∈R时,f(x)>0,求实数k的取值范围.
【分析】f(x)不是二次函数,但令t=3x,则f(x)可转化为二次函数,可进一步求解.
已知不等式x2-2x+a>0对任意实数x∈[2,3]恒成立,则实数a的取值范围为__________.
【答案】(0,+∞)
【解析】令f(x)=x2-2x+a=(x-1)2+a-1,∴f(x)在区间(1,+∞)上单调递增.又不等式x2-2x+a>0对任意实数x∈[2,3]恒成立,∴f(2)>0,即4-4+a>0,解得a>0.故实数a的取值范围是(0,+∞).
本章内容有三个高频考点:一元二次不等式的解法,简单的线性规划,基本不等式求最值.这一部分内容有时会贯穿其他章节中,或者是单独命题,考查形式是以选择或者填空的形式出现,解决此类问题需要借助于等价转化、分类讨论等数学思想.
5.(2017年江苏)某公司一年购买某种货物600吨,每次购买x吨,运费为6万元/次,一年的总存储费用为4x万元.要使一年的总运费与总存储费用之和最小,则x的值是________.
【答案】30
6.(2018年江苏)在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为________.
【答案】9
