2019_2020学年高中数学新人教A版必修5第一章解三角形章末归纳整合课件(共29张PPT)
文档属性
| 名称 | 2019_2020学年高中数学新人教A版必修5第一章解三角形章末归纳整合课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 772.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 12:16:30 | ||
图片预览





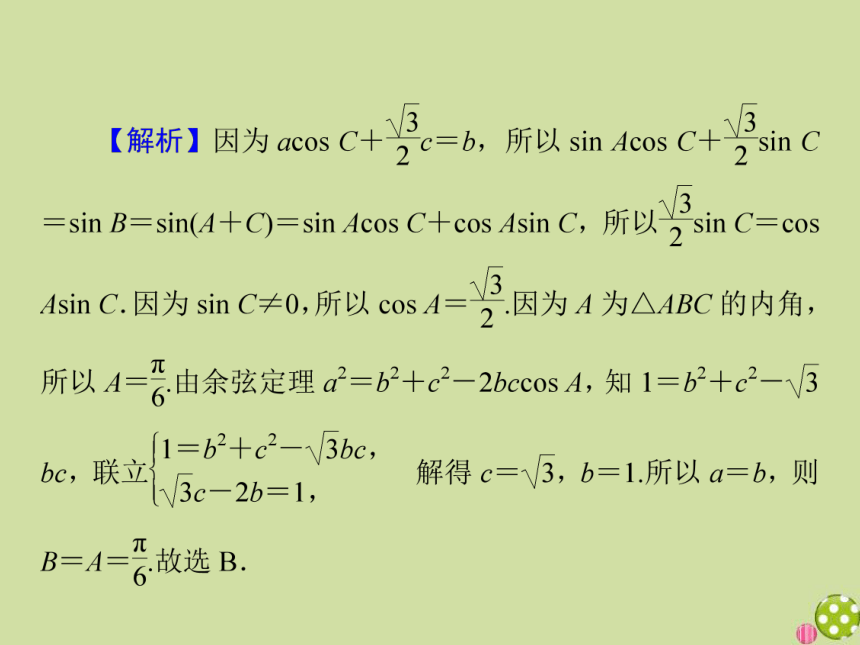


文档简介
(共29张PPT)
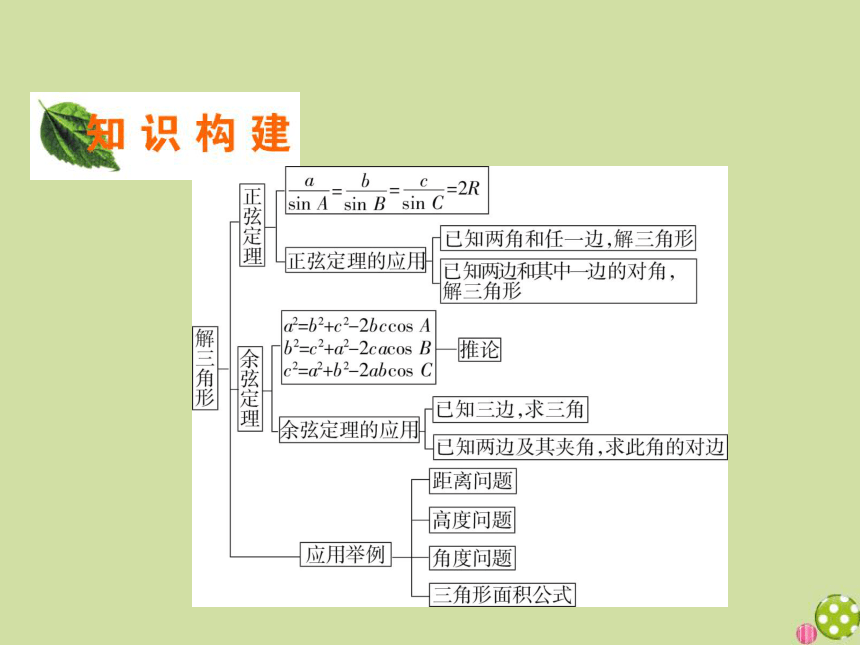
章末归纳整合
函数的思想就是运用变化的观点分析和研究具体问题中的数量关系.在具体问题中把变量之间的关系用函数表示出来,然后用函数的观点研究问题.本章中主要借助二次函数来研究距离和速度的最值问题.
方程的思想就是在解决问题时,用事先设定的未知数沟通问题中所涉及的各量间的制约关系,列出方程(组),从而求出未知数及各量的值.正弦定理、余弦定理在一定条件下都可以看作方程,从而求出所需要的量.
函数与方程思想
【点评】本题考查利用数学知识解决实际问题,考查余弦定理,考查学生的计算能力,比较基础.
当数学问题不能用统一形式解决时,可以把已知条件的范围划分为若干个子集,在各个子集内分别讨论问题的解,然后综合各类解而得到原问题的答案.这种解决问题的思想方法叫做分类讨论的思想方法.如正弦定理的证明(对三角形分别是直角三角形、锐角三角形、钝角三角形逐一讨论,并将锐角三角形、钝角三角形转化为直角三角形),解三角形中解的个数等,通过讨论,将不可能的或与题设条件不相符的逐一排除,从而得出正确结论,讨论时要做到不重不漏.
分类讨论思想
【例2】 如图所示,A,B两个小岛相距21 n mile,B岛在A岛的正南方,现在甲船从A岛出发,以9 n mile/h的速度向B岛行驶,而乙船同时以6 n mile/h的速度离开B岛沿南偏东60°方向行驶,问行驶多长时间后,两船相距最近?并求出两船的最近距离.
【解析】设行驶t小时后,甲船行驶了9t n mile到达C处,乙船行驶了6t n mile到达D处.
一些问题直接求解比较困难,需将原问题转化为一个自己熟悉的易于求解的问题,这就是转化与化归的思想.在本章中,将所求面积转化为三角形面积问题,将实际问题转化为数学问题等,都是转化与化归思想的具体应用.
转化与化归思想
【例3】 (2019年河南郑州模拟)△ABC的内角A,B,C的对边分别为a,b,c,已知B=2C,2b=3c.
(1)求cos C;
(2)若c=4,求△ABC的面积.
以正弦定理,余弦定理的直接应用为主要考查目标,可能以选择题、填空题或解答题形式出现,多为中等难度.考查形式主要与三角变换相结合,直接在三角形中以处理边、角关系的形式呈现,以实际问题为背景,结合向量或几何知识构建综合性题也是可能的发展方向.
2.(2017年山东)在△ABC中,角A,B,C的对边分别为a,b,c.若△ABC为锐角三角形,且满足sin B(1+2cos C)=2sin Acos C+cos Asin C,则下列等式成立的是( )
A.a=2b B.b=2a
C.A=2B D.B=2A
【答案】A
【解析】由题意知sin(A+C)+2sin Bcos C=2sin A·cos C+cos Asin C,所以2sin Bcos C=sin Acos C?2sin B=sin A?2b=a.故选A.
4.(2015年湖北)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600 m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=________m.
章末归纳整合
函数的思想就是运用变化的观点分析和研究具体问题中的数量关系.在具体问题中把变量之间的关系用函数表示出来,然后用函数的观点研究问题.本章中主要借助二次函数来研究距离和速度的最值问题.
方程的思想就是在解决问题时,用事先设定的未知数沟通问题中所涉及的各量间的制约关系,列出方程(组),从而求出未知数及各量的值.正弦定理、余弦定理在一定条件下都可以看作方程,从而求出所需要的量.
函数与方程思想
【点评】本题考查利用数学知识解决实际问题,考查余弦定理,考查学生的计算能力,比较基础.
当数学问题不能用统一形式解决时,可以把已知条件的范围划分为若干个子集,在各个子集内分别讨论问题的解,然后综合各类解而得到原问题的答案.这种解决问题的思想方法叫做分类讨论的思想方法.如正弦定理的证明(对三角形分别是直角三角形、锐角三角形、钝角三角形逐一讨论,并将锐角三角形、钝角三角形转化为直角三角形),解三角形中解的个数等,通过讨论,将不可能的或与题设条件不相符的逐一排除,从而得出正确结论,讨论时要做到不重不漏.
分类讨论思想
【例2】 如图所示,A,B两个小岛相距21 n mile,B岛在A岛的正南方,现在甲船从A岛出发,以9 n mile/h的速度向B岛行驶,而乙船同时以6 n mile/h的速度离开B岛沿南偏东60°方向行驶,问行驶多长时间后,两船相距最近?并求出两船的最近距离.
【解析】设行驶t小时后,甲船行驶了9t n mile到达C处,乙船行驶了6t n mile到达D处.
一些问题直接求解比较困难,需将原问题转化为一个自己熟悉的易于求解的问题,这就是转化与化归的思想.在本章中,将所求面积转化为三角形面积问题,将实际问题转化为数学问题等,都是转化与化归思想的具体应用.
转化与化归思想
【例3】 (2019年河南郑州模拟)△ABC的内角A,B,C的对边分别为a,b,c,已知B=2C,2b=3c.
(1)求cos C;
(2)若c=4,求△ABC的面积.
以正弦定理,余弦定理的直接应用为主要考查目标,可能以选择题、填空题或解答题形式出现,多为中等难度.考查形式主要与三角变换相结合,直接在三角形中以处理边、角关系的形式呈现,以实际问题为背景,结合向量或几何知识构建综合性题也是可能的发展方向.
2.(2017年山东)在△ABC中,角A,B,C的对边分别为a,b,c.若△ABC为锐角三角形,且满足sin B(1+2cos C)=2sin Acos C+cos Asin C,则下列等式成立的是( )
A.a=2b B.b=2a
C.A=2B D.B=2A
【答案】A
【解析】由题意知sin(A+C)+2sin Bcos C=2sin A·cos C+cos Asin C,所以2sin Bcos C=sin Acos C?2sin B=sin A?2b=a.故选A.
4.(2015年湖北)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600 m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=________m.
