人教版七下数学 5.2.2平行线的判定 课件 (51张PPT)
文档属性
| 名称 | 人教版七下数学 5.2.2平行线的判定 课件 (51张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 973.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 16:42:25 | ||
图片预览





文档简介
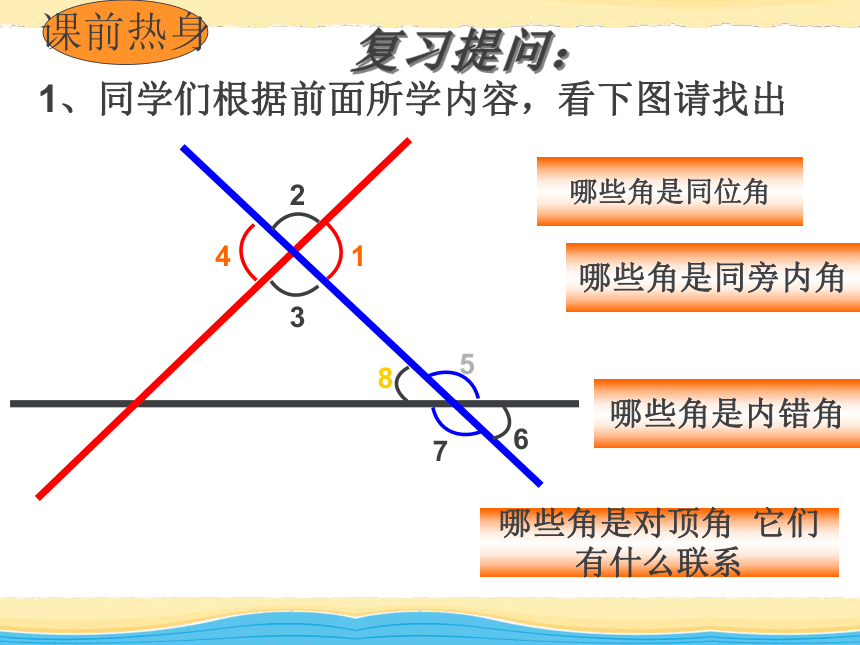
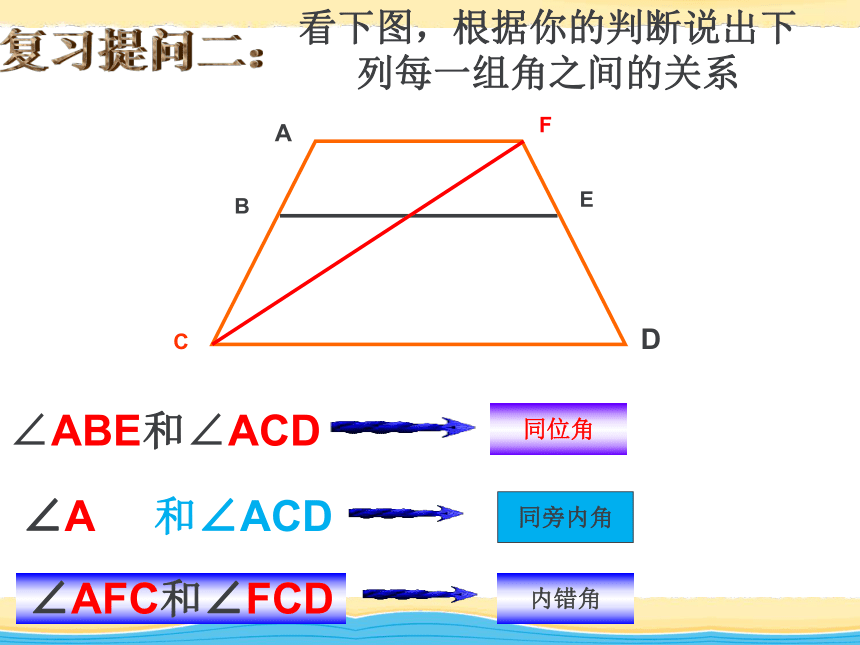
课件51张PPT。平行线的判定 平行线的判定1、同学们根据前面所学内容,看下图请找出哪些角是内错角哪些角是同位角哪些角是同旁内角哪些角是对顶角 它们有什么联系23415786复习提问:课前热身看下图,根据你的判断说出下列每一组角之间的关系∠ABE和∠ACD ∠A 和∠ACD∠AFC和∠FCD同位角同旁内角内错角复习提问二:判断下列语句是否正确:(1) 两条直线不相交,就叫做平行线. ( )(2) 与一条直线平行的直线只有一条. ( )(3) 如果两条直线a、b都和直线c平行,
那么直线a、b就平行. ( )×√×热身训练 判定两条直线平行的方法有两种:定义:在同一平面内,不相交的两条直线叫平行线。平行公理的推论同学们可以想一想?
除应用以上两种方法以外,是否还有其它方法呢?如果两条直线同平行于一条直线,那么两条直线平行。 12观察思考
讨论交流ab.A1、画图过程中直尺起到了什么作用? ∠1和∠2是什么位置关系的角?
2、在三角板移动的过程中,∠1和∠2的大小发生变化了吗?
3、要判断a//b你有办法了吗?
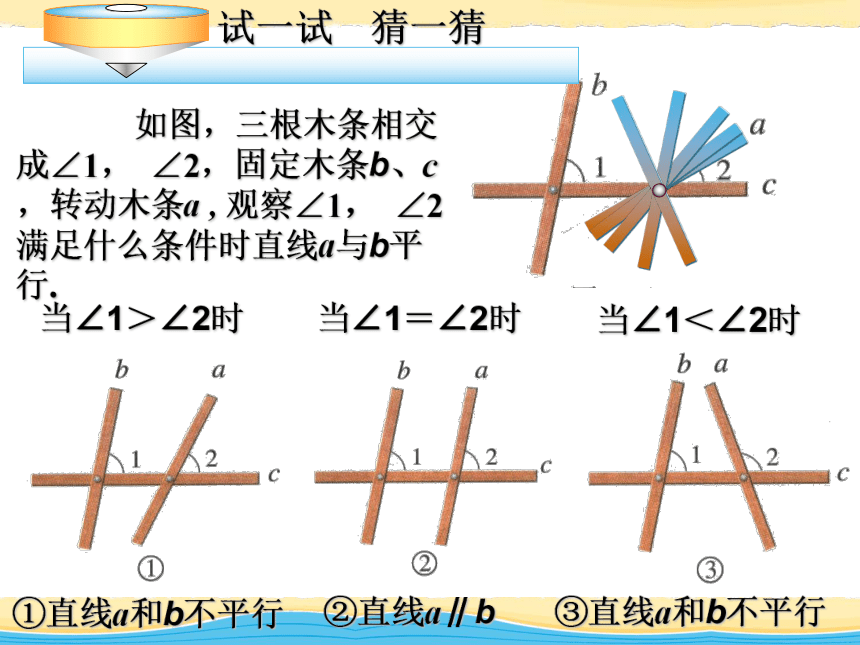
如图,三根木条相交成∠1, ∠2,固定木条b、c,转动木条a , 观察∠1, ∠2满足什么条件时直线a与b平行.当∠1=∠2时①直线a和b不平行②直线a∥b③直线a和b不平行 两条直线被第三条直线所截,如果同
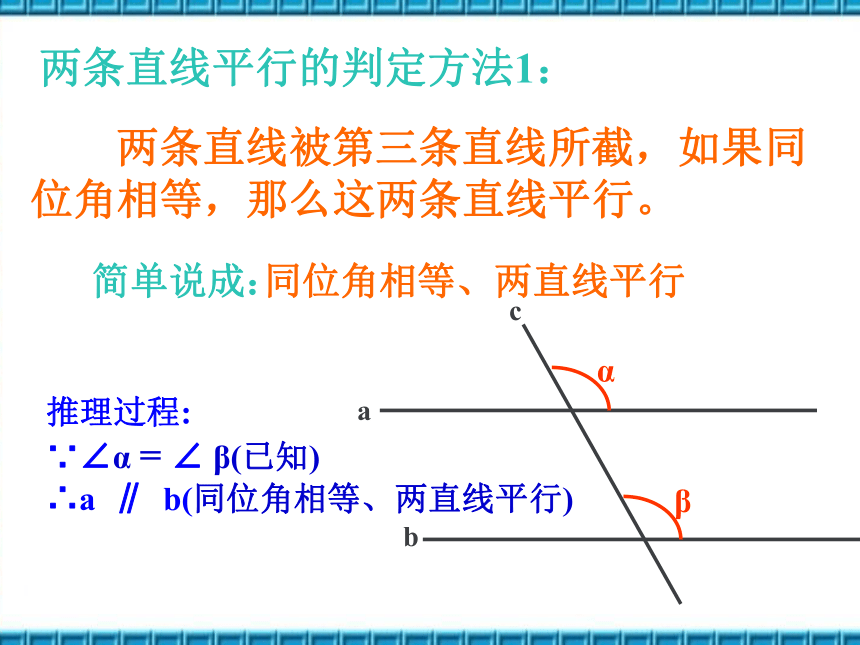
位角相等,那么这两条直线平行。简单说成:同位角相等、两直线平行两条直线平行的判定方法1:推理过程:
∵∠α = ∠ β(已知)
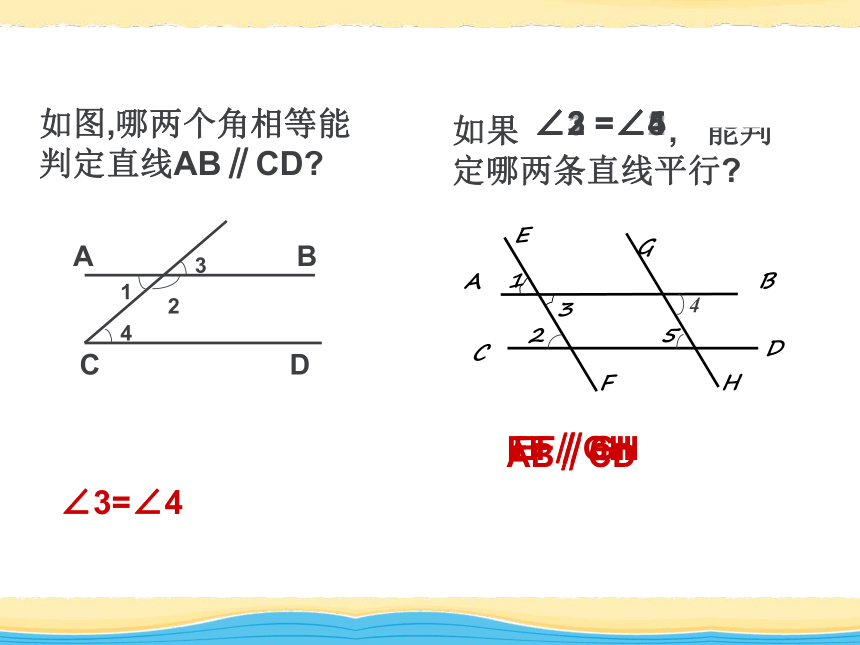
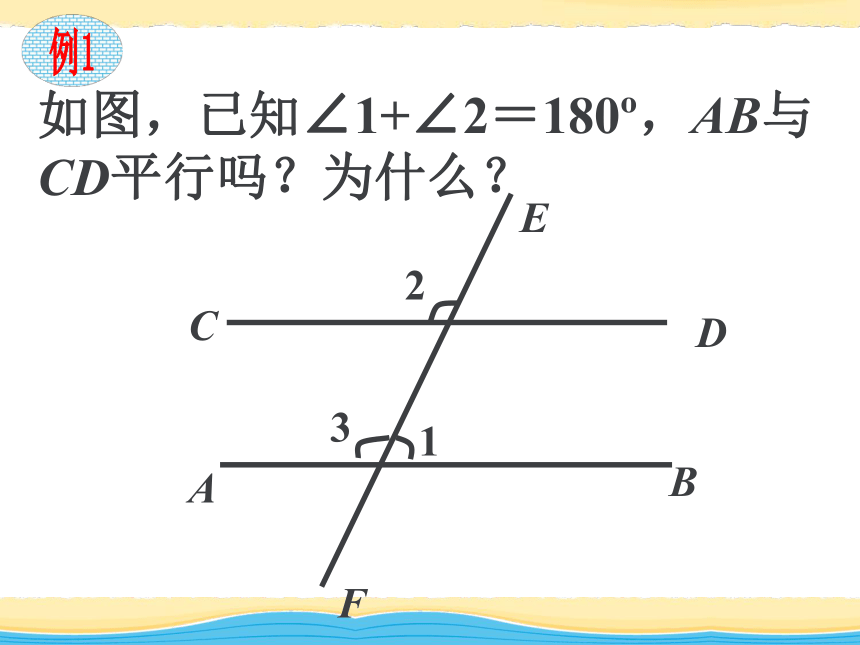
∴a ∥ b(同位角相等、两直线平行)如图,哪两个角相等能判定直线AB∥CD?如果 , 能判定哪两条直线平行? ∠1 =∠2∠3=∠4AB∥CDEF∥GH∠3 =∠4∠2 =∠5EF∥GH如图,已知∠1+∠2=180o,AB与CD平行吗?为什么?ABCDEF123Zx.xk 2 已知:如图,ABC、CDE都是直线, 且∠1=∠2,∠1=∠C,
求证:AC∥FD.
∵ ∠1 = ∠2,
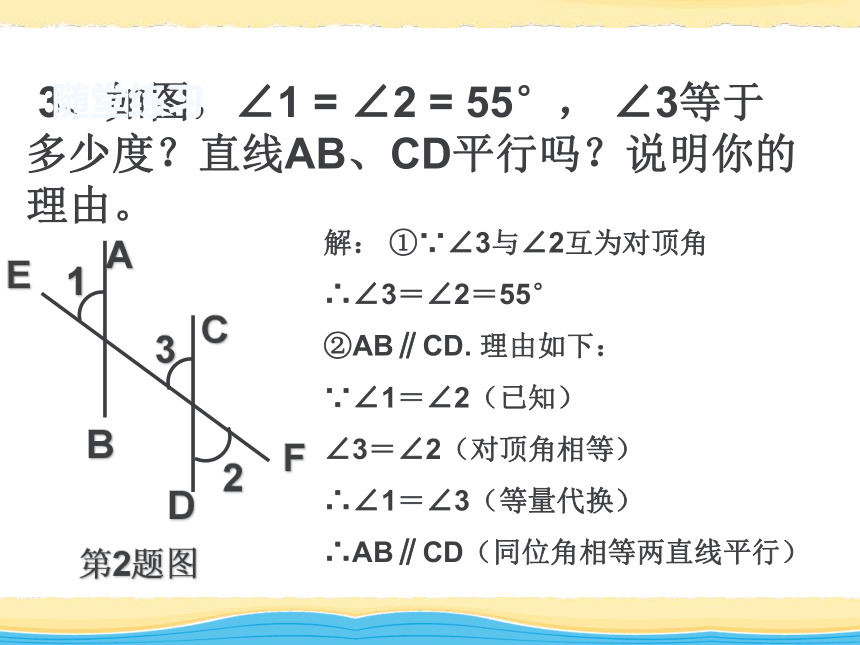
∠1 = ∠C (已知) ∴ ∠2=∠C (等量代换) ∴ AC∥FD (同位角相等,两直线平行) FEBCDA21证明: 3、如图,∠1 = ∠2 = 55°, ∠3等于
多少度?直线AB、CD平行吗?说明你的
理由。第2题图312ABFCDE随堂练习解: ①∵∠3与∠2互为对顶角
∴∠3=∠2=55°
②AB∥CD. 理由如下:
∵∠1=∠2(已知)
∠3=∠2(对顶角相等)
∴∠1=∠3(等量代换)
∴AB∥CD(同位角相等两直线平行)如图,已知∠1=∠2,AB与CD平行吗?为什么?ABCDEF12两条直线平行的判定方法2: 两条直线被第三条直线所截 ,如果内错角相等, 那么这两条直线平行.简单地说,内错角相等,两直线平行.如图,哪两个角相等能判定直线AB∥CD?如果 , 能判定哪两条直线平行? ∠3 =∠2∠3=∠4或∠1=∠4AB∥CDAB∥CD∠5 =∠6∠4 =∠5EF∥GH6直线a、b被直线l所截,已知∠1=1150 ∠2=1150,问直线a和直线b平行吗?为什么
解:a ∥b
∵∠1=1150 ∠2=1150∴∠1=∠2∴a∥b﹙内错角相等,两直线平行﹚例4 已知:如图,∠DAB被AC平分,
且∠1=∠3,
ABCD123求证:AB∥CD.
∵ ∠DAB被AC平分 (已知) ∴ ∠1=∠2 (角平分线定义) ∵ ∠1=∠3 (已知) ∴ ∠2=∠3 (等量代换) ∴ AB∥CD ( 内错角相等,两直线平行 ) 证明:已知∠3=45 °,∠1与∠2互余,试求出 ? 解:由于∠1与∠2是对顶角,
∴∠1=∠2
又∵∠1+∠2=90°(已知)
∴∠1=∠2=45°
∵ ∠3=45°(已知)
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)看谁高手AB//CD如图,已知∠1+∠2=180o,AB与CD平行吗?为什么?ABCDEF12两条直线平行的判定方法3: 两条直线被第三条直线所截 ,如果同旁内角互补, 那么这两条直线平行.简单地说,同旁内角互补,两直线平行. 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?∵ b⊥a∴∠2=90° (垂直的定义)∴b∥c. (同位角相等,两直线平行)∴∠1=90° (垂直的定义)∵ c ⊥a∴∠1=∠2想一想理由:平行理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)abc12方法2:理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)abc12方法3:结论在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线平行。bca1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.在同一平面内,如果两条直线都垂直于
同一条直线,那么这两条直线平行。
6.平行线的定义判定两条直线是否平行的方法有:判定两直线平行有哪些方法? 1.当∠1 与∠2有什么关系时 , a∥b?为什么? ababba121212Zx.xk ∵∠B= ∠1(已知) ∴____∥_____( ) 1ABDC∵∠D= ∠1(已知)
∴____∥_____( ) ADBC同位角相等,两直线平行ABDC内错角相等,两直线平行2.如图,3.如图,
① ∵∠B= ∠C(已知)
∴______∥______
( ) ② ∵∠D+∠BCD=1800 (已知)
∴_______∥________
( )
内错角相等,两直线平行EABCDADBC 同旁内角互补,两直线平行(1)∵∠1 =∠4(已知)
∴____∥____( )
(2)∵∠___= ∠___(已知)
∴BC ∥ EF( )
(3) ∵∠1= ∠___(已知)
∴DE ∥____( )练习4 GCFEBHDA4123GHBC23内错角相等,两直线平行内错角相等,两直线平行2AB内错角相等,两直线平行(1)∵∠A+∠D=180°
∴____∥____( )
(2) ∵∠____+ ∠____=180°
∴AD ∥ ___ ( )ADCBABCD 同旁内角互补,两直线平行DCBC 同旁内角互补,两直线平行练习4 5、如图:当∠ABH= 时,AB∥DE
当∠ABE + =180°时,AB∥DE
当∠HBC= 时,BC ∥EF
当∠GBC= 时,BC ∥EF∠DEH∠DEB∠FEH∠GEF (1)如图1,∠C=57°,
当∠ABE= °时,就能使BE∥CD. (2)如图2 , ∠1=120°,∠2=60°.
问a与b的关系? 图1图2a∥b ABECD12ab 573c能力挑战:(A)∠2=∠3 (B)∠1=∠4
(C)∠1=∠2 (D)∠1=∠3 D能力挑战:8、如图,∠1=∠2,则下列结论正确的是( )(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BCC知识应用1、如图,有一座山,想从山中开凿一条隧道直通甲、乙两地;在甲地侧得乙为北偏东41.5o方向,如果甲、乙两地同时开工,那么从乙地出发应按北偏西 度施工。乙地2、一弯形轨道ABCD的拐角?ABC=120o,那么当另一拐角? BCD= o时,AB??CD3、如图,在屋架上要加一根横梁DE,若?ABC=33o,那么?ADE= 时才能使DE ??BC。138.56033°3、用两块相同的三角板按如图所示的方式作平行线,能解释其中道理的依据是 。4、一学员在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )(A)第一次向右拐50o,第二次向左拐130o
(B)第一次向左拐30o,第二次向右拐30o
(C)第一次向右拐50o,第二次向右拐130o
(D)第一次向左拐50o,第二次向左拐130o内错角相等,两直线平行B7、如图,a∥c,∠1=∠2,那么c∥b吗?解:∵ ∠1=∠2( )∴ a∥b( ) ∵ a∥c( )∴ c∥b( )如图:直线AB、CD都和AE相交,
且∠1+∠A=180o .
求证:AB//CDCBAD21E 证明:∵∠1+∠A=180o3练习∴∠2+∠A=180o∴( )( )( )( )已知对顶角相等等量代换同旁内角互补,
两直线平行∠1=∠2AB∥CD9.某人骑自行车从 A 地出发,沿正东方向前进至 B 处后,右转 150,沿直线向前行驶到C处,这时他想仍按正东方向?请画出他应怎样调整行驶的路线,并说明理由.能力挑战:12、如图,哪些直线平行,哪些直线不平行?例2:如图,AB⊥CD于点B,AE与BF相交于点G,且∠FGE=60°, ∠ABG=30°。请判断AE与CD是否平行,并说明理由。例3.如图所示,直线MN分别和直线AB, CD,EF相交于G,H,P, ∠1=∠2,∠2+∠3=180°试问:AB与EF平行吗?为什么?ABCDEFMGHP321例4 已知:如图,∠1=∠C,∠2=∠B,
求证:MN∥EF.
∵ ∠1=∠C (已知) ∴ MN∥BC (内错角相等,两直线平行) ∵ ∠2=∠B (已知) ∴ EF∥BC (同位角相等,两直线平行) ∴ MN∥EF (平行于同一直线的两条直线平行) FEMNA21BC证明: 如图,直线EF交直线AB、CD于点M、N,∠EMB= ∠END,MG平分∠EMB ,NH平分∠END,试问:图中哪两条直线互相平行?
为什么?F例5、7、如图,AF、CE、BD交于点B,且BE平分∠DBF,且∠1= ∠C,问BD与AC平行吗?为什么?考考你8、如图,BC、DE分别平分?ABD和?BDF,且?1=?2,请找出平行线,并说明理由。21ABDFCE考考你9、如图,AB、CD被EF所截,MG平分∠BMN,NH平分∠DNM,已知∠GMN+ ∠HNM=90°,试问:AB∥CD吗?请说明理由。E考考你10.已知BE平分∠ABC,∠1= ∠3,DE与BC平行吗?为什么?如果DF平分∠ADE, 你能说明图中那两条直线平行?为什么?FC1G11.已知∠1=∠3,∠2与∠3互补,那么可以判断哪几组直线互相平行?答:有两组平行线,分别是AB?DE,BC? EFABBC12如图, ∠C+∠A= ∠ AEC,判断AB与CD是否平行,并说明理由ABCDE思考Q3.如图11,直线AB、CD被EF所截,∠1 =∠2,∠CNF =∠BME。求证:AB∥CD,MP∥NQ.
2.如图10,∠1∶∠2∶∠3 = 2∶3∶4, ∠AFE = 60°,∠BDE =120°,写出图中平行的直线,并说明理由.
1.如图9,∠D =∠A,∠B =∠FCB,
求证:ED∥CF.
那么直线a、b就平行. ( )×√×热身训练 判定两条直线平行的方法有两种:定义:在同一平面内,不相交的两条直线叫平行线。平行公理的推论同学们可以想一想?
除应用以上两种方法以外,是否还有其它方法呢?如果两条直线同平行于一条直线,那么两条直线平行。 12观察思考
讨论交流ab.A1、画图过程中直尺起到了什么作用? ∠1和∠2是什么位置关系的角?
2、在三角板移动的过程中,∠1和∠2的大小发生变化了吗?
3、要判断a//b你有办法了吗?
如图,三根木条相交成∠1, ∠2,固定木条b、c,转动木条a , 观察∠1, ∠2满足什么条件时直线a与b平行.当∠1=∠2时①直线a和b不平行②直线a∥b③直线a和b不平行 两条直线被第三条直线所截,如果同
位角相等,那么这两条直线平行。简单说成:同位角相等、两直线平行两条直线平行的判定方法1:推理过程:
∵∠α = ∠ β(已知)
∴a ∥ b(同位角相等、两直线平行)如图,哪两个角相等能判定直线AB∥CD?如果 , 能判定哪两条直线平行? ∠1 =∠2∠3=∠4AB∥CDEF∥GH∠3 =∠4∠2 =∠5EF∥GH如图,已知∠1+∠2=180o,AB与CD平行吗?为什么?ABCDEF123Zx.xk 2 已知:如图,ABC、CDE都是直线, 且∠1=∠2,∠1=∠C,
求证:AC∥FD.
∵ ∠1 = ∠2,
∠1 = ∠C (已知) ∴ ∠2=∠C (等量代换) ∴ AC∥FD (同位角相等,两直线平行) FEBCDA21证明: 3、如图,∠1 = ∠2 = 55°, ∠3等于
多少度?直线AB、CD平行吗?说明你的
理由。第2题图312ABFCDE随堂练习解: ①∵∠3与∠2互为对顶角
∴∠3=∠2=55°
②AB∥CD. 理由如下:
∵∠1=∠2(已知)
∠3=∠2(对顶角相等)
∴∠1=∠3(等量代换)
∴AB∥CD(同位角相等两直线平行)如图,已知∠1=∠2,AB与CD平行吗?为什么?ABCDEF12两条直线平行的判定方法2: 两条直线被第三条直线所截 ,如果内错角相等, 那么这两条直线平行.简单地说,内错角相等,两直线平行.如图,哪两个角相等能判定直线AB∥CD?如果 , 能判定哪两条直线平行? ∠3 =∠2∠3=∠4或∠1=∠4AB∥CDAB∥CD∠5 =∠6∠4 =∠5EF∥GH6直线a、b被直线l所截,已知∠1=1150 ∠2=1150,问直线a和直线b平行吗?为什么
解:a ∥b
∵∠1=1150 ∠2=1150∴∠1=∠2∴a∥b﹙内错角相等,两直线平行﹚例4 已知:如图,∠DAB被AC平分,
且∠1=∠3,
ABCD123求证:AB∥CD.
∵ ∠DAB被AC平分 (已知) ∴ ∠1=∠2 (角平分线定义) ∵ ∠1=∠3 (已知) ∴ ∠2=∠3 (等量代换) ∴ AB∥CD ( 内错角相等,两直线平行 ) 证明:已知∠3=45 °,∠1与∠2互余,试求出 ? 解:由于∠1与∠2是对顶角,
∴∠1=∠2
又∵∠1+∠2=90°(已知)
∴∠1=∠2=45°
∵ ∠3=45°(已知)
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)看谁高手AB//CD如图,已知∠1+∠2=180o,AB与CD平行吗?为什么?ABCDEF12两条直线平行的判定方法3: 两条直线被第三条直线所截 ,如果同旁内角互补, 那么这两条直线平行.简单地说,同旁内角互补,两直线平行. 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?∵ b⊥a∴∠2=90° (垂直的定义)∴b∥c. (同位角相等,两直线平行)∴∠1=90° (垂直的定义)∵ c ⊥a∴∠1=∠2想一想理由:平行理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)abc12方法2:理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)abc12方法3:结论在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线平行。bca1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.在同一平面内,如果两条直线都垂直于
同一条直线,那么这两条直线平行。
6.平行线的定义判定两条直线是否平行的方法有:判定两直线平行有哪些方法? 1.当∠1 与∠2有什么关系时 , a∥b?为什么? ababba121212Zx.xk ∵∠B= ∠1(已知) ∴____∥_____( ) 1ABDC∵∠D= ∠1(已知)
∴____∥_____( ) ADBC同位角相等,两直线平行ABDC内错角相等,两直线平行2.如图,3.如图,
① ∵∠B= ∠C(已知)
∴______∥______
( ) ② ∵∠D+∠BCD=1800 (已知)
∴_______∥________
( )
内错角相等,两直线平行EABCDADBC 同旁内角互补,两直线平行(1)∵∠1 =∠4(已知)
∴____∥____( )
(2)∵∠___= ∠___(已知)
∴BC ∥ EF( )
(3) ∵∠1= ∠___(已知)
∴DE ∥____( )练习4 GCFEBHDA4123GHBC23内错角相等,两直线平行内错角相等,两直线平行2AB内错角相等,两直线平行(1)∵∠A+∠D=180°
∴____∥____( )
(2) ∵∠____+ ∠____=180°
∴AD ∥ ___ ( )ADCBABCD 同旁内角互补,两直线平行DCBC 同旁内角互补,两直线平行练习4 5、如图:当∠ABH= 时,AB∥DE
当∠ABE + =180°时,AB∥DE
当∠HBC= 时,BC ∥EF
当∠GBC= 时,BC ∥EF∠DEH∠DEB∠FEH∠GEF (1)如图1,∠C=57°,
当∠ABE= °时,就能使BE∥CD. (2)如图2 , ∠1=120°,∠2=60°.
问a与b的关系? 图1图2a∥b ABECD12ab 573c能力挑战:(A)∠2=∠3 (B)∠1=∠4
(C)∠1=∠2 (D)∠1=∠3 D能力挑战:8、如图,∠1=∠2,则下列结论正确的是( )(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BCC知识应用1、如图,有一座山,想从山中开凿一条隧道直通甲、乙两地;在甲地侧得乙为北偏东41.5o方向,如果甲、乙两地同时开工,那么从乙地出发应按北偏西 度施工。乙地2、一弯形轨道ABCD的拐角?ABC=120o,那么当另一拐角? BCD= o时,AB??CD3、如图,在屋架上要加一根横梁DE,若?ABC=33o,那么?ADE= 时才能使DE ??BC。138.56033°3、用两块相同的三角板按如图所示的方式作平行线,能解释其中道理的依据是 。4、一学员在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )(A)第一次向右拐50o,第二次向左拐130o
(B)第一次向左拐30o,第二次向右拐30o
(C)第一次向右拐50o,第二次向右拐130o
(D)第一次向左拐50o,第二次向左拐130o内错角相等,两直线平行B7、如图,a∥c,∠1=∠2,那么c∥b吗?解:∵ ∠1=∠2( )∴ a∥b( ) ∵ a∥c( )∴ c∥b( )如图:直线AB、CD都和AE相交,
且∠1+∠A=180o .
求证:AB//CDCBAD21E 证明:∵∠1+∠A=180o3练习∴∠2+∠A=180o∴( )( )( )( )已知对顶角相等等量代换同旁内角互补,
两直线平行∠1=∠2AB∥CD9.某人骑自行车从 A 地出发,沿正东方向前进至 B 处后,右转 150,沿直线向前行驶到C处,这时他想仍按正东方向?请画出他应怎样调整行驶的路线,并说明理由.能力挑战:12、如图,哪些直线平行,哪些直线不平行?例2:如图,AB⊥CD于点B,AE与BF相交于点G,且∠FGE=60°, ∠ABG=30°。请判断AE与CD是否平行,并说明理由。例3.如图所示,直线MN分别和直线AB, CD,EF相交于G,H,P, ∠1=∠2,∠2+∠3=180°试问:AB与EF平行吗?为什么?ABCDEFMGHP321例4 已知:如图,∠1=∠C,∠2=∠B,
求证:MN∥EF.
∵ ∠1=∠C (已知) ∴ MN∥BC (内错角相等,两直线平行) ∵ ∠2=∠B (已知) ∴ EF∥BC (同位角相等,两直线平行) ∴ MN∥EF (平行于同一直线的两条直线平行) FEMNA21BC证明: 如图,直线EF交直线AB、CD于点M、N,∠EMB= ∠END,MG平分∠EMB ,NH平分∠END,试问:图中哪两条直线互相平行?
为什么?F例5、7、如图,AF、CE、BD交于点B,且BE平分∠DBF,且∠1= ∠C,问BD与AC平行吗?为什么?考考你8、如图,BC、DE分别平分?ABD和?BDF,且?1=?2,请找出平行线,并说明理由。21ABDFCE考考你9、如图,AB、CD被EF所截,MG平分∠BMN,NH平分∠DNM,已知∠GMN+ ∠HNM=90°,试问:AB∥CD吗?请说明理由。E考考你10.已知BE平分∠ABC,∠1= ∠3,DE与BC平行吗?为什么?如果DF平分∠ADE, 你能说明图中那两条直线平行?为什么?FC1G11.已知∠1=∠3,∠2与∠3互补,那么可以判断哪几组直线互相平行?答:有两组平行线,分别是AB?DE,BC? EFABBC12如图, ∠C+∠A= ∠ AEC,判断AB与CD是否平行,并说明理由ABCDE思考Q3.如图11,直线AB、CD被EF所截,∠1 =∠2,∠CNF =∠BME。求证:AB∥CD,MP∥NQ.
2.如图10,∠1∶∠2∶∠3 = 2∶3∶4, ∠AFE = 60°,∠BDE =120°,写出图中平行的直线,并说明理由.
1.如图9,∠D =∠A,∠B =∠FCB,
求证:ED∥CF.
