人教版七年级数学下册5.2.2平行线的判定课件( 共17张PPT)
文档属性
| 名称 | 人教版七年级数学下册5.2.2平行线的判定课件( 共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
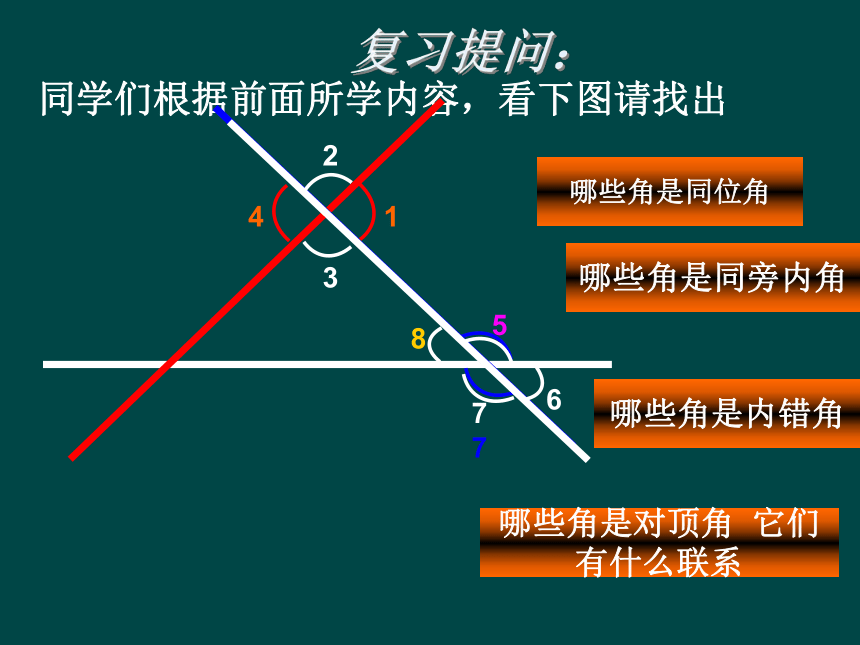
同学们根据前面所学内容,看下图请找出
哪些角是内错角
哪些角是同位角
哪些角是同旁内角
哪些角是对顶角 它们有什么联系
2
3
4
1
5
77
8
6
复习提问
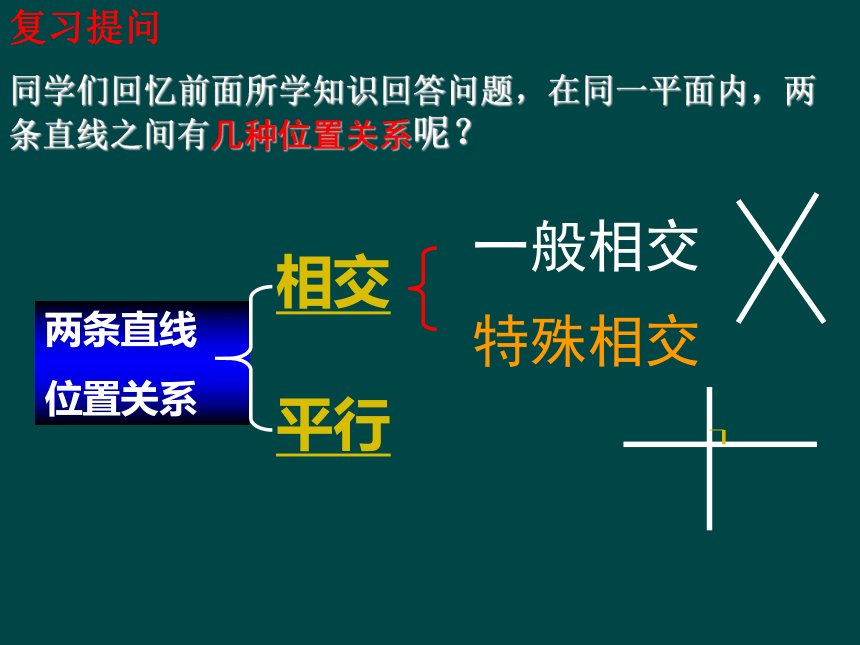
同学们回忆前面所学知识回答问题,在同一平面内,两条直线之间有几种位置关系呢?
一般相交
特殊相交
两条直线
位置关系
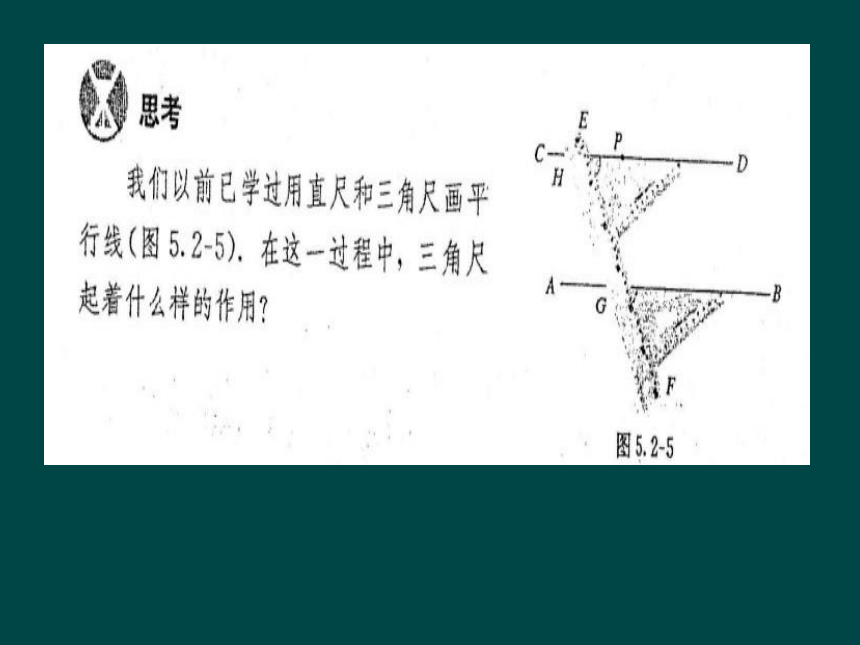
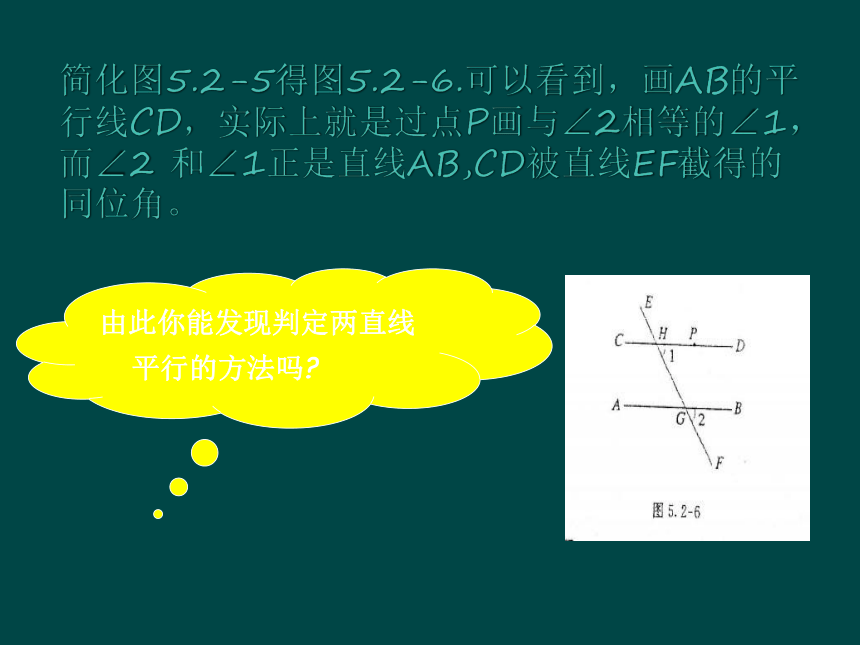
由此你能发现判定两直线平行的方法吗?
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行.
平行线判定方法1:
几何语言表述:
∵∠1=∠2(已知)
∴AB∥CD
(同位角相等,两直线平行)
简单说成:同位角相等,两直线平行。
因为∠2= ∠3,而∠3= ∠1(对顶角相等),所以∠1= ∠2,即同位角相等,从而a∥b。这样根据判定方法1得出判定两直线平行的另一种方法。
简单说成: 内错角相等,两直线平行.
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
平行线判定方法2
符号语言:
∵ ∠3=∠2(已知)
∴ a∥b
(内错角相等,两直线平行)
如图,如果∠2+ ∠3=180 o,那么AB∥CD 吗?为什么?
探究
分析:图中, ∠3+∠1=180 。
∠2+ ∠3=180。
我们得到∠1=
∠2
AB∥CD
两条直线被第三条直线所截 ,如果同旁内角互补, 那么这两条直线平行.
简单说成:
同旁内角互补,两直线平行。
例:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
答:垂直于同一条直线的两条直线平行.
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(同位角相等,两直线平行)
a
b
c
1
2
能力挑战:
(A)∠2=∠3 (B)∠1=∠4
(C)∠1=∠2 (D)∠1=∠3
D
能力挑战:
2、如图,∠1=∠2,则下列结论正确的是( )
(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BC
C
平行线判定方法1:同位角相等,两直线平行。
平行线判定方法2:内错角相等,两直线平行。
平行线判定方法3:同旁内角互补,两直线平行。
教材p16 2、4题
同学们根据前面所学内容,看下图请找出
哪些角是内错角
哪些角是同位角
哪些角是同旁内角
哪些角是对顶角 它们有什么联系
2
3
4
1
5
77
8
6
复习提问
同学们回忆前面所学知识回答问题,在同一平面内,两条直线之间有几种位置关系呢?
一般相交
特殊相交
两条直线
位置关系
由此你能发现判定两直线平行的方法吗?
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行.
平行线判定方法1:
几何语言表述:
∵∠1=∠2(已知)
∴AB∥CD
(同位角相等,两直线平行)
简单说成:同位角相等,两直线平行。
因为∠2= ∠3,而∠3= ∠1(对顶角相等),所以∠1= ∠2,即同位角相等,从而a∥b。这样根据判定方法1得出判定两直线平行的另一种方法。
简单说成: 内错角相等,两直线平行.
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
平行线判定方法2
符号语言:
∵ ∠3=∠2(已知)
∴ a∥b
(内错角相等,两直线平行)
如图,如果∠2+ ∠3=180 o,那么AB∥CD 吗?为什么?
探究
分析:图中, ∠3+∠1=180 。
∠2+ ∠3=180。
我们得到∠1=
∠2
AB∥CD
两条直线被第三条直线所截 ,如果同旁内角互补, 那么这两条直线平行.
简单说成:
同旁内角互补,两直线平行。
例:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
答:垂直于同一条直线的两条直线平行.
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(同位角相等,两直线平行)
a
b
c
1
2
能力挑战:
(A)∠2=∠3 (B)∠1=∠4
(C)∠1=∠2 (D)∠1=∠3
D
能力挑战:
2、如图,∠1=∠2,则下列结论正确的是( )
(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BC
C
平行线判定方法1:同位角相等,两直线平行。
平行线判定方法2:内错角相等,两直线平行。
平行线判定方法3:同旁内角互补,两直线平行。
教材p16 2、4题
