人教版数学八年级上册11.2 与三角形有关的角课件(共27张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.2 与三角形有关的角课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 17:27:45 | ||
图片预览



文档简介
(共27张PPT)
三角形的内角和
同学们,你们知道“三角形
内角和等于180度”这个结论
最早是谁提出的吗?
数学史话
帕斯卡:(1623—1662)法国著名的数学家
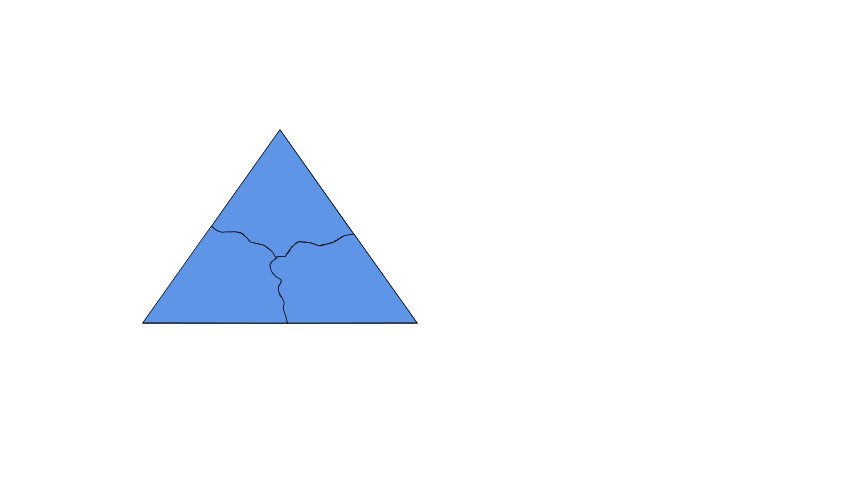
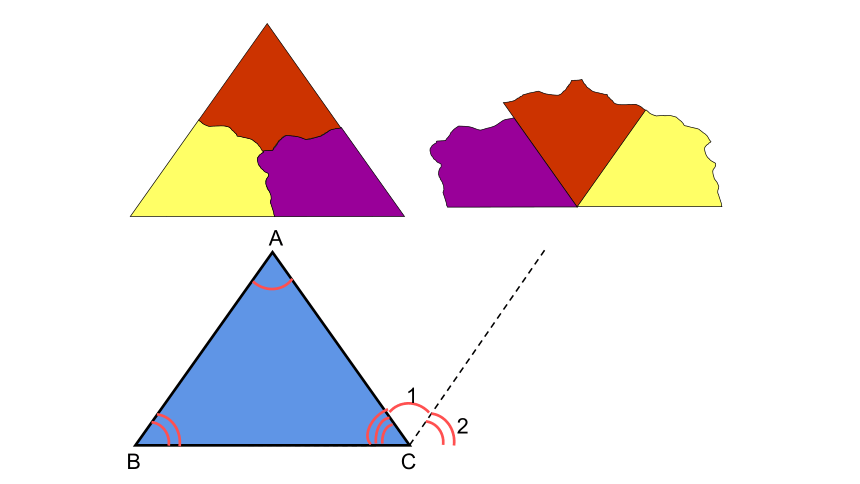
方法:度量、剪拼、折叠
问题1 在小学我们已经知道任意一个三角形三个内角的和等于180°,你还记得是怎么发现这个结论的吗?请大家利用手中的三角形纸片进行探究.
实验操作,探究新知
B
A
C
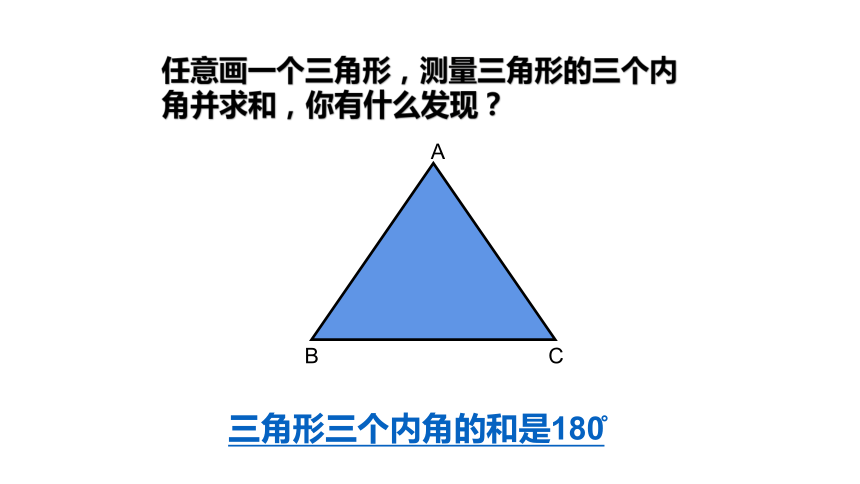
任意画一个三角形,测量三角形的三个内角并求和,你有什么发现?
三角形三个内角的和是180?
1
2
B
A
C
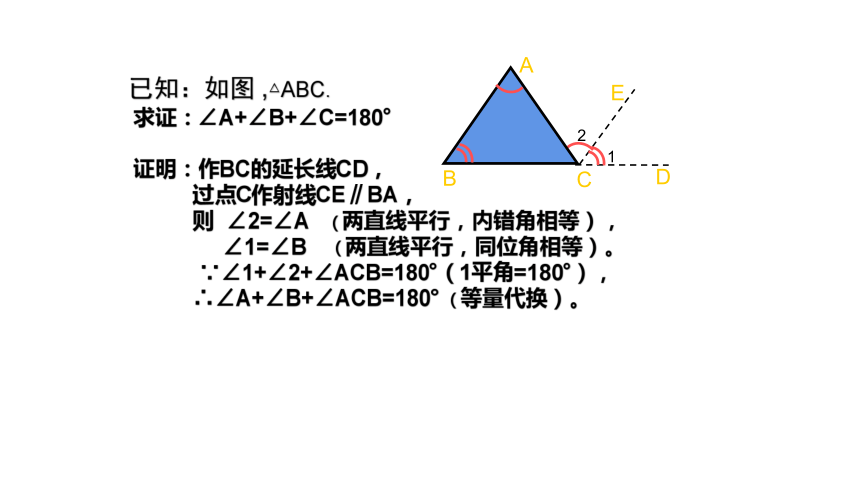
已知:如图 ,△ABC.
求证:∠A+∠B+∠C=180°
证明:作BC的延长线CD,
过点C作射线CE∥BA,
则 ∠2=∠A (两直线平行,内错角相等),
∠1=∠B (两直线平行,同位角相等)。
∵∠1+∠2+∠ACB=180°(1平角=180°),
∴∠A+∠B+∠ACB=180° (等量代换)。
B
A
C
1
2
D
E
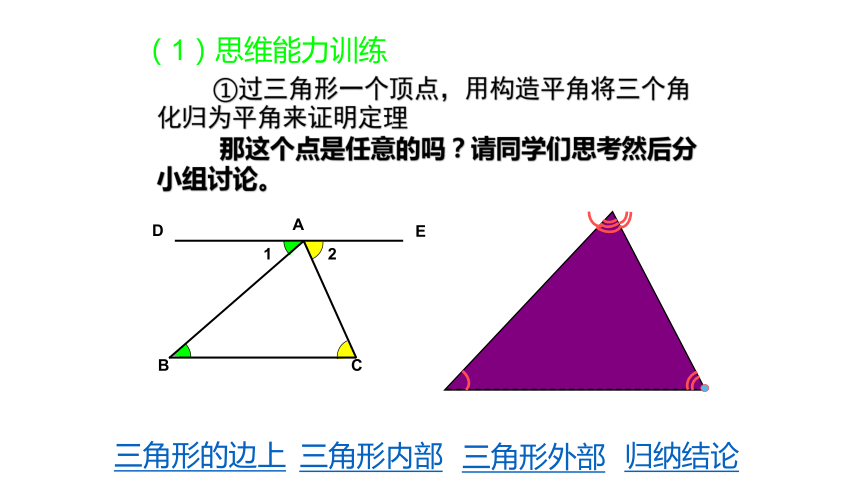
①过三角形一个顶点,用构造平角将三个角化归为平角来证明定理
那这个点是任意的吗?请同学们思考然后分小组讨论。
(1)思维能力训练
2
1
A
B
C
D
E
三角形的边上
三角形内部
三角形外部
归纳结论
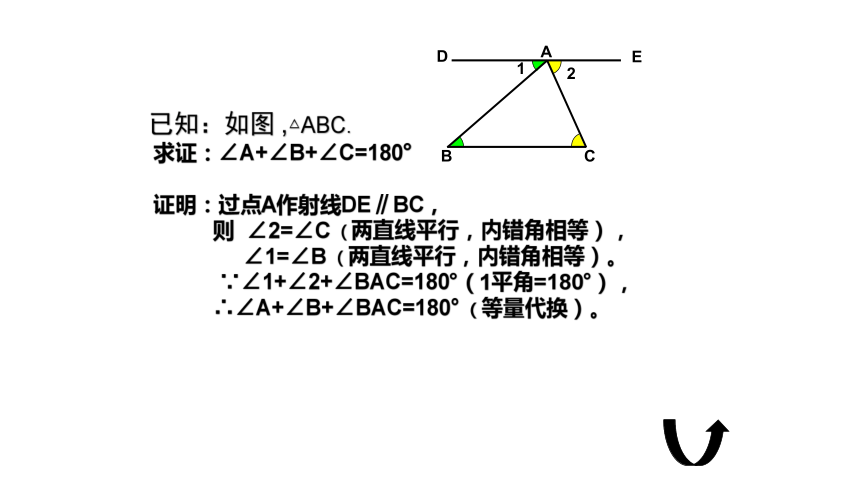
已知:如图 ,△ABC.
求证:∠A+∠B+∠C=180°
证明:过点A作射线DE∥BC,
则 ∠2=∠C (两直线平行,内错角相等),
∠1=∠B (两直线平行,内错角相等)。
∵∠1+∠2+∠BAC=180°(1平角=180°),
∴∠A+∠B+∠BAC=180° (等量代换)。
2
1
A
B
C
D
E
②这个点在三角形的边上如何?
C
2
1
A
B
3
E
F
D
已知:△ABC
求证:∠A+∠B+∠C=180?
证明:在△ABC边上任取一点D,过点D做直线DF∥AB, DE∥AC;
∵AB∥DF (已知)
∴∠B=∠1 (两直线平行,同位角相等)
∴∠A=∠DFC (两直线平行,同位角相等)
∵DE∥AC(已知)
∴∠C=∠2 (两直线平行,同位角相等)
∴∠DFC=∠3 (两直线平行,内错角相等)
∴∠A=∠3 (等量代换)
∵∠1+∠2+∠3=180?(平角定义)
∴∠A+∠B+∠C=180?
C
2
1
A
B
3
E
F
D
③这个点能否为三角形内部任意一点。
C
2
4
A
B
3
E
Q
D
F
P
G
H
1
已知:△ABC 求证:∠A+∠B+∠C=180?
证明:在△ABC内部任取一点D,过点D做直线EF∥BC, GQ∥AB;
PH∥AC;
∵EF∥BC (已知)
∴∠B=∠1 (两直线平行,同位角相等)
∴∠C=∠3 (两直线平行,同位角相等)
∵QG∥AB(已知)
∴∠1=∠2 (两直线平行,同位角相等)
∴∠A=∠DQF (两直线平行,同位角相等)
∵PH∥AC(已知)
∴∠PDQ=∠DQF (两直线平行,内错角相等)
∴∠3=∠4 (两直线平行,同位角相等)
∵∠B=∠1 ∠1=∠2 ∴∠B=∠2(等量代换)
∵∠C=∠3 ∠3=∠4 ∴∠C=∠4(等量代换)
∵∠A=∠DQF ∠PDQ=∠DQF ∴∠A=∠PDQ(等量代换)
∵∠2+∠4+∠PDQ=180?(平角定义)
∴∠A+∠B+∠C=180?
C
2
4
A
B
3
E
Q
D
F
P
G
H
1
④如果这个点运动到三角形的外部呢?
P
B
G
C
2
4
A
3
E
D
F
H
1
已知:△ABC 求证:∠A+∠B+∠C=180?
证明:在△ABC外部任取一点D,过点D做直线DE∥BC, DG∥AB;
DE∥BC;
∵EF∥BC (已知)
∴∠B=∠1 (两直线平行,同位角相等)
∴∠C=∠3 (两直线平行,同位角相等)
∵DG∥AB(已知)
∴∠1=∠2 (两直线平行,同位角相等)
∴∠A=∠AFD (两直线平行,内错角相等)
∵DH∥AC(已知)
∴∠3=∠4 (两直线平行,同位角相等)
∴∠AFD=∠HDP (两直线平行,同位角相等)
∵∠B=∠1 ∠1=∠2 ∴∠B=∠2(等量代换)
∵∠C=∠3 ∠3=∠4 ∴∠C=∠4(等量代换)
∵∠A=∠AFD ∠AFD=∠HDP ∴∠A=∠HDP(等量代换)
∵∠2+∠4+∠HDP=180?(平角定义)
∴∠A+∠B+∠C=180?
B
G
C
2
4
A
3
E
D
F
H
1
P
三角形三个内角的和等于180?
三角形内角和定理:
(2)基础知识巩固训练
1、 求出下列图形中x的值:(教材P16)
39?
108?
x?
x?
x?
x?
72?
x?
(x?-36?)
x?+36?
x?
x?
2. (1)如果三角形的三个内角的度数比是2:3:4,则它是( )
A、锐角三角形 B、钝角三角形
C、直角三角形 D、钝角或直角三角形
A
(2)在△ABC中,
A、30° B、60°
C、90° D、120°
C
3、在 △ABC中,∠B=∠A+10°,∠C=∠B+10°。求△ABC各内角的度数
解:∵∠B=∠A+10°,∠C=∠B+10°(已知)
∴∠C=∠A+10°+10°=∠A+20°
∵∠ A+∠B+∠C=180°
∴∠A+(∠A+10°)+(∠A+20°)=180°
∴∠A=50°,∠B=60°,∠C=70°
4、一个直角三角形最多有几个直角?
一个三角形最多有几个钝角?
至少有几个锐角?
请证明你的结论。
一个直角三角形最多有一个直角,一个三角形最多有一个钝角,至少有两个锐角。
5. 已知:在△ABC中, ∠BAC=40°, ∠B=75°,AD是△ABC的角平分线,求∠ADB的度数。
C
B
A
D
C
解:
6. 如图,C 岛在 A 岛的北偏东50°方向,B 岛在 A 岛的北偏东80 °方向,C 岛在 B 岛的北偏西40 °方向。从 C 岛看 A、B 两岛的视角∠ACB是多少度?
北
东
西
南
F
.
A
D
.
C
B
.
E
50°
80°
40°
北
东
西
南
北
东
西
南
(图中AD∥BE)
30°
H
A
.
C
.
D
50°
80°
北
东
西
南
30°
B
.
E
40°
北
东
西
南
F
A
.
C
.
D
50°
北
东
西
南
B
.
E
40°
北
东
西
南
A
.
C
.
D
50°
北
东
西
南
B
.
E
40°
北
东
西
南
H
A
.
C
.
D
50°
北
东
西
南
B
.
E
40°
北
东
西
南
(3)能力提高训练
1. 在△ABC中,如果∠A=∠B-∠C,那么这个三角形是( )
A . 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等边三角形
2. 锐角三角形任意两个内角的和必大于( )
A . 90 ° B. 100 ° C. 110 ° D. 120°
拓展:三角形和锐角三角形最大的角的取值范围分别是?
3. 如图,△ABC中,∠B=∠ACB,CD是高,求证 2∠BCD=∠A
A
B
C
D
B
A
证明: 在△ABC中, ∠A=180°-(∠B+∠ACB)
∵ ∠B=∠ACB
∴ ∠A=180°- 2∠B=2(90°-∠B)
在Rt △ BCD中, ∠BCD=90°-∠B.
∴ 2∠BCD=∠A
[60 °, 180°) [60 °, 90°)
4. 如图,在△ABC中,AD⊥BC,垂足为D,AE是 ∠BAC的平分线,交BC于E( ∠B> ∠C)。
(1)若∠C=45 °,∠B=65 °,求∠DAE的度数;
(2)试写出∠DAE与∠B和∠C之间的关系式。
A
B
C
D
E
解:⑴∵∠C=45 °, ∠B=65 °,
∴ ∠BAC=70 °
AE是∠BAC的平分线,∴ ∠BAE=35°
∴ ∠AED=180°-65°-35° =80 °
∵ AD⊥BC ∴ ∠ADE=90 °,∠DAE=10 °
⑵∠DAE= (∠B - ∠C)
谢谢各位光临
欢迎大家指导
三角形的内角和
同学们,你们知道“三角形
内角和等于180度”这个结论
最早是谁提出的吗?
数学史话
帕斯卡:(1623—1662)法国著名的数学家
方法:度量、剪拼、折叠
问题1 在小学我们已经知道任意一个三角形三个内角的和等于180°,你还记得是怎么发现这个结论的吗?请大家利用手中的三角形纸片进行探究.
实验操作,探究新知
B
A
C
任意画一个三角形,测量三角形的三个内角并求和,你有什么发现?
三角形三个内角的和是180?
1
2
B
A
C
已知:如图 ,△ABC.
求证:∠A+∠B+∠C=180°
证明:作BC的延长线CD,
过点C作射线CE∥BA,
则 ∠2=∠A (两直线平行,内错角相等),
∠1=∠B (两直线平行,同位角相等)。
∵∠1+∠2+∠ACB=180°(1平角=180°),
∴∠A+∠B+∠ACB=180° (等量代换)。
B
A
C
1
2
D
E
①过三角形一个顶点,用构造平角将三个角化归为平角来证明定理
那这个点是任意的吗?请同学们思考然后分小组讨论。
(1)思维能力训练
2
1
A
B
C
D
E
三角形的边上
三角形内部
三角形外部
归纳结论
已知:如图 ,△ABC.
求证:∠A+∠B+∠C=180°
证明:过点A作射线DE∥BC,
则 ∠2=∠C (两直线平行,内错角相等),
∠1=∠B (两直线平行,内错角相等)。
∵∠1+∠2+∠BAC=180°(1平角=180°),
∴∠A+∠B+∠BAC=180° (等量代换)。
2
1
A
B
C
D
E
②这个点在三角形的边上如何?
C
2
1
A
B
3
E
F
D
已知:△ABC
求证:∠A+∠B+∠C=180?
证明:在△ABC边上任取一点D,过点D做直线DF∥AB, DE∥AC;
∵AB∥DF (已知)
∴∠B=∠1 (两直线平行,同位角相等)
∴∠A=∠DFC (两直线平行,同位角相等)
∵DE∥AC(已知)
∴∠C=∠2 (两直线平行,同位角相等)
∴∠DFC=∠3 (两直线平行,内错角相等)
∴∠A=∠3 (等量代换)
∵∠1+∠2+∠3=180?(平角定义)
∴∠A+∠B+∠C=180?
C
2
1
A
B
3
E
F
D
③这个点能否为三角形内部任意一点。
C
2
4
A
B
3
E
Q
D
F
P
G
H
1
已知:△ABC 求证:∠A+∠B+∠C=180?
证明:在△ABC内部任取一点D,过点D做直线EF∥BC, GQ∥AB;
PH∥AC;
∵EF∥BC (已知)
∴∠B=∠1 (两直线平行,同位角相等)
∴∠C=∠3 (两直线平行,同位角相等)
∵QG∥AB(已知)
∴∠1=∠2 (两直线平行,同位角相等)
∴∠A=∠DQF (两直线平行,同位角相等)
∵PH∥AC(已知)
∴∠PDQ=∠DQF (两直线平行,内错角相等)
∴∠3=∠4 (两直线平行,同位角相等)
∵∠B=∠1 ∠1=∠2 ∴∠B=∠2(等量代换)
∵∠C=∠3 ∠3=∠4 ∴∠C=∠4(等量代换)
∵∠A=∠DQF ∠PDQ=∠DQF ∴∠A=∠PDQ(等量代换)
∵∠2+∠4+∠PDQ=180?(平角定义)
∴∠A+∠B+∠C=180?
C
2
4
A
B
3
E
Q
D
F
P
G
H
1
④如果这个点运动到三角形的外部呢?
P
B
G
C
2
4
A
3
E
D
F
H
1
已知:△ABC 求证:∠A+∠B+∠C=180?
证明:在△ABC外部任取一点D,过点D做直线DE∥BC, DG∥AB;
DE∥BC;
∵EF∥BC (已知)
∴∠B=∠1 (两直线平行,同位角相等)
∴∠C=∠3 (两直线平行,同位角相等)
∵DG∥AB(已知)
∴∠1=∠2 (两直线平行,同位角相等)
∴∠A=∠AFD (两直线平行,内错角相等)
∵DH∥AC(已知)
∴∠3=∠4 (两直线平行,同位角相等)
∴∠AFD=∠HDP (两直线平行,同位角相等)
∵∠B=∠1 ∠1=∠2 ∴∠B=∠2(等量代换)
∵∠C=∠3 ∠3=∠4 ∴∠C=∠4(等量代换)
∵∠A=∠AFD ∠AFD=∠HDP ∴∠A=∠HDP(等量代换)
∵∠2+∠4+∠HDP=180?(平角定义)
∴∠A+∠B+∠C=180?
B
G
C
2
4
A
3
E
D
F
H
1
P
三角形三个内角的和等于180?
三角形内角和定理:
(2)基础知识巩固训练
1、 求出下列图形中x的值:(教材P16)
39?
108?
x?
x?
x?
x?
72?
x?
(x?-36?)
x?+36?
x?
x?
2. (1)如果三角形的三个内角的度数比是2:3:4,则它是( )
A、锐角三角形 B、钝角三角形
C、直角三角形 D、钝角或直角三角形
A
(2)在△ABC中,
A、30° B、60°
C、90° D、120°
C
3、在 △ABC中,∠B=∠A+10°,∠C=∠B+10°。求△ABC各内角的度数
解:∵∠B=∠A+10°,∠C=∠B+10°(已知)
∴∠C=∠A+10°+10°=∠A+20°
∵∠ A+∠B+∠C=180°
∴∠A+(∠A+10°)+(∠A+20°)=180°
∴∠A=50°,∠B=60°,∠C=70°
4、一个直角三角形最多有几个直角?
一个三角形最多有几个钝角?
至少有几个锐角?
请证明你的结论。
一个直角三角形最多有一个直角,一个三角形最多有一个钝角,至少有两个锐角。
5. 已知:在△ABC中, ∠BAC=40°, ∠B=75°,AD是△ABC的角平分线,求∠ADB的度数。
C
B
A
D
C
解:
6. 如图,C 岛在 A 岛的北偏东50°方向,B 岛在 A 岛的北偏东80 °方向,C 岛在 B 岛的北偏西40 °方向。从 C 岛看 A、B 两岛的视角∠ACB是多少度?
北
东
西
南
F
.
A
D
.
C
B
.
E
50°
80°
40°
北
东
西
南
北
东
西
南
(图中AD∥BE)
30°
H
A
.
C
.
D
50°
80°
北
东
西
南
30°
B
.
E
40°
北
东
西
南
F
A
.
C
.
D
50°
北
东
西
南
B
.
E
40°
北
东
西
南
A
.
C
.
D
50°
北
东
西
南
B
.
E
40°
北
东
西
南
H
A
.
C
.
D
50°
北
东
西
南
B
.
E
40°
北
东
西
南
(3)能力提高训练
1. 在△ABC中,如果∠A=∠B-∠C,那么这个三角形是( )
A . 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等边三角形
2. 锐角三角形任意两个内角的和必大于( )
A . 90 ° B. 100 ° C. 110 ° D. 120°
拓展:三角形和锐角三角形最大的角的取值范围分别是?
3. 如图,△ABC中,∠B=∠ACB,CD是高,求证 2∠BCD=∠A
A
B
C
D
B
A
证明: 在△ABC中, ∠A=180°-(∠B+∠ACB)
∵ ∠B=∠ACB
∴ ∠A=180°- 2∠B=2(90°-∠B)
在Rt △ BCD中, ∠BCD=90°-∠B.
∴ 2∠BCD=∠A
[60 °, 180°) [60 °, 90°)
4. 如图,在△ABC中,AD⊥BC,垂足为D,AE是 ∠BAC的平分线,交BC于E( ∠B> ∠C)。
(1)若∠C=45 °,∠B=65 °,求∠DAE的度数;
(2)试写出∠DAE与∠B和∠C之间的关系式。
A
B
C
D
E
解:⑴∵∠C=45 °, ∠B=65 °,
∴ ∠BAC=70 °
AE是∠BAC的平分线,∴ ∠BAE=35°
∴ ∠AED=180°-65°-35° =80 °
∵ AD⊥BC ∴ ∠ADE=90 °,∠DAE=10 °
⑵∠DAE= (∠B - ∠C)
谢谢各位光临
欢迎大家指导
