人教A版高中数学必修2第二章 点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系课件(共68张PPT)
文档属性
| 名称 | 人教A版高中数学必修2第二章 点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系课件(共68张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 00:00:00 | ||
图片预览









文档简介
(共68张PPT)
空间点、直线、平面之间的位置关系
长方体的面给我们以平面的印象;生活中常见的如黑板、平整的操场、桌面、平静的湖面等等,都给我们以平面的印象。
实物引入、揭示课题
观察活动室里的地面,它呈现出怎样的形象?
实例引入
观察
1、平面的含义
以上实物都给我们以平面的印象,几何里所说的平面,就是从这样的一些物体中抽象出来的。平面是没有厚薄的,可以无限延伸,这是平面最基本的属性。
常见的桌面,黑板面,平静的水面等都是平面的局部形象;一个平面把空间分成两部分,一条直线把平面分成两部分
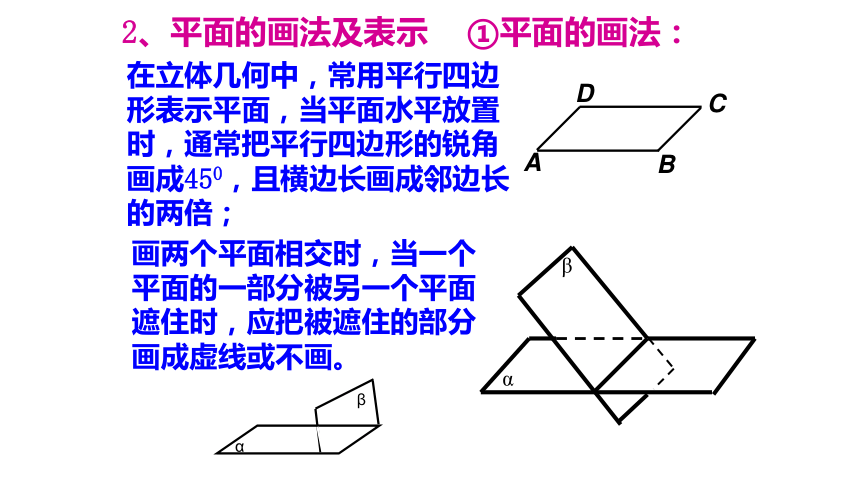
2、平面的画法及表示
①平面的画法:
在立体几何中,常用平行四边形表示平面,当平面水平放置时,通常把平行四边形的锐角画成450,且横边长画成邻边长的两倍;
D
C
A
B
画两个平面相交时,当一个平面的一部分被另一个平面遮住时,应把被遮住的部分画成虚线或不画。
α
β
α
β
②、平面的表示方法
D
C
A
B
平面ABCD
平面AC或平面BD
A
D
C
B
E
F
平面
记作:
平面
记作:
平面
常把希腊字母α、β、γ等写在代表平面的平行四边形的一个角上,如平面α、平面β等;也可以用代表平面的四边形的四个顶点,或者相对的两个顶点的大写英文字母作为这个平面的名称.
3、点、直线与平面的关系
平面内有无数个点,平面可以看成点的集合.
A
B
α
点A在平面α内,记作A∈α
B
·
·
A
·
.
.
m
点B在平面α外,
记作B?α
直线l在平面α内表示为
l?α
直线l不在平面α内表示为 l?α
1、判断下列各题的说法正确与否,在正
确的说法的题号后打 ,否则打 :
1、一个平面长 4 米,宽 2 米; ( )
2、平面有边界; ( )
3、一个平面的面积是 25 cm 2; ( )
4、菱形的面积是可以计算的; ( )
5、一个平面可以把空间分成两部分. ( )
练习
思考
4、平面的基本性质
如果直线 l 与平面α有一个公共点,直线 l 是否在平面α内?如果直线 l 与
平面α有两个公共点呢?
实际生活中,我们有这样的经验:把一根直尺边缘上的任意两点放到桌面上,可以看到,直尺的整个边缘就落在了桌面上.
图形语言
符号语言
B
·
·
A
·
.
.
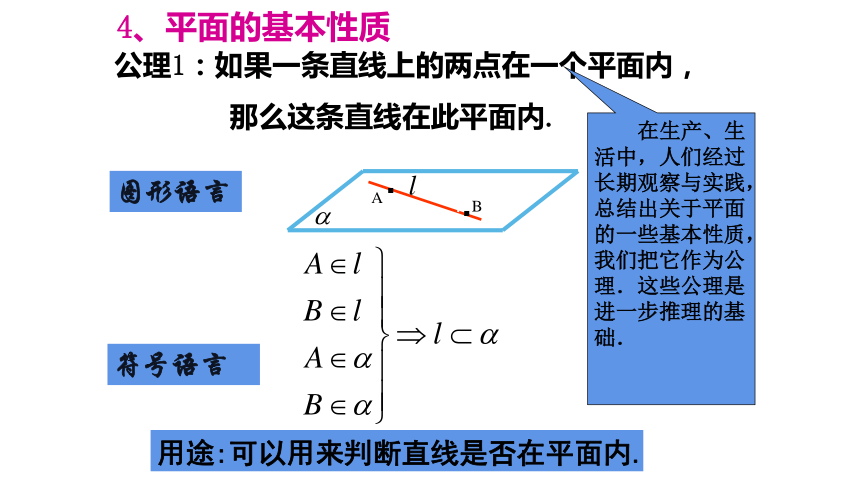
公理1:如果一条直线上的两点在一个平面内,
那么这条直线在此平面内.
用途:可以用来判断直线是否在平面内.
4、平面的基本性质
在生产、生活中,人们经过长期观察与实践,总结出关于平面的一些基本性质,我们把它作为公理.这些公理是进一步推理的基础.
生活中经常看到用三角架支撑照相机.或测量用的平板仪等等……
4、平面的基本性质
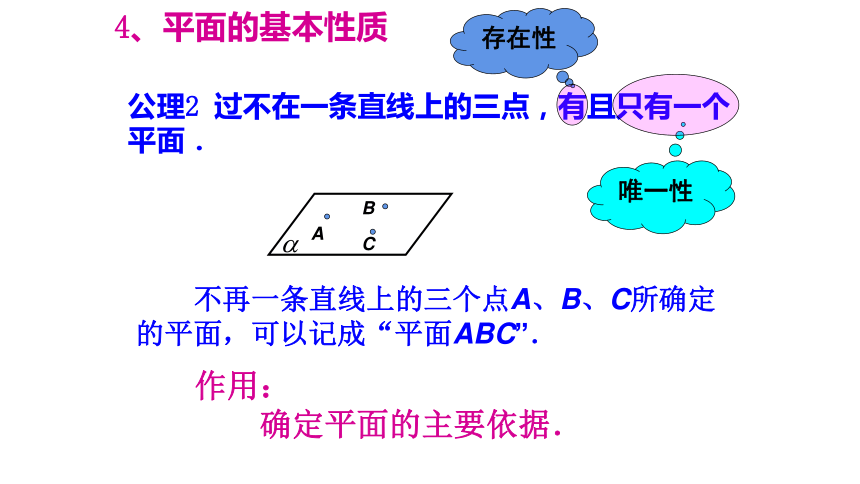
公理2 过不在一条直线上的三点,有且只有一个平面.
A
C
B
存在性
唯一性
作用:
确定平面的主要依据.
不再一条直线上的三个点A、B、C所确定的平面,可以记成“平面ABC”.
4、平面的基本性质
补充3个推论:
4、平面的基本性质
推论1:经过一条直线与直线外一点,有且只有一个平面。
推论2:经过两条平行直线,有且只有一个平面。
推论3:经过两条相交直线,有且只有一个平面。
B
把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B ?为什么?
思考
4、平面的基本性质
观察长方体,你能发现长方体的两个相交平面有没有公共直线吗?
观察
这条公共直线B’C’叫做这两个平面A’B’C’D’和平面BB’C’C的交线.
另一方面,相邻两个平面有一个公共点,如平面A’B’C’D’和平面BB’C’C有一个公共点B’,经过点B有且只有一条过该点的公共直线B’C’.
4、平面的基本性质
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
作用:
①判断两个平面相交的依据.
②判断点在直线上.
l
P
4、平面的基本性质
符号表示为:
图形表示为:
例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.
a
l
A
B
a
l
P
b
(1)
(2)
解:在(1)中,
在(2)中,
例题示范
课堂练习:课本P44?练习1、2、3、4
补练:
①有三个公共点的两个平面重合
②梯形的四个顶点在同一个平面内
③三条互相平行的直线必共面
④ 四条线段顺次首尾连接,构成平面图形
2、下列命题正确的是 ( )
A、两条直线可以确定一个平面
B、一条直线和一个点可以确定一个平面
C、空间不同的三点可以确定一个平面
D、两条相交直线可以确定一个平面
1、下列命题中,正确的命题是( )
A、圆上三点可以确定一个平面
B、圆心和圆上两点可确定一个平面
C、四条平行直线不能确定五个平面
D、空间四点中,若四点不共面,则任意三点不共线
4、若给定空间三条直线共面的条件,这四个条
件中不正确的是( )
①三条直线两两相交 ② 三条直线两两平行
③三条直线中有两条 ④平行三条直线共点
3、在空间中,下列命题错误的是( )
在正方体 中,判断下列命题是否正确,并说明理由:
①直线 在平面 内;
错误
随堂练习
在正方体 中,判断下列命题是否正确,并说明理由:
②设正方形ABCD与 的中心分别为O, ,则平面 与平面 的交线为 ;
正确
随堂练习
在正方体 中,判断下列命题是否正确,并说明理由:
③由点A,O,C可以确定一个平面;
错误
随堂练习
在正方体 中,判断下列命题是否正确,并说明理由:
④由 确定的平面是 ;
⑤由 确定的平面与由 确定的平面是同一个平面.
正确
正确
随堂练习
空间图形
文字叙述
符号表示
知识小结
实例引入平面
平面的画法和表示
点和平面的位置关系
平面三个公理
2.1.2空间中两直线的位置关系
判断下列命题对错:
1、如果一条直线上有一个点在一个平面上,则这条直线上的所有点都在这个平面内。( )
2、将书的一角接触课桌面,这时书所在平面和课桌所在平面只有一个公共点。 ( )
3、四个点中如果有三个点在同一条直线上,那么这四个点必在同一个平面内。 ( )
4、一条直线和一个点可以确定一个平面。( )
5、如果一条直线和另两条直线都相交,那么这三条直线可以确定一个平面。 ( )
平面有关知识(复习 )
?
?
?
?
?
判断下列直线的位置关系:
1、竖直的两条电线杆所在的直线
思考:在平面内,两条不重合的直线之间有几种位置关系?
2、十字路口的两条路所在的直线
3、教室内的日光灯管所在的直线与黑板的左右两侧
所在的直线
空间的两直线呢?
l
m
P
m
l
图1
图2
l
l
l
l
一、空间中两直线的位置关系
从图中可见,直线 l 与 m 既不相交,也不平行。空间中直线之间的这种关系称为异面直线。
不同在任何一个平面内的两条直线叫做异面直线。(既不相交也不平行的两条直线)
不同在任何一个平面内
1、异面直线
判断:
直线m和l是异面直线吗?
α
β
l
m
m
l
(1)
(2) ,则 与 是异面直线
(3)a,b不同在平面 内,则a与b异面
异面直线的画法:
通常用一个或两个平面来衬托,异面直线
不同在任何一个平面的特点
1、相交
2、平行
m
l
只有一个公共点
没有公共点
在同一平面
2、空间中两直线的三种位置关系
3、异面直线
m
P
l
没有公共点
不同在任一平面
m
l
P
探究:
H
G
C
A
D
B
E
F
G
H
E
F(B)
(C)
D
A
AB,CD,EF,GH这四条线段所在的直线是异面直线的有几对?相交直线有几对?平行直线有几对?
二、空间直线的平行关系
若a∥b,b∥c,
1、平行关系的传递性
c
a
a
b
c
c
公理4 平行于同一直线的两直线互相平行
a
α
则a∥c
例1:在正方体ABCD—A1B1C1D1中,直线 AB与C1D1 ,AD1与 BC1 是什么位置关系?为什么?
C1
A
B
C
D
A1
B1
D1
练习:在上例中,AA1与CC1,AC与A1C1
的位置是什么关系?
例题示范
例1: 在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
求证:四边形EFGH是平行四边形。
分析:
欲证EFGH是一个平行四边形
只需证EH∥FG且EH=FG
E,F,G,H分别是各边中点
连结BD,只需证:
EH ∥BD且EH = BD
FG ∥BD且FG = BD
A
B
D
E
F
G
H
C
例题示范
例1: 在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
求证:四边形EFGH是平行四边形。
A
B
D
E
F
G
H
C
∵ EH是△ABD的中位线
∴EH ∥BD且EH = BD
同理,FG ∥BD且FG = BD
∴EH ∥FG且EH =FG
∴EFGH是一个平行四边形
证明:
连结BD
变式一:
在例2中,如果再加上条件AC=BD,那么四边形EFGH是什么图形?
E
H
F
G
A
B
C
D
分析:
在例题2的基础上我们只需要证明平行四边形的两条邻边相等。
菱形
变式二:
空间四面体A--BCD中,E,H分别是AB,AD的中点,F,G分别是CB,CD上的点,且 ,
求证:四边形ABCD为梯形.
A
B
C
D
E
H
F
G
分析:需要证明四边形ABCD有
一组对边平行,但不相等。
3.?等角定理
定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
3.?等角定理
定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
定理的推论:如果两条相交直线和另两条相交直线分别平行,那么这两条直线所成的锐角(或直角)相等.
两直线的夹角:
两直线相交所成的4个角中,其中不大于
的角叫做两直线的夹角
三、两条异面直线所成的角
如图所示,a,b是两条异面直线,
在空间中任选一点O,
过O点分别作 a,b的平行线 a′和 b′,
a
b
P
a′
b′
O
则这两条线所成
的锐角θ(或直角),
θ
称为异面直线a,b所成的角。
?
任选
O
a′
若两条异面直线所成角为90°,则称它们互相垂直。
异面直线a与b垂直也记作a⊥b
异面直线所成角θ的取值范围:
平移
例 3 在正方体ABCD—A1B1C1D1中指出下列各对线段所成的角:
练习:1、求直线AD1与B1C所成的夹角;
2、与直线BB1垂直的棱有多少条?
1)AB与CC1;
2)A1 B1与AC;
3)A1B与D1B1。
B1
C
C1
A
B
D
A1
D1
1)AB与CC1所成的角
= 9 0°
2)A1 B1与AC所成的角
= 4 5°
3)A1B与D1B1所成的角
= 6 0°
2)与棱BB1垂直的棱有:
A
B
C
D
A1
B1
C1
D1
AD、
A1D1、
DC、
D1C1、
A1B1、
AB、
B1C1、
BC、
相交:
异面:
垂直
相交垂直
异面垂直
B1
C
C1
A
B
D
A1
D1
1)直线AD1与B1C所成的夹角
9 0°
例题示范
例2、如图,已知正方体ABCD-A'B'C'D'?中。
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'?和CC'?的夹角是多少?
(3)哪些棱所在的直线与直线AA'?垂直?
解:(1)由异面直线的判定方法可知,与直线
成异面直线的有直线
,
例题示范
例2、如图,已知正方体ABCD-A'B'C'D'?中。
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'?和CC'?的夹角是多少?
(3)哪些棱所在的直线与直线AA'?垂直?
解:(2)由 可知,
等于异面直线 与
的夹角,所以异面直线
与 的夹角为450 。
(3) 直线
与直线 都垂直.
填空:
1、空间两条不重合的直线的位置关系有________、 ________、 ________三种。
2、没有公共点的两条直线可能是________直线,也有可能是
________直线。
3、和两条异面直线中的一条平行的直线与另一条的位置关系
有______________。
4 、过已知直线上一点可以作______条直线与已知直线垂直。
5 、过已知直线外一点可以作______条直线与已知直线垂直。
平行
相交
异面
平行
异面
无数
无数
相交、异面
1、分别在两个平面内的两条直线一定是异面直线。( )
2、空间两条不相交的直线一定是异面直线。 ( )
3、垂直于同一条直线的两条直线必平行。 ( )
4、若一条直线垂直于两条平行直线中的一条,则它一定与另一条直线垂直。 ( )
?
?
?
?
判断对错:
练习反馈:
1. 判断:
(1)平行于同一直线的两条直线平行.( )
(2)垂直于同一直线的两条直线平行.( ?)
(3)过直线外一点,有且只有一条直线与已知直线平行?.?( )
(4)与已知直线平行且距离等于定长的直线只有两条.????( )
(5)若一个角的两边分别与另一个角的两边平行,那么这两个角相等( )
(6)若两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.?(???)????
√
×
√
√
×
×
练习反馈:
2.选择题
?(1)“a,b是异面直线”是指?①?a∩b=Φ,且a不平行于b;②?a ?平面a,b?平面b且a∩b=Φ ③?a??平面a,b??平面a?④?不存在平面a,能使a??a且b??a成立
上述结论中,正确的是 (???)
(A)①② (B)①③ (C)①④ (D)③④
(2)长方体的一条对角线与长方体的棱所组成的异面直线有 (???)
?(A)2对 (B)3对 (C)6对 (D)12对
C
C
(3)两条直线a,b分别和异面直线c,d都相交,则直线a,b的位置关系是(??)
?(A)一定是异面直线 (B)一定是相交直线
?(C)可能是平行直线
(D)可能是异面直线,也可能是相交直线
(4)一条直线和两条异面直线中的一条平行,则它和另一条的位置关系是(? )
(A)平行 (B)相交
(C)异面 (D)相交或异面
3.两条直线互相垂直,它们一定相交吗????
答:不一定,还可能异面.
D
D
4.垂直于同一直线的两条直线,有几种位置关系?
答:三种:相交,平行,异面.
5.画两个相交平面,在这两个平面内各画一条直线使它们成为(1)平行直线;(2)相交直线;(3)异面直线.
6.选择题
?(1)分别在两个平面内的两条直线间的位置关系是 (? )
?(A)异面 (B)平行
(C)相交 (D)以上都有可能??
(2)异面直线a,b满足a??a,b??b,a∩b=l,
则l与a,b的位置关系一定是(? )
(A)l至多与a,b中的一条相交;
(B)l至少与a,b中的一条相交;
(C)l与a,b都相交;
(D)l至少与a,b中的一条平行.
D
B
(3)两异面直线所成的角的范围是 ( )
(A)(0°,90°) (B)[0°,90°)
(C)(0°,90°] (D)[0°,90°]
7.判断下列命题的真假,真的打“√”,假的打“×”
?(1)两条直线和第三条直线成等角,则这两条直线平行???????????(???)
?(2)平行移动两条异面直线中的任一条,它们所成的角不变???????(??)
?(3)四边相等且四个角也相等的四边形是正方形?????????????????(???)
C
×
√
×
课堂小结:
这节课我们学习了两条直线的位置关系(平行、相交、异面),平行公理和等角定理及其推论.异面直线的概念、判断及异面直线夹角的概念;
证明两直线异面的一般方法是“反证法”或“判定定理”;求异面直线的夹角的一般步骤是:“作—证—算—答”?
?
作业布置:
P51 A组3、4(1)(2)(3)、5、6.
2.1.3《空间中直线与
平面之间的位置关系》
复习引入:
1、空间两直线的位置关系
(1)相交;(2)平行;(3)异面
2.公理4的内容是什么?
平行于同一条直线的两条直线互相平行.
3.等角定理的内容是什么?
空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
4.等角定理的推论是什么?
如果两条相交直线和另两条相交直线分别平行,那么这两条直线所成的锐角(或直角)相等.
5.什么是异面直线?什么是异面直线所成的角?
什么是异面直线垂直?异面直线定理的内容是什么?
研探新知
(1)一支笔所在直线与一个作业本所在的平面,可能有几种位置关系?
A1
B1
C1
D1
A
B
C
D
(2)如图,线段A1B所在直线与长方体ABCD-A1B1C1D1的六个面所在平面有几种位置关系?
α
a
直线与平面α相交
α
A
a
a
α
直线与平面α平行
a∥α
无交点
直线在平面α内
有无数个交点
a?α
a ∩ α= A
有且只有一个交点
结论:
直线与平面的位置关系有且只有三种:
例1、下列命题中正确的个数是( )
①若直线 上有无数个点不在平面α内,则
②若直线 与平面α平行,则 与平面α内的任意一条直线平行
③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行
④若直线 与平面α平行,则 与平面α内的任意一条直线都没有公共点.
(A)0 (B) 1
(C)2 (D) 3
例题示范:
分析:可以借助长方体模型来看上述问题是否正确。
问题(1)不正确,相交时也符合。
问题(2)不正确,
如右图中,A'B与
平面DCC'D’平行,
但它与CD不平行。
问题(3)不正确。
另一条直线有可能在平面内,如AB∥CD,AB与平面DCC'D’平行,但直线CD?平面DCC'D’
问题(4)正确,所以选(B)。
例题示范:
例2?已知直线a在平面α外,则 (???)
(A)a∥α??? ?(B)直线a与平面α至少有一个公共点 (C)a?α=A
(D)直线a与平面α至多有一个公共点。
例题示范:
D
巩固练习:?
1.选择题
(1)以下命题(其中a,b表示直线,a表示平面)
①若a∥b,b?a,则a∥a???②若a∥a,b∥a,则a∥b ③若a∥b,b∥a,则a∥a???④若a∥a,b?a,则a∥b 其中正确命题的个数是 ( )
(A)0个 (B)1个 (C)2个 (D)3个
A
2.已知a∥a,b∥a,则直线a,b的位置关系
①平行;②垂直不相交;③垂直相交;
④相交;⑤不垂直且不相交.??
其中可能成立的有 (???)
(A)2个 (B)3个 (C)4个 (D)5个
3.如果平面a外有两点A、B,它们到平面a的距离都是a,则直线AB和平面a的位置关系一定是(???)
(A)平行 (B)相交???
(C)平行或相交??(D)AB ?a
巩固练习:?
D
C
巩固练习:?
4.已知m,n为异面直线,m∥平面a,n∥平面b,a∩b=l,则l (???)
(A)与m,n都相交??????
(B)与m,n中至少一条相交
(C)与m,n都不相交???
(D)与m,n中一条相交
C
5.完成教材P49?练习?
2.1.4空间两个平面之间的位置关系
(一)两个平面的位置关系:
1. 观察实例;
2. 两个平面的位置关系:
(1) 两个平面平行——没有公共点;
(2) 两个平面相交——有一条公共直线;
3. 两个平面平行的画法:
(2)不正确画法
O
4. 两个平面相交的画法:
空间点、直线、平面之间的位置关系
长方体的面给我们以平面的印象;生活中常见的如黑板、平整的操场、桌面、平静的湖面等等,都给我们以平面的印象。
实物引入、揭示课题
观察活动室里的地面,它呈现出怎样的形象?
实例引入
观察
1、平面的含义
以上实物都给我们以平面的印象,几何里所说的平面,就是从这样的一些物体中抽象出来的。平面是没有厚薄的,可以无限延伸,这是平面最基本的属性。
常见的桌面,黑板面,平静的水面等都是平面的局部形象;一个平面把空间分成两部分,一条直线把平面分成两部分
2、平面的画法及表示
①平面的画法:
在立体几何中,常用平行四边形表示平面,当平面水平放置时,通常把平行四边形的锐角画成450,且横边长画成邻边长的两倍;
D
C
A
B
画两个平面相交时,当一个平面的一部分被另一个平面遮住时,应把被遮住的部分画成虚线或不画。
α
β
α
β
②、平面的表示方法
D
C
A
B
平面ABCD
平面AC或平面BD
A
D
C
B
E
F
平面
记作:
平面
记作:
平面
常把希腊字母α、β、γ等写在代表平面的平行四边形的一个角上,如平面α、平面β等;也可以用代表平面的四边形的四个顶点,或者相对的两个顶点的大写英文字母作为这个平面的名称.
3、点、直线与平面的关系
平面内有无数个点,平面可以看成点的集合.
A
B
α
点A在平面α内,记作A∈α
B
·
·
A
·
.
.
m
点B在平面α外,
记作B?α
直线l在平面α内表示为
l?α
直线l不在平面α内表示为 l?α
1、判断下列各题的说法正确与否,在正
确的说法的题号后打 ,否则打 :
1、一个平面长 4 米,宽 2 米; ( )
2、平面有边界; ( )
3、一个平面的面积是 25 cm 2; ( )
4、菱形的面积是可以计算的; ( )
5、一个平面可以把空间分成两部分. ( )
练习
思考
4、平面的基本性质
如果直线 l 与平面α有一个公共点,直线 l 是否在平面α内?如果直线 l 与
平面α有两个公共点呢?
实际生活中,我们有这样的经验:把一根直尺边缘上的任意两点放到桌面上,可以看到,直尺的整个边缘就落在了桌面上.
图形语言
符号语言
B
·
·
A
·
.
.
公理1:如果一条直线上的两点在一个平面内,
那么这条直线在此平面内.
用途:可以用来判断直线是否在平面内.
4、平面的基本性质
在生产、生活中,人们经过长期观察与实践,总结出关于平面的一些基本性质,我们把它作为公理.这些公理是进一步推理的基础.
生活中经常看到用三角架支撑照相机.或测量用的平板仪等等……
4、平面的基本性质
公理2 过不在一条直线上的三点,有且只有一个平面.
A
C
B
存在性
唯一性
作用:
确定平面的主要依据.
不再一条直线上的三个点A、B、C所确定的平面,可以记成“平面ABC”.
4、平面的基本性质
补充3个推论:
4、平面的基本性质
推论1:经过一条直线与直线外一点,有且只有一个平面。
推论2:经过两条平行直线,有且只有一个平面。
推论3:经过两条相交直线,有且只有一个平面。
B
把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B ?为什么?
思考
4、平面的基本性质
观察长方体,你能发现长方体的两个相交平面有没有公共直线吗?
观察
这条公共直线B’C’叫做这两个平面A’B’C’D’和平面BB’C’C的交线.
另一方面,相邻两个平面有一个公共点,如平面A’B’C’D’和平面BB’C’C有一个公共点B’,经过点B有且只有一条过该点的公共直线B’C’.
4、平面的基本性质
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
作用:
①判断两个平面相交的依据.
②判断点在直线上.
l
P
4、平面的基本性质
符号表示为:
图形表示为:
例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.
a
l
A
B
a
l
P
b
(1)
(2)
解:在(1)中,
在(2)中,
例题示范
课堂练习:课本P44?练习1、2、3、4
补练:
①有三个公共点的两个平面重合
②梯形的四个顶点在同一个平面内
③三条互相平行的直线必共面
④ 四条线段顺次首尾连接,构成平面图形
2、下列命题正确的是 ( )
A、两条直线可以确定一个平面
B、一条直线和一个点可以确定一个平面
C、空间不同的三点可以确定一个平面
D、两条相交直线可以确定一个平面
1、下列命题中,正确的命题是( )
A、圆上三点可以确定一个平面
B、圆心和圆上两点可确定一个平面
C、四条平行直线不能确定五个平面
D、空间四点中,若四点不共面,则任意三点不共线
4、若给定空间三条直线共面的条件,这四个条
件中不正确的是( )
①三条直线两两相交 ② 三条直线两两平行
③三条直线中有两条 ④平行三条直线共点
3、在空间中,下列命题错误的是( )
在正方体 中,判断下列命题是否正确,并说明理由:
①直线 在平面 内;
错误
随堂练习
在正方体 中,判断下列命题是否正确,并说明理由:
②设正方形ABCD与 的中心分别为O, ,则平面 与平面 的交线为 ;
正确
随堂练习
在正方体 中,判断下列命题是否正确,并说明理由:
③由点A,O,C可以确定一个平面;
错误
随堂练习
在正方体 中,判断下列命题是否正确,并说明理由:
④由 确定的平面是 ;
⑤由 确定的平面与由 确定的平面是同一个平面.
正确
正确
随堂练习
空间图形
文字叙述
符号表示
知识小结
实例引入平面
平面的画法和表示
点和平面的位置关系
平面三个公理
2.1.2空间中两直线的位置关系
判断下列命题对错:
1、如果一条直线上有一个点在一个平面上,则这条直线上的所有点都在这个平面内。( )
2、将书的一角接触课桌面,这时书所在平面和课桌所在平面只有一个公共点。 ( )
3、四个点中如果有三个点在同一条直线上,那么这四个点必在同一个平面内。 ( )
4、一条直线和一个点可以确定一个平面。( )
5、如果一条直线和另两条直线都相交,那么这三条直线可以确定一个平面。 ( )
平面有关知识(复习 )
?
?
?
?
?
判断下列直线的位置关系:
1、竖直的两条电线杆所在的直线
思考:在平面内,两条不重合的直线之间有几种位置关系?
2、十字路口的两条路所在的直线
3、教室内的日光灯管所在的直线与黑板的左右两侧
所在的直线
空间的两直线呢?
l
m
P
m
l
图1
图2
l
l
l
l
一、空间中两直线的位置关系
从图中可见,直线 l 与 m 既不相交,也不平行。空间中直线之间的这种关系称为异面直线。
不同在任何一个平面内的两条直线叫做异面直线。(既不相交也不平行的两条直线)
不同在任何一个平面内
1、异面直线
判断:
直线m和l是异面直线吗?
α
β
l
m
m
l
(1)
(2) ,则 与 是异面直线
(3)a,b不同在平面 内,则a与b异面
异面直线的画法:
通常用一个或两个平面来衬托,异面直线
不同在任何一个平面的特点
1、相交
2、平行
m
l
只有一个公共点
没有公共点
在同一平面
2、空间中两直线的三种位置关系
3、异面直线
m
P
l
没有公共点
不同在任一平面
m
l
P
探究:
H
G
C
A
D
B
E
F
G
H
E
F(B)
(C)
D
A
AB,CD,EF,GH这四条线段所在的直线是异面直线的有几对?相交直线有几对?平行直线有几对?
二、空间直线的平行关系
若a∥b,b∥c,
1、平行关系的传递性
c
a
a
b
c
c
公理4 平行于同一直线的两直线互相平行
a
α
则a∥c
例1:在正方体ABCD—A1B1C1D1中,直线 AB与C1D1 ,AD1与 BC1 是什么位置关系?为什么?
C1
A
B
C
D
A1
B1
D1
练习:在上例中,AA1与CC1,AC与A1C1
的位置是什么关系?
例题示范
例1: 在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
求证:四边形EFGH是平行四边形。
分析:
欲证EFGH是一个平行四边形
只需证EH∥FG且EH=FG
E,F,G,H分别是各边中点
连结BD,只需证:
EH ∥BD且EH = BD
FG ∥BD且FG = BD
A
B
D
E
F
G
H
C
例题示范
例1: 在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
求证:四边形EFGH是平行四边形。
A
B
D
E
F
G
H
C
∵ EH是△ABD的中位线
∴EH ∥BD且EH = BD
同理,FG ∥BD且FG = BD
∴EH ∥FG且EH =FG
∴EFGH是一个平行四边形
证明:
连结BD
变式一:
在例2中,如果再加上条件AC=BD,那么四边形EFGH是什么图形?
E
H
F
G
A
B
C
D
分析:
在例题2的基础上我们只需要证明平行四边形的两条邻边相等。
菱形
变式二:
空间四面体A--BCD中,E,H分别是AB,AD的中点,F,G分别是CB,CD上的点,且 ,
求证:四边形ABCD为梯形.
A
B
C
D
E
H
F
G
分析:需要证明四边形ABCD有
一组对边平行,但不相等。
3.?等角定理
定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
3.?等角定理
定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
定理的推论:如果两条相交直线和另两条相交直线分别平行,那么这两条直线所成的锐角(或直角)相等.
两直线的夹角:
两直线相交所成的4个角中,其中不大于
的角叫做两直线的夹角
三、两条异面直线所成的角
如图所示,a,b是两条异面直线,
在空间中任选一点O,
过O点分别作 a,b的平行线 a′和 b′,
a
b
P
a′
b′
O
则这两条线所成
的锐角θ(或直角),
θ
称为异面直线a,b所成的角。
?
任选
O
a′
若两条异面直线所成角为90°,则称它们互相垂直。
异面直线a与b垂直也记作a⊥b
异面直线所成角θ的取值范围:
平移
例 3 在正方体ABCD—A1B1C1D1中指出下列各对线段所成的角:
练习:1、求直线AD1与B1C所成的夹角;
2、与直线BB1垂直的棱有多少条?
1)AB与CC1;
2)A1 B1与AC;
3)A1B与D1B1。
B1
C
C1
A
B
D
A1
D1
1)AB与CC1所成的角
= 9 0°
2)A1 B1与AC所成的角
= 4 5°
3)A1B与D1B1所成的角
= 6 0°
2)与棱BB1垂直的棱有:
A
B
C
D
A1
B1
C1
D1
AD、
A1D1、
DC、
D1C1、
A1B1、
AB、
B1C1、
BC、
相交:
异面:
垂直
相交垂直
异面垂直
B1
C
C1
A
B
D
A1
D1
1)直线AD1与B1C所成的夹角
9 0°
例题示范
例2、如图,已知正方体ABCD-A'B'C'D'?中。
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'?和CC'?的夹角是多少?
(3)哪些棱所在的直线与直线AA'?垂直?
解:(1)由异面直线的判定方法可知,与直线
成异面直线的有直线
,
例题示范
例2、如图,已知正方体ABCD-A'B'C'D'?中。
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'?和CC'?的夹角是多少?
(3)哪些棱所在的直线与直线AA'?垂直?
解:(2)由 可知,
等于异面直线 与
的夹角,所以异面直线
与 的夹角为450 。
(3) 直线
与直线 都垂直.
填空:
1、空间两条不重合的直线的位置关系有________、 ________、 ________三种。
2、没有公共点的两条直线可能是________直线,也有可能是
________直线。
3、和两条异面直线中的一条平行的直线与另一条的位置关系
有______________。
4 、过已知直线上一点可以作______条直线与已知直线垂直。
5 、过已知直线外一点可以作______条直线与已知直线垂直。
平行
相交
异面
平行
异面
无数
无数
相交、异面
1、分别在两个平面内的两条直线一定是异面直线。( )
2、空间两条不相交的直线一定是异面直线。 ( )
3、垂直于同一条直线的两条直线必平行。 ( )
4、若一条直线垂直于两条平行直线中的一条,则它一定与另一条直线垂直。 ( )
?
?
?
?
判断对错:
练习反馈:
1. 判断:
(1)平行于同一直线的两条直线平行.( )
(2)垂直于同一直线的两条直线平行.( ?)
(3)过直线外一点,有且只有一条直线与已知直线平行?.?( )
(4)与已知直线平行且距离等于定长的直线只有两条.????( )
(5)若一个角的两边分别与另一个角的两边平行,那么这两个角相等( )
(6)若两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.?(???)????
√
×
√
√
×
×
练习反馈:
2.选择题
?(1)“a,b是异面直线”是指?①?a∩b=Φ,且a不平行于b;②?a ?平面a,b?平面b且a∩b=Φ ③?a??平面a,b??平面a?④?不存在平面a,能使a??a且b??a成立
上述结论中,正确的是 (???)
(A)①② (B)①③ (C)①④ (D)③④
(2)长方体的一条对角线与长方体的棱所组成的异面直线有 (???)
?(A)2对 (B)3对 (C)6对 (D)12对
C
C
(3)两条直线a,b分别和异面直线c,d都相交,则直线a,b的位置关系是(??)
?(A)一定是异面直线 (B)一定是相交直线
?(C)可能是平行直线
(D)可能是异面直线,也可能是相交直线
(4)一条直线和两条异面直线中的一条平行,则它和另一条的位置关系是(? )
(A)平行 (B)相交
(C)异面 (D)相交或异面
3.两条直线互相垂直,它们一定相交吗????
答:不一定,还可能异面.
D
D
4.垂直于同一直线的两条直线,有几种位置关系?
答:三种:相交,平行,异面.
5.画两个相交平面,在这两个平面内各画一条直线使它们成为(1)平行直线;(2)相交直线;(3)异面直线.
6.选择题
?(1)分别在两个平面内的两条直线间的位置关系是 (? )
?(A)异面 (B)平行
(C)相交 (D)以上都有可能??
(2)异面直线a,b满足a??a,b??b,a∩b=l,
则l与a,b的位置关系一定是(? )
(A)l至多与a,b中的一条相交;
(B)l至少与a,b中的一条相交;
(C)l与a,b都相交;
(D)l至少与a,b中的一条平行.
D
B
(3)两异面直线所成的角的范围是 ( )
(A)(0°,90°) (B)[0°,90°)
(C)(0°,90°] (D)[0°,90°]
7.判断下列命题的真假,真的打“√”,假的打“×”
?(1)两条直线和第三条直线成等角,则这两条直线平行???????????(???)
?(2)平行移动两条异面直线中的任一条,它们所成的角不变???????(??)
?(3)四边相等且四个角也相等的四边形是正方形?????????????????(???)
C
×
√
×
课堂小结:
这节课我们学习了两条直线的位置关系(平行、相交、异面),平行公理和等角定理及其推论.异面直线的概念、判断及异面直线夹角的概念;
证明两直线异面的一般方法是“反证法”或“判定定理”;求异面直线的夹角的一般步骤是:“作—证—算—答”?
?
作业布置:
P51 A组3、4(1)(2)(3)、5、6.
2.1.3《空间中直线与
平面之间的位置关系》
复习引入:
1、空间两直线的位置关系
(1)相交;(2)平行;(3)异面
2.公理4的内容是什么?
平行于同一条直线的两条直线互相平行.
3.等角定理的内容是什么?
空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
4.等角定理的推论是什么?
如果两条相交直线和另两条相交直线分别平行,那么这两条直线所成的锐角(或直角)相等.
5.什么是异面直线?什么是异面直线所成的角?
什么是异面直线垂直?异面直线定理的内容是什么?
研探新知
(1)一支笔所在直线与一个作业本所在的平面,可能有几种位置关系?
A1
B1
C1
D1
A
B
C
D
(2)如图,线段A1B所在直线与长方体ABCD-A1B1C1D1的六个面所在平面有几种位置关系?
α
a
直线与平面α相交
α
A
a
a
α
直线与平面α平行
a∥α
无交点
直线在平面α内
有无数个交点
a?α
a ∩ α= A
有且只有一个交点
结论:
直线与平面的位置关系有且只有三种:
例1、下列命题中正确的个数是( )
①若直线 上有无数个点不在平面α内,则
②若直线 与平面α平行,则 与平面α内的任意一条直线平行
③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行
④若直线 与平面α平行,则 与平面α内的任意一条直线都没有公共点.
(A)0 (B) 1
(C)2 (D) 3
例题示范:
分析:可以借助长方体模型来看上述问题是否正确。
问题(1)不正确,相交时也符合。
问题(2)不正确,
如右图中,A'B与
平面DCC'D’平行,
但它与CD不平行。
问题(3)不正确。
另一条直线有可能在平面内,如AB∥CD,AB与平面DCC'D’平行,但直线CD?平面DCC'D’
问题(4)正确,所以选(B)。
例题示范:
例2?已知直线a在平面α外,则 (???)
(A)a∥α??? ?(B)直线a与平面α至少有一个公共点 (C)a?α=A
(D)直线a与平面α至多有一个公共点。
例题示范:
D
巩固练习:?
1.选择题
(1)以下命题(其中a,b表示直线,a表示平面)
①若a∥b,b?a,则a∥a???②若a∥a,b∥a,则a∥b ③若a∥b,b∥a,则a∥a???④若a∥a,b?a,则a∥b 其中正确命题的个数是 ( )
(A)0个 (B)1个 (C)2个 (D)3个
A
2.已知a∥a,b∥a,则直线a,b的位置关系
①平行;②垂直不相交;③垂直相交;
④相交;⑤不垂直且不相交.??
其中可能成立的有 (???)
(A)2个 (B)3个 (C)4个 (D)5个
3.如果平面a外有两点A、B,它们到平面a的距离都是a,则直线AB和平面a的位置关系一定是(???)
(A)平行 (B)相交???
(C)平行或相交??(D)AB ?a
巩固练习:?
D
C
巩固练习:?
4.已知m,n为异面直线,m∥平面a,n∥平面b,a∩b=l,则l (???)
(A)与m,n都相交??????
(B)与m,n中至少一条相交
(C)与m,n都不相交???
(D)与m,n中一条相交
C
5.完成教材P49?练习?
2.1.4空间两个平面之间的位置关系
(一)两个平面的位置关系:
1. 观察实例;
2. 两个平面的位置关系:
(1) 两个平面平行——没有公共点;
(2) 两个平面相交——有一条公共直线;
3. 两个平面平行的画法:
(2)不正确画法
O
4. 两个平面相交的画法:
