安徽省合肥市长丰县2020届九年级上学期期末质量检测数学试题(含答案)
文档属性
| 名称 | 安徽省合肥市长丰县2020届九年级上学期期末质量检测数学试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-11 19:55:23 | ||
图片预览


文档简介
长丰县2020年九年级期末质量检测数学试卷
一、选择题:本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 抛物线的顶点坐标是( )
A. B. C. D.
2. 在中,,,,则长是( )
A.4 B.6 C.8 D.10
3. 将抛物线向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的表达式是( )
A. B.
C. D.
4. 关于反比例函数,下列说法正确的是( )
A.图象过点 B.图象在第一、三象限
C.当时,随的增大而减小 D.当时,随的增大而增大
5. 已知抛物线()经过,,,四点,则与的大小关系是( )
A. B. C. D.不能确定
6. 如图,在中,为的中点,为的中点,的延长线交于点,则的值是( )
A.1:5 B.1:4 C.1:3 D.1:2
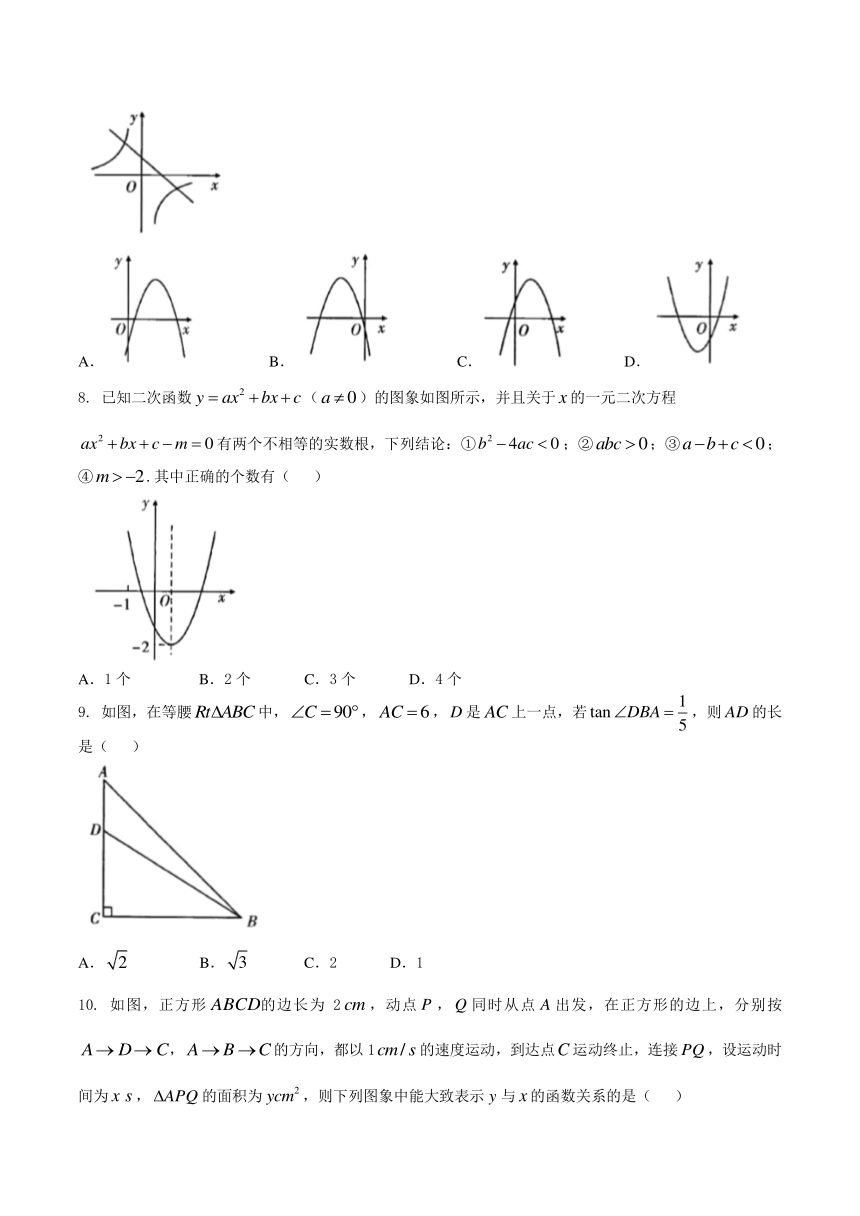
7. 一次函数和反比例函数在同一个平面直角坐标系中的图象如图所示,则二次函数的图象可能是( )
A. B. C. D.
8. 已知二次函数()的图象如图所示,并且关于的一元二次方程
有两个不相等的实数根,下列结论:①;②;③;④.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
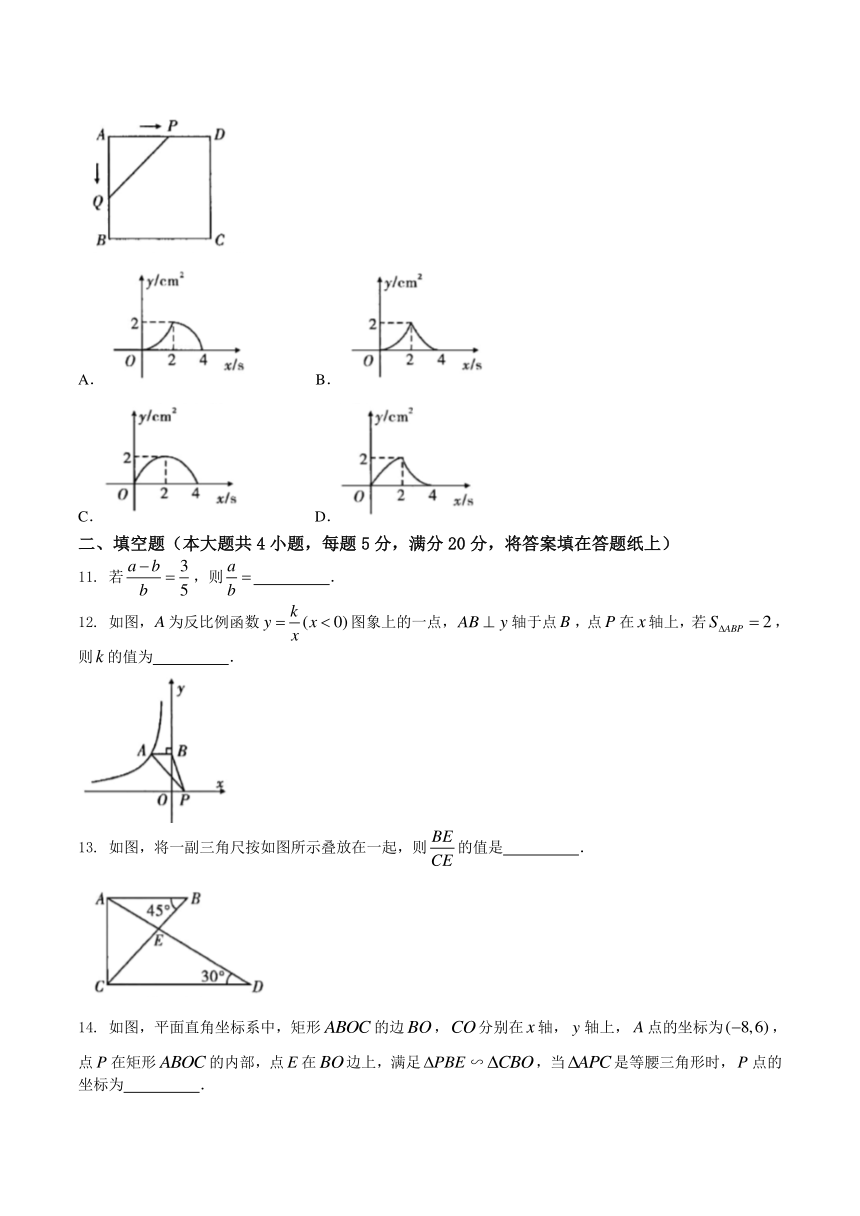
9. 如图,在等腰中,,,是上一点,若,则的长是( )
A. B. C.2 D.1
10. 如图,正方形的边长为2,动点,同时从点出发,在正方形的边上,分别按,的方向,都以1的速度运动,到达点运动终止,连接,设运动时间为,的面积为,则下列图象中能大致表示与的函数关系的是( )
A. B.
C. D.
二、填空题(本大题共4小题,每题5分,满分20分,将答案填在答题纸上)
11. 若,则 .
12. 如图,为反比例函数图象上的一点,轴于点,点在轴上,若,则的值为 .
13. 如图,将一副三角尺按如图所示叠放在一起,则的值是 .
14. 如图,平面直角坐标系中,矩形的边,分别在轴,轴上,点的坐标为,点在矩形的内部,点在边上,满足∽,当是等腰三角形时,点的坐标为 .
三、解答题:本大题共2小题,每小题8分,满分16分.
15. 计算:.
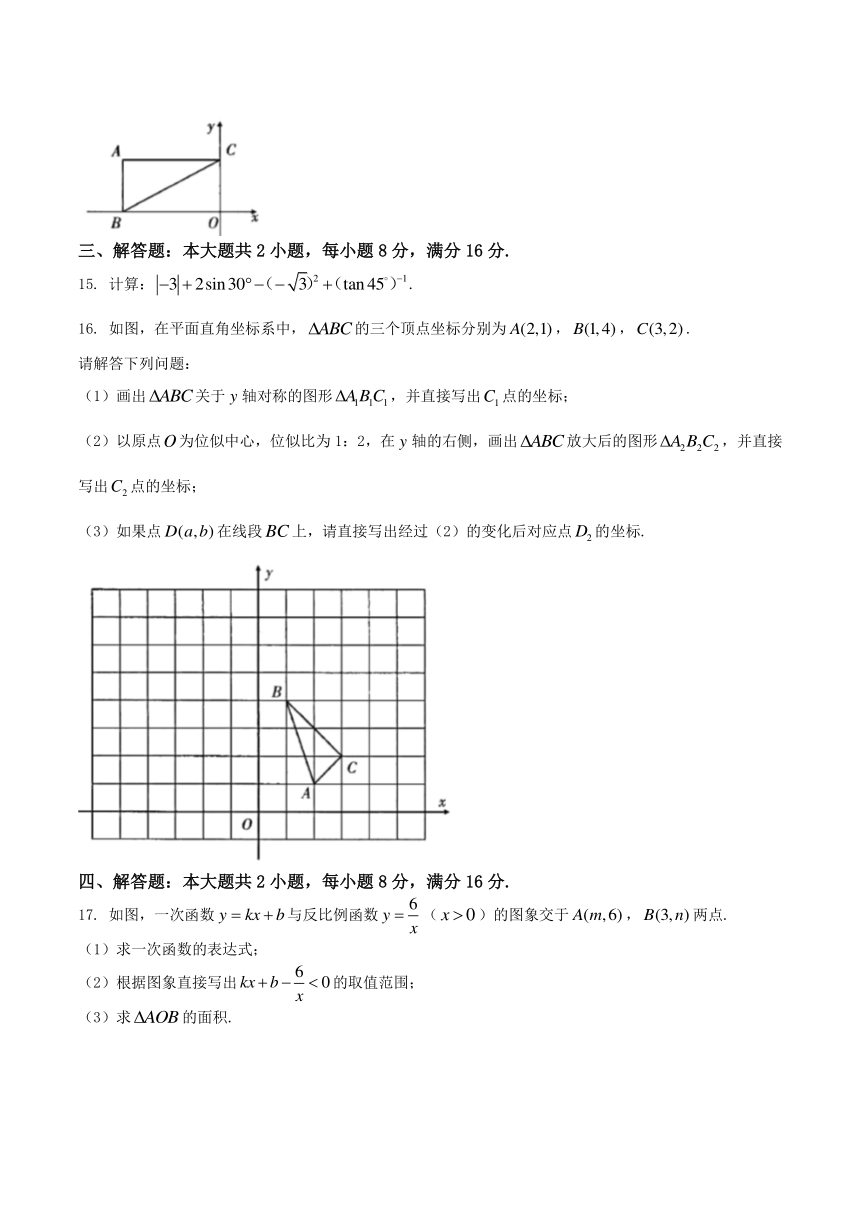
16. 如图,在平面直角坐标系中,的三个顶点坐标分别为,,.
请解答下列问题:
(1)画出关于轴对称的图形,并直接写出点的坐标;
(2)以原点为位似中心,位似比为1:2,在轴的右侧,画出放大后的图形,并直接写出点的坐标;
(3)如果点在线段上,请直接写出经过(2)的变化后对应点的坐标.
四、解答题:本大题共2小题,每小题8分,满分16分.
17. 如图,一次函数与反比例函数()的图象交于,两点.
(1)求一次函数的表达式;
(2)根据图象直接写出的取值范围;
(3)求的面积.
18. 如图,在锐角三角形中,点,分别在边,上,于点,于点..
(1)求证:∽;
(2)若,,求的值.
五、解答题:本大题共2小题,每小题10分,满分20分.
19. 为加快城乡对接,建设全域美丽乡村,某地区对、两地间的公路进行改建.如图,、两地之间有一座山,汽车原来从地到地需途径地沿折线行驶,现开通隧道后,汽车可直接沿直线行驶.已知,,.
(1)开通隧道前,汽车从地到地大约要走多少千米?
(2)开通隧道后,汽车从地到地大约可以少走多少千米?
(结果精确到0.1.参考数据:,)
20. 通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做底角的邻对().如图1,在中,,底角的邻对记作,这时,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解答下列问题:
(1) ;
(2)如图2,在中,,,,求的周长.
六、解答题:本题满分12分.
21. 如图,已知二次函数的图象经过,两点.
(1)求该抛物线的表达式及对称轴;
(2)当为何值时,?
(3)在轴的上方作平行于轴的直线,与抛物线交于,两点(点在对称轴的左侧),过点,作轴的垂线,垂足分别为,,当矩形为正方形时,求点的坐标.
七、解答题:本题满分12分.
22. 长丰县是国家无公害草莓生产示范基地,生产的草莓是安徽省特色水果,也是安徽省的特产之一.今年某水果销售店在草莓销售旺季,试销售成本为20元/的草莓,规定试销期间销售单价不低于成本单价,也不高于40元/,经试销发现,销售量()与销售单价(元)符合一次函数关系,如图是与的函数关系图象.
(1)求与的函数表达式;
(2)设该水果销售店试销草莓获得的利润为元,求的最大值.
八、解答题:本题满分14分.
23. 如图,在中,,,,动点从点出发,在边上以每秒2的速度向点匀速运动,同时动点从点出发,在边上以每秒的速度向点匀速运动,设运动时间为(),连接.
(1)若,求的值;
(2)若与相似,求的值;
(3)当为何值时,四边形的面积最小?并求出最小值.
试卷答案
一、选择题
1-5: CDBDA 6-10: DABCA
二、填空题
11. 12. -4 13. 14.或
三、解答题
15.解:原式
16.解:(1),如图所示,
(2),如图所示,
(3)
四、解答题
17. 解:(1)把,代入,得,.
∴,的坐标分别为,.
把,代入,得
,解得
∴一次函数的表达式为.
(2)或
(3)当时,一次函数.
∴.
18. (1)证明:,,
∴.
∴,
∴.
∴,
∴∽
(2)解:∵,,
∴.
由(1)知∽,
∴
∴
∴
∴
五、解答题
19.解:(1)如图,过点作,交于点.
∵,,,
∴
∵,
∴
∴
答:开通隧道前,汽车从地到地大约要走136.4.
(2)∵,,
∴
∵,,
∴
∴
∴.
答:开通隧道后,汽车从地到地大约可以少走27.2.
20. 解:(1)
(2)在中,∵,
∴
设,则.
过点作交于点.
∵
∴,
∵
∴,即
∴,
∴的周长.
六、解答题
21. 解:(1)∵二次函数的图象经过,,
∴,解得
∴该抛物线的表达式是.
∵,
∴对称轴为直线
(2)当时,.
解得,
∴抛物线与轴的交点坐标为,.
∴当时,.
(3)设点坐标为.
∵矩形是正方形,
∵点坐标为.
∵抛物线对称轴为直线,
∴点到对称轴距离等于点到对称轴距离.
∴.
解得,(不合题意舍去).
当时,.
∴点的坐标为
七、解答题
22. 解:(1)设与的函数表达式为.
根据题意,得,解得
∴与的函数表达式为().
(2)由题意,得
∵
∴当时,随的增大而增大.
又∵,
∴当时,有最大值,最大值为(元).
八、解答题
23. 解:(1)在中,∵,,,
∴,.
由题意知,,
∴.
由,得.
解得
(2)①当∽时,
得,即
解得.
②当∽时,
得,即
解得
∴当或时,与相似
(3)如图,过点作于点,则.
设四边形的面积为.
由题意,得
∵
∴当时,取最小值,
一、选择题:本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 抛物线的顶点坐标是( )
A. B. C. D.
2. 在中,,,,则长是( )
A.4 B.6 C.8 D.10
3. 将抛物线向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的表达式是( )
A. B.
C. D.
4. 关于反比例函数,下列说法正确的是( )
A.图象过点 B.图象在第一、三象限
C.当时,随的增大而减小 D.当时,随的增大而增大
5. 已知抛物线()经过,,,四点,则与的大小关系是( )
A. B. C. D.不能确定
6. 如图,在中,为的中点,为的中点,的延长线交于点,则的值是( )
A.1:5 B.1:4 C.1:3 D.1:2
7. 一次函数和反比例函数在同一个平面直角坐标系中的图象如图所示,则二次函数的图象可能是( )
A. B. C. D.
8. 已知二次函数()的图象如图所示,并且关于的一元二次方程
有两个不相等的实数根,下列结论:①;②;③;④.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
9. 如图,在等腰中,,,是上一点,若,则的长是( )
A. B. C.2 D.1
10. 如图,正方形的边长为2,动点,同时从点出发,在正方形的边上,分别按,的方向,都以1的速度运动,到达点运动终止,连接,设运动时间为,的面积为,则下列图象中能大致表示与的函数关系的是( )
A. B.
C. D.
二、填空题(本大题共4小题,每题5分,满分20分,将答案填在答题纸上)
11. 若,则 .
12. 如图,为反比例函数图象上的一点,轴于点,点在轴上,若,则的值为 .
13. 如图,将一副三角尺按如图所示叠放在一起,则的值是 .
14. 如图,平面直角坐标系中,矩形的边,分别在轴,轴上,点的坐标为,点在矩形的内部,点在边上,满足∽,当是等腰三角形时,点的坐标为 .
三、解答题:本大题共2小题,每小题8分,满分16分.
15. 计算:.
16. 如图,在平面直角坐标系中,的三个顶点坐标分别为,,.
请解答下列问题:
(1)画出关于轴对称的图形,并直接写出点的坐标;
(2)以原点为位似中心,位似比为1:2,在轴的右侧,画出放大后的图形,并直接写出点的坐标;
(3)如果点在线段上,请直接写出经过(2)的变化后对应点的坐标.
四、解答题:本大题共2小题,每小题8分,满分16分.
17. 如图,一次函数与反比例函数()的图象交于,两点.
(1)求一次函数的表达式;
(2)根据图象直接写出的取值范围;
(3)求的面积.
18. 如图,在锐角三角形中,点,分别在边,上,于点,于点..
(1)求证:∽;
(2)若,,求的值.
五、解答题:本大题共2小题,每小题10分,满分20分.
19. 为加快城乡对接,建设全域美丽乡村,某地区对、两地间的公路进行改建.如图,、两地之间有一座山,汽车原来从地到地需途径地沿折线行驶,现开通隧道后,汽车可直接沿直线行驶.已知,,.
(1)开通隧道前,汽车从地到地大约要走多少千米?
(2)开通隧道后,汽车从地到地大约可以少走多少千米?
(结果精确到0.1.参考数据:,)
20. 通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做底角的邻对().如图1,在中,,底角的邻对记作,这时,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解答下列问题:
(1) ;
(2)如图2,在中,,,,求的周长.
六、解答题:本题满分12分.
21. 如图,已知二次函数的图象经过,两点.
(1)求该抛物线的表达式及对称轴;
(2)当为何值时,?
(3)在轴的上方作平行于轴的直线,与抛物线交于,两点(点在对称轴的左侧),过点,作轴的垂线,垂足分别为,,当矩形为正方形时,求点的坐标.
七、解答题:本题满分12分.
22. 长丰县是国家无公害草莓生产示范基地,生产的草莓是安徽省特色水果,也是安徽省的特产之一.今年某水果销售店在草莓销售旺季,试销售成本为20元/的草莓,规定试销期间销售单价不低于成本单价,也不高于40元/,经试销发现,销售量()与销售单价(元)符合一次函数关系,如图是与的函数关系图象.
(1)求与的函数表达式;
(2)设该水果销售店试销草莓获得的利润为元,求的最大值.
八、解答题:本题满分14分.
23. 如图,在中,,,,动点从点出发,在边上以每秒2的速度向点匀速运动,同时动点从点出发,在边上以每秒的速度向点匀速运动,设运动时间为(),连接.
(1)若,求的值;
(2)若与相似,求的值;
(3)当为何值时,四边形的面积最小?并求出最小值.
试卷答案
一、选择题
1-5: CDBDA 6-10: DABCA
二、填空题
11. 12. -4 13. 14.或
三、解答题
15.解:原式
16.解:(1),如图所示,
(2),如图所示,
(3)
四、解答题
17. 解:(1)把,代入,得,.
∴,的坐标分别为,.
把,代入,得
,解得
∴一次函数的表达式为.
(2)或
(3)当时,一次函数.
∴.
18. (1)证明:,,
∴.
∴,
∴.
∴,
∴∽
(2)解:∵,,
∴.
由(1)知∽,
∴
∴
∴
∴
五、解答题
19.解:(1)如图,过点作,交于点.
∵,,,
∴
∵,
∴
∴
答:开通隧道前,汽车从地到地大约要走136.4.
(2)∵,,
∴
∵,,
∴
∴
∴.
答:开通隧道后,汽车从地到地大约可以少走27.2.
20. 解:(1)
(2)在中,∵,
∴
设,则.
过点作交于点.
∵
∴,
∵
∴,即
∴,
∴的周长.
六、解答题
21. 解:(1)∵二次函数的图象经过,,
∴,解得
∴该抛物线的表达式是.
∵,
∴对称轴为直线
(2)当时,.
解得,
∴抛物线与轴的交点坐标为,.
∴当时,.
(3)设点坐标为.
∵矩形是正方形,
∵点坐标为.
∵抛物线对称轴为直线,
∴点到对称轴距离等于点到对称轴距离.
∴.
解得,(不合题意舍去).
当时,.
∴点的坐标为
七、解答题
22. 解:(1)设与的函数表达式为.
根据题意,得,解得
∴与的函数表达式为().
(2)由题意,得
∵
∴当时,随的增大而增大.
又∵,
∴当时,有最大值,最大值为(元).
八、解答题
23. 解:(1)在中,∵,,,
∴,.
由题意知,,
∴.
由,得.
解得
(2)①当∽时,
得,即
解得.
②当∽时,
得,即
解得
∴当或时,与相似
(3)如图,过点作于点,则.
设四边形的面积为.
由题意,得
∵
∴当时,取最小值,
同课章节目录
