椭圆及其标准方程 课件 21张PPT
文档属性
| 名称 | 椭圆及其标准方程 课件 21张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 12:28:39 | ||
图片预览







文档简介
(共21张PPT)
2.2.1椭圆及其标准方程
课题引入
课题引入
·
r
O
A
课题引入
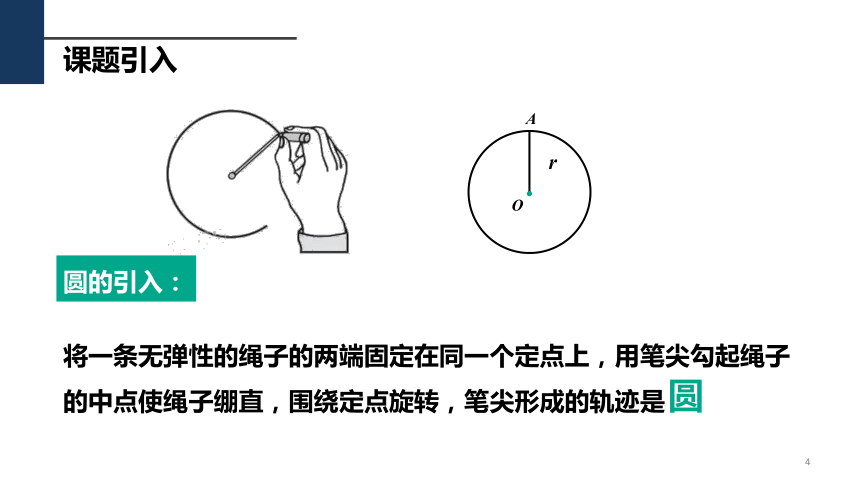
将一条无弹性的绳子的两端固定在同一个定点上,用笔尖勾起绳子的中点使绳子绷直,围绕定点旋转,笔尖形成的轨迹是
圆的引入:
圆
4
课题引入
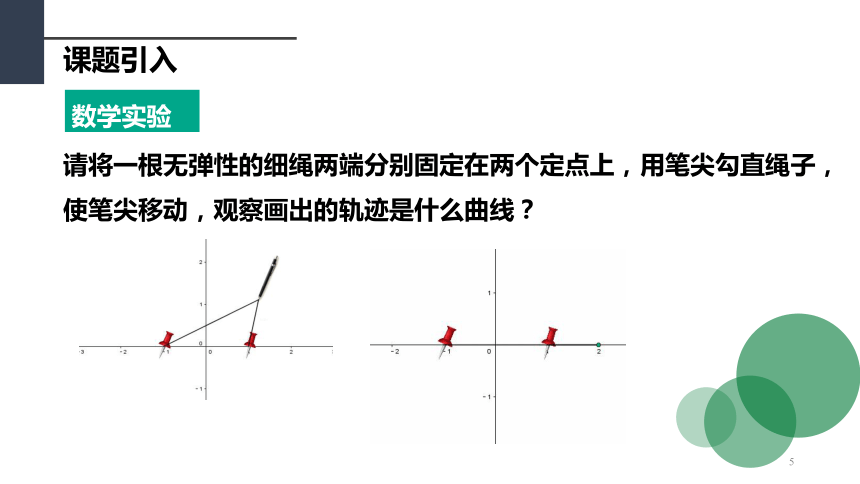
数学实验
请将一根无弹性的细绳两端分别固定在两个定点上,用笔尖勾直绳子,使笔尖移动,观察画出的轨迹是什么曲线?
5
课题引入
请回答以下问题:
视笔尖为动点,绳子两端为两定点,在运动过程中,动点始终满足什么条件不变的呢?
动点到两定点距离之和为绳长
6
新课讲授
一.椭圆的定义
F1
F2
M
平面内到两个定点F1、F2的距离之和等于
常数 的点的集合叫作椭圆。
当绳长=|F1F2|时,轨迹是
当绳长< |F1F2| 时,轨迹
不存在
线段F1F2
7
新课讲授
一.椭圆的定义
F1
F2
M
平面内到两个定点F1、F2的距离之和等于
常数 的点的集合叫作椭圆。
这两个定点F1,F2叫作椭圆的焦点
两个焦点F1,F2间的距离叫作椭圆的焦距
8
小试牛刀
例1:判断分别满足下列条件的动点M的轨迹是否为椭圆。
和点
的距离之和为6的点的轨迹;
(2)到点 和点 的距离之和为4的点的轨迹;
(3)到点 和点 的距离之和为6的点的轨迹;
(1)到点
(4)到点 和点 的距离之和为4的点的轨迹;
9
F1
F2
M
x
O
y
F1
F2
M
x
y
O
F1
F2
M
x
y
O
新课讲授
求圆的标准方程
的步骤:
(1) 建系
(2) 设点
(3) 限制条件
(4) 代入
(5) 化简检验
对称性
简洁性
10
求椭圆的标准方程
的步骤:
(1) 建系
(2) 设点
(3) 限制条件
(4) 代入
设 M(x,y) 是椭圆上任意一点
以直线F1F2 为 x 轴,线段 F1F2的垂直平分线为 y 轴,建立平面直角坐标系 。
设|F1F2|=2c,
(问题:接下来怎样化简?)
则有F1(-c,0)、F2(c,0)
新课讲授
F1
F2
M
x
O
y
(5) 化简检验
11
化简
移项得:
两边平方得:
新课讲授
12
两边再平方,得
整理得
移项,整理得
由椭圆定义可知
这说明椭圆上的点的坐标满足以上方程。我们还可以证明,这个方程的每一组解对应的点都在椭圆上。
新课讲授
椭圆的
标准方程
13
F1
F2
M
x
O
y
化简
移项得:
两边平方得:
新课讲授
14
两边再平方,得
整理得
移项,整理得
1
2
3
4
一般地,我们把中心在原点、焦点F1,F2在坐标轴上的椭圆的方程叫作椭圆的标准方程。
但是,一个椭圆,由于它在坐标平面内的位置不同,方程也不同,所以椭圆的标准方程还有其它形式。
对“标准”的理解:
F1
F2
M
F1
F2
M
x
o
y
新课讲授
15
新课讲授
焦点在y轴上的椭圆的标准方程是:
焦点在x 轴上的椭圆的标准方程是:
F1
F2
M
x
O
y
F2
F1
M
x
y
O
16
例题讲解
例2、判断下列椭圆的焦点在哪个坐标轴上,并写出焦点坐标 。
17
例3、已知椭圆的两个焦点的坐标分别是 , ,
椭圆上一点M到
的距离之和为4,求该椭圆的标准方程。
变式1:已知椭圆的两个焦点的坐标分别是 ,
椭圆上一点M到
的距离之和为4,求该椭圆的标准方程。
18
例题讲解
作业
《椭圆及其标准方程方程练习》
必做:1、2、3、4 选做:5
19
总结
定 义
标准方程
图象
焦点坐标
a,b,c的关系
F1
F2
M
x
o
y
F2
F1
M
x
y
o
20
数形结合思想,
分类讨论思想,
类比的方法
感谢聆听!
21
2.2.1椭圆及其标准方程
课题引入
课题引入
·
r
O
A
课题引入
将一条无弹性的绳子的两端固定在同一个定点上,用笔尖勾起绳子的中点使绳子绷直,围绕定点旋转,笔尖形成的轨迹是
圆的引入:
圆
4
课题引入
数学实验
请将一根无弹性的细绳两端分别固定在两个定点上,用笔尖勾直绳子,使笔尖移动,观察画出的轨迹是什么曲线?
5
课题引入
请回答以下问题:
视笔尖为动点,绳子两端为两定点,在运动过程中,动点始终满足什么条件不变的呢?
动点到两定点距离之和为绳长
6
新课讲授
一.椭圆的定义
F1
F2
M
平面内到两个定点F1、F2的距离之和等于
常数 的点的集合叫作椭圆。
当绳长=|F1F2|时,轨迹是
当绳长< |F1F2| 时,轨迹
不存在
线段F1F2
7
新课讲授
一.椭圆的定义
F1
F2
M
平面内到两个定点F1、F2的距离之和等于
常数 的点的集合叫作椭圆。
这两个定点F1,F2叫作椭圆的焦点
两个焦点F1,F2间的距离叫作椭圆的焦距
8
小试牛刀
例1:判断分别满足下列条件的动点M的轨迹是否为椭圆。
和点
的距离之和为6的点的轨迹;
(2)到点 和点 的距离之和为4的点的轨迹;
(3)到点 和点 的距离之和为6的点的轨迹;
(1)到点
(4)到点 和点 的距离之和为4的点的轨迹;
9
F1
F2
M
x
O
y
F1
F2
M
x
y
O
F1
F2
M
x
y
O
新课讲授
求圆的标准方程
的步骤:
(1) 建系
(2) 设点
(3) 限制条件
(4) 代入
(5) 化简检验
对称性
简洁性
10
求椭圆的标准方程
的步骤:
(1) 建系
(2) 设点
(3) 限制条件
(4) 代入
设 M(x,y) 是椭圆上任意一点
以直线F1F2 为 x 轴,线段 F1F2的垂直平分线为 y 轴,建立平面直角坐标系 。
设|F1F2|=2c,
(问题:接下来怎样化简?)
则有F1(-c,0)、F2(c,0)
新课讲授
F1
F2
M
x
O
y
(5) 化简检验
11
化简
移项得:
两边平方得:
新课讲授
12
两边再平方,得
整理得
移项,整理得
由椭圆定义可知
这说明椭圆上的点的坐标满足以上方程。我们还可以证明,这个方程的每一组解对应的点都在椭圆上。
新课讲授
椭圆的
标准方程
13
F1
F2
M
x
O
y
化简
移项得:
两边平方得:
新课讲授
14
两边再平方,得
整理得
移项,整理得
1
2
3
4
一般地,我们把中心在原点、焦点F1,F2在坐标轴上的椭圆的方程叫作椭圆的标准方程。
但是,一个椭圆,由于它在坐标平面内的位置不同,方程也不同,所以椭圆的标准方程还有其它形式。
对“标准”的理解:
F1
F2
M
F1
F2
M
x
o
y
新课讲授
15
新课讲授
焦点在y轴上的椭圆的标准方程是:
焦点在x 轴上的椭圆的标准方程是:
F1
F2
M
x
O
y
F2
F1
M
x
y
O
16
例题讲解
例2、判断下列椭圆的焦点在哪个坐标轴上,并写出焦点坐标 。
17
例3、已知椭圆的两个焦点的坐标分别是 , ,
椭圆上一点M到
的距离之和为4,求该椭圆的标准方程。
变式1:已知椭圆的两个焦点的坐标分别是 ,
椭圆上一点M到
的距离之和为4,求该椭圆的标准方程。
18
例题讲解
作业
《椭圆及其标准方程方程练习》
必做:1、2、3、4 选做:5
19
总结
定 义
标准方程
图象
焦点坐标
a,b,c的关系
F1
F2
M
x
o
y
F2
F1
M
x
y
o
20
数形结合思想,
分类讨论思想,
类比的方法
感谢聆听!
21
