【备考2020】中考数学一轮 第8章 相似形 8.1 相似三角形的性质与判定复习讲义(学生版+教师版)
文档属性
| 名称 | 【备考2020】中考数学一轮 第8章 相似形 8.1 相似三角形的性质与判定复习讲义(学生版+教师版) |  | |
| 格式 | zip | ||
| 文件大小 | 363.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 12:20:27 | ||
图片预览

文档简介
2020中考数学总复习 第八章 相似形
8.1 相似三角形的性质与判定
课标解读
1.了解比例的基本性质,了解线段的比及成比例线段.
2.认识相似图形,了解相似多边形的对应角相等,对应边成比例,面积比等于相似比的平方.
3.了解两个三角形相似的概念,掌握两个三角形相似的条件,能利用图形的相似解决一些实际问题.
4.了解图形的位似,能利用位似将一个图形放大或缩小.
知识梳理
知识点1相似三角形的胜质 1.相似三角形的对应角相等,对应边成比例 2.相似三角形的对应高的比、对应中线的比和对应角平分线的比都等于相似比. 3.相似三角形的周长比等于相似比. 4.相似三角形的面积比等于相似比的平方. 5.相似三角形的性质可用来证明线段成比例、角相等,也可用来求周长、边长等. 知识点2三角形相似的判定方法 1.定义法:对应角相等、对应边成比例的两个三角形相似. 2.平行法:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似. 3.判定定理:
(1)两角对应相等的两三角形相似. (2)两边对应成比例且夹角相等的两三角形相似.. (3)三条边对应成比例的两三角形相似.
知识点3:判定直角三角形相似的方法
1.一般三角形相似的方法均适用.
2.如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似. 3.直角三角形被斜边上的高分成的两个直角三角形与原三角形相似.
基础训练
1、如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
2、小明在打网球时,使球恰好能打过网,而且落点恰好在离网6米的位置上,则球拍击球的高度h为( )
A.米 B.1米 C.米 D.米
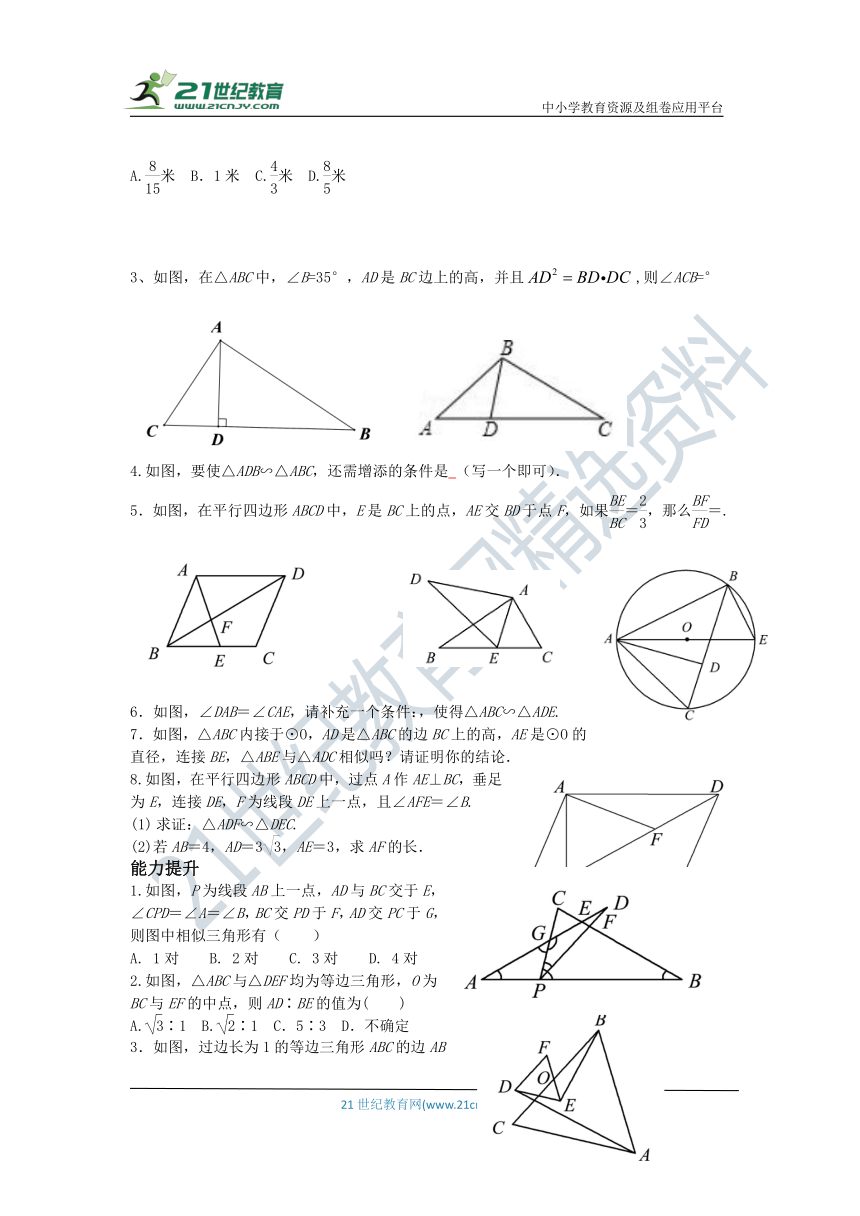
3、如图,在△ABC中,∠B=35°,AD是BC边上的高,并且,则∠ACB=°
4.如图,要使△ADB∽△ABC,还需增添的条件是 (写一个即可).
5.如图,在平行四边形ABCD中,E是BC上的点,AE交BD于点F,如果=,那么=.
6.如图,∠DAB=∠CAE,请补充一个条件:,使得△ABC∽△ADE.
7.如图,△ABC内接于⊙O,AD是△ABC的边BC上的高,AE是⊙O的直径,连接BE,△ABE与△ADC相似吗?请证明你的结论.
8.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
求证:△ADF∽△DEC.
(2)若AB=4,AD=3,AE=3,求AF的长.
能力提升
1.如图,P为线段AB上一点,AD与BC交于E,∠CPD=∠A=∠B,BC交PD于F,AD交PC于G,则图中相似三角形有( )
A. 1对 B. 2对 C. 3对 D. 4对
2.如图,△ABC与△DEF均为等边三角形,O为BC与EF的中点,则AD∶BE的值为( )
A.∶1 B.∶1 C.5∶3 D.不确定
3.如图,过边长为1的等边三角形ABC的边AB
上一点P,作PE⊥AC于E,Q为BC延长线上一点,
当PA=CQ时,连接PQ交AC边于D,则DE的长
为.
4.兴趣小组的同学要测量树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一 级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为.
5.如图,在矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF等于.
6.如图,一束光线从点A(3,3)出发,经过y轴上的C反射后经过点B (1,0),则光线从A点到B点经过的路线长是.
7.一块直角三角形形状的铁皮材料,两直角边长分别为30 cm、40 cm,现要把它加工成一个面积最大的正方形,两种加工方法如图①、②,请你用学过的知识说明哪种加工方法符合要求?
8.如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),
解答下列问题:
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR//BA交AC于点R,连结PR,当t为何值时,
△APR∽△PRQ?
中考真题
1.(2019,黄冈)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,连接OE.
(1)求证:△DBE是等腰三角形;
(2)求证:△COE∽△CAB.
8.1 相似三角形的性质与判定
课标解读
1.了解比例的基本性质,了解线段的比及成比例线段.
2.认识相似图形,了解相似多边形的对应角相等,对应边成比例,面积比等于相似比的平方.
3.了解两个三角形相似的概念,掌握两个三角形相似的条件,能利用图形的相似解决一些实际问题.
4.了解图形的位似,能利用位似将一个图形放大或缩小.
知识梳理
知识点1相似三角形的胜质 1.相似三角形的对应角相等,对应边成比例 2.相似三角形的对应高的比、对应中线的比和对应角平分线的比都等于相似比. 3.相似三角形的周长比等于相似比. 4.相似三角形的面积比等于相似比的平方. 5.相似三角形的性质可用来证明线段成比例、角相等,也可用来求周长、边长等. 知识点2三角形相似的判定方法 1.定义法:对应角相等、对应边成比例的两个三角形相似. 2.平行法:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似. 3.判定定理:
(1)两角对应相等的两三角形相似. (2)两边对应成比例且夹角相等的两三角形相似.. (3)三条边对应成比例的两三角形相似.
知识点3:判定直角三角形相似的方法
1.一般三角形相似的方法均适用.
2.如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似. 3.直角三角形被斜边上的高分成的两个直角三角形与原三角形相似.
基础训练
1、如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
2、小明在打网球时,使球恰好能打过网,而且落点恰好在离网6米的位置上,则球拍击球的高度h为( )
A.米 B.1米 C.米 D.米
3、如图,在△ABC中,∠B=35°,AD是BC边上的高,并且,则∠ACB=°
4.如图,要使△ADB∽△ABC,还需增添的条件是 (写一个即可).
5.如图,在平行四边形ABCD中,E是BC上的点,AE交BD于点F,如果=,那么=.
6.如图,∠DAB=∠CAE,请补充一个条件:,使得△ABC∽△ADE.
7.如图,△ABC内接于⊙O,AD是△ABC的边BC上的高,AE是⊙O的直径,连接BE,△ABE与△ADC相似吗?请证明你的结论.
8.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
求证:△ADF∽△DEC.
(2)若AB=4,AD=3,AE=3,求AF的长.
能力提升
1.如图,P为线段AB上一点,AD与BC交于E,∠CPD=∠A=∠B,BC交PD于F,AD交PC于G,则图中相似三角形有( )
A. 1对 B. 2对 C. 3对 D. 4对
2.如图,△ABC与△DEF均为等边三角形,O为BC与EF的中点,则AD∶BE的值为( )
A.∶1 B.∶1 C.5∶3 D.不确定
3.如图,过边长为1的等边三角形ABC的边AB
上一点P,作PE⊥AC于E,Q为BC延长线上一点,
当PA=CQ时,连接PQ交AC边于D,则DE的长
为.
4.兴趣小组的同学要测量树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一 级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为.
5.如图,在矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF等于.
6.如图,一束光线从点A(3,3)出发,经过y轴上的C反射后经过点B (1,0),则光线从A点到B点经过的路线长是.
7.一块直角三角形形状的铁皮材料,两直角边长分别为30 cm、40 cm,现要把它加工成一个面积最大的正方形,两种加工方法如图①、②,请你用学过的知识说明哪种加工方法符合要求?
8.如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),
解答下列问题:
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR//BA交AC于点R,连结PR,当t为何值时,
△APR∽△PRQ?
中考真题
1.(2019,黄冈)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,连接OE.
(1)求证:△DBE是等腰三角形;
(2)求证:△COE∽△CAB.
同课章节目录
