2019-2020学年北师大版数学必修三 第1章 统计 章末归纳总结课件(58张)
文档属性
| 名称 | 2019-2020学年北师大版数学必修三 第1章 统计 章末归纳总结课件(58张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 14:36:36 | ||
图片预览











文档简介
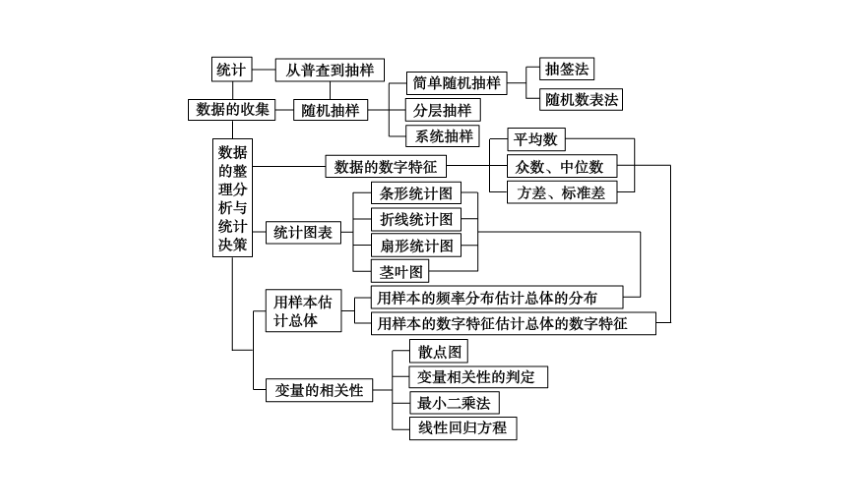
课件58张PPT。第一章统计章末归纳总结知 识 结 构知 识 梳 理1.随机抽样
统计分析的基本过程是:当总体容量很大或检测具有一定的破坏性时,可以从总体中抽取适当的样本,通过对样本的分析、研究,得到对总体的估计.
本章学习了三种比较典型和常用的抽样方法:简单随机抽样、分层抽样和系统抽样,它们的共同点:在抽样过程中每个个体被抽到的可能性(概率)相同,体现了抽样统计的客观性和公平性.
(1)简单随机抽样:在需要分析的总体中,随机地抽取一部分个体,然后对抽取的对象进行调查,并且在抽取的过程中,要保证每个个体被抽到的概率相等.这样的抽样方法叫作简单随机抽样.
简单随机抽样是抽样中一个最基本的方法,通常采用抽签法或随机数法.
(2)分层抽样:将总体按其属性特征分成若干类型(有时称为层),然后在每个类型中按照所占比例随机抽取一定的样本.这种抽样方法通常叫作分层抽样,有时也称为类型抽样.
(3)系统抽样:将总体的个体进行编号,按照简单随机抽样抽取第一个样本,然后按相同的间隔(称为抽样距)抽取其他样本,这种抽样方法叫作系统抽样,有时也称为等距抽样或机械抽样.2.用样本估计总体
(1)统计图表
①条形统计图、折线统计图、扇形统计图各自用途如下:条形统计图用于体现数据分布的频数及频率;扇形统计图用于体现部分在总体中所占比例;折线统计图用于体现数据的变化趋势.
②画茎叶图的步骤:将数据分为“茎”“叶”两部分→共茎的叶按从小到大(或从大到小)的顺序同行列出.
茎叶图只方便记录较少的样本数据,所有数据信息都可以从茎叶图中得到,方便记录与表示.
③画频率分布直方图的步骤:求给定一组数据的极差→决定组距与组数→分组→列频率分布表→画频率分布直方图.
频率分布直方图以面积的形式反映数据在各小组的频率的大小,能清楚反映数据分布的总体态势.
④频率折线图:在频率分布直方图中,按照分组原则,再在左边和右边各加一个区间.从所加的左边区间的中点开始,用线段依次连接各个矩形的顶端中点,直至右边所加区间的中点,就可以得到一条折线,即频率折线图.(3)用样本估计总体的方法
①用样本的频率分布估计总体的分布:通过样本数据得到频率分布表、频率分布直方图、频率折线图,对总体的频率分布作出估计.
②用样本的数字特征估计总体的数字特征:用样本数据的平均数、标准差估计总体的平均数、标准差.
从样本数据得到的分布、平均数和标准差并不是总体真正的分布、平均数和标准差,只是总体的一个估计,但这种估计是合理的.当样本量很大时,它们的确反映了总体的信息.3.变量的相关性
对两个变量的样本数据进行相关性分析,画出散点图,若所有点都在一条直线附近波动,则这两个变量是线性相关的,此时由用最小二乘法求出的a,b的计算公式专 题 探 究专题一 ?抽样方法的应用(3)应用三种抽样方法时需搞清楚它们的使用原则:
①当总体容量较小,样本容量较小时,制签简单,号签容易搅匀,可采用抽签法;
②当总体容量较大,样本容量较小时,可用随机数表法;
③当总体容量较大,样本容量也较大时,可用系统抽样法;
④当总体中个体差异较显著时,可采用分层抽样法.
[特别提醒]
在选取抽样方法时,必须使总体中每个个体被抽到的机会是均等的,同学们要理解各种抽样方法的特征及适用范围,在解题时灵活选用.〔跟踪练习1〕 在下列问题中,各采用什么抽样方法抽取样本较为合适?
(1)从20台彩电中抽取4台进行质量检验;
(2)科学会堂有32排,每排有40个座位(座位号为01~40),一次报告会坐满了听众,会后为了听取意见,留下了座位号为18的所有32名听众进行座谈;
(3)实验中学有180名教工,其中有专职教师144名,管理人员12名,后勤服务人员24名,今从中抽取一个容量为15的样本.
[解析] (1)因总体中的个体的数目较少,故采用简单随机抽样.
(2)因总体中的个体的数目较多,又是“等距”抽取,故采用系统抽样.
(3)因总体中的个体差异较大,故采用分层抽样.茎叶图是近年高考的热点. 主要考查茎叶图的画法,以及对茎叶图的分析和应用.
用茎叶图刻画数据有两个优点:一是所有的信息都可以从这个茎叶图中得到;二是茎叶图便于记录和表示,能够展示数据的分布情况,但当样本数据较多或数据位数较多时,茎叶图就显得不太方便了. 专题二 ?抽样方法的应用 某赛季甲、乙两名篮球运动员每场比赛的得分情况如下:
甲的得分:12,15,24,25,31,31,36,36,37,39,44,49,50;
乙的得分:8,13,14,16,23,26,28,33,38,39,51.
(1)画出甲、乙两名运动员得分数据的茎叶图;
(2)根据茎叶图分析甲、乙两名运动员的水平.[解析] (1)作出茎叶图如图.
(2)由上面的茎叶图可以看出,甲运动员的得分情况是大致对称的,中位数是36分;乙运动员的得分情况除一个特殊得分外,也大致对称,中位数是26分.因此甲运动员的发挥比较稳定,总体得分情况比乙运动员好.
〔跟踪练习2〕 在某电脑杂志的一篇文章中,每个句子所含的字数如下:
10,28,31,17,23,27,18,15,26,24,20,19,36,27,14,25,15,22,11,24,27,17.
在某报纸的一篇文章中,每个句子所含的字数如下:
27,39,33,24,28,19,32,41,33,27,35,12,36,41,27,13,22,23,18,46,32,22.
(1)将这两组数据用茎叶图表示;
(2)将这两组数据进行比较分析,得到什么结论?[解析] (1)茎叶图如图所示:
(2)电脑杂志上每个句子的字数集中在10~30之间,报纸上每个句子的字数集中在20~40之间,说明电脑杂志上每个句子的平均字数要比报纸上每个句子的平均字数要少,说明电脑杂志作为科普读物需要通俗易懂、简明.表现统计数字大小和变动的各种图形总称为统计图.其中有条形统计图、扇形统计图、折线统计图、茎叶图等.在统计学中把利用统计图形表现统计资料的方法叫作统计图示法.其特点是:形象具体、简明生动、通俗易懂、一目了然. 其主要用途有:表示现象间的对比关系;揭露总体结构;检查计划的执行情况;揭示现象间的依存关系,反映总体单位的分配情况;说明现象在空间上的分布情况.专题三 ?统计图表 某同学从一本英文杂志中截取了含有120个字母的一段小文章,欲研究六个字母的使用频率,我们不妨用1,2,3,4,5,6来代替这六个字母,发现它们出现的次数分别为18,19,21,22,20,20.
(1)列出样本数据的统计表;
(2)画出数据的条形统计图;
(3)画出数据的折线统计图.
[解析] (1)统计表如下:(2)数据的条形统计图如图所示.
(3)数据的折线统计图如图所示.〔跟踪练习3〕 小明家2018年的四个季度的用电量如下:其中各种电器用电量如下表:[解析] (1)折线统计图.
(2)扇形统计图.
(3)条形统计图.专题四 ?频率分布表与频率分布直方图 某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min),如下图是这次抽样的频率分布表和频率分布直方图,解答下列问题:(1)这次抽样的样本容量是多少?
(2)在表中填写出缺失的数据并补全频率分布直方图.
(3)旅客购票用时的平均数可能落在哪一小组?
(4)若每增加一个购票窗口可使平均购票用时降低5 min,要使平均购票用时不超过10 min,那么你估计最少要增加几个窗口?『规律总结』 本题考查了同学们整理数据和分析数据的能力,补全频率分布表可从横向(利用频数与频率的关系)和纵向(各组频数之和等于样本容量,各组频率之和等于1)两个角度进行突破.而频率分布直方图可利用小长方形的高的比即各组的频率之比来完成,近年来的高考对这方面的能力考查有明显加强的趋势.〔跟踪练习4〕 下表给出了某校500名12岁男孩中用随机抽样得出的120人的身高资料(单位:cm):
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)估计身高低于134 cm的人数占总人数的百分比.[解析] (1)列出样本的频率分布表如下:为了从整体上更好地把握总体的规律,我们还可以通过样本数据的众数、中位数、平均数和标准差等数字特征对总体的数字特征作出估计.众数就是样本数据中出现次数最多的数据.中位数就是把样本数据按照从小到大(或由大到小)排列,如果数据的个数是奇数,处于中间位置的数就是中位数;如果数据的个数是偶数,中间两个数据的平均数就是中位数.专题五 ?用样本的数字特征估计总体[特别提醒]
有时也用标准差的平方s2——方差来代替标准差,实质一样. 甲、乙两台机床在相同的技术条件下,同时生产一种零件,现在从中抽测10个,它们的尺寸分别如下(单位:mm).
甲机床:10.2 10.1 10 9.8 9.9 10.3 9.7 10 9.9 10.1;
乙机床:10.3 10.4 9.6 9.9 10.1 10.0 9.8 9.7 10.2 10.
分别计算上面两个样本的平均数和方差.图纸规定零件的尺寸为10 mm,从计算的结果来看哪台机床加工这种零件较合适?(要求利用公式进行笔算)『规律总结』 此题两机床生产零件尺寸的平均数相等都是10 mm,与规定尺寸相同,但方差不同,从方差可以估计出哪个机床加工的零件较合适.〔跟踪练习5〕 为了保护学生的视力,教室内的日光灯在使用一段时间后必须更换.已知某校使用的100只日光灯在必须换掉前的使用天数如下表:
(1)试估计这种日光灯的平均使用寿命;
(2)若定期更换,选择多长时间统一更换合适? 2018年某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:专题六 ?线性回归方程及应用
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程y=bx+a;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)题中所得的线性回归方程是否可靠?『规律总结』 建立回归模型的基本步骤:①确定研究对象,明确解释变量与预报变量;②画出确定好的解释变量与预报变量的散点图,观察它们之间的关系(如是否存在线性关系等);③由经验确定回归方程的类型(或数据呈线性关系,则选用线性回归方程y=bx+a);④按一定规则估计回归方程中的参数(如最小二乘法);⑤将所得的结果进行分析检验,看看是否符合实际情况.〔跟踪练习6〕 某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
(1)画出散点图;
(2)试求出线性回归方程;
(3)试根据(2)求出的线性回归方程,预测销售额为115万元时约需多少广告费?[解析] (1)散点图如图所示.(2)把数据列成表:a=50-6.5×5=17.5.
∴销售额y对支出x的回归直线方程为y=6.5x+17.5.
(3)根据求得的回归直线方程,当产品的预售额为115万元时,有115=0.65x+17.5,解得x=15.
答:预售额为115万元时,约需15万元广告费.
统计分析的基本过程是:当总体容量很大或检测具有一定的破坏性时,可以从总体中抽取适当的样本,通过对样本的分析、研究,得到对总体的估计.
本章学习了三种比较典型和常用的抽样方法:简单随机抽样、分层抽样和系统抽样,它们的共同点:在抽样过程中每个个体被抽到的可能性(概率)相同,体现了抽样统计的客观性和公平性.
(1)简单随机抽样:在需要分析的总体中,随机地抽取一部分个体,然后对抽取的对象进行调查,并且在抽取的过程中,要保证每个个体被抽到的概率相等.这样的抽样方法叫作简单随机抽样.
简单随机抽样是抽样中一个最基本的方法,通常采用抽签法或随机数法.
(2)分层抽样:将总体按其属性特征分成若干类型(有时称为层),然后在每个类型中按照所占比例随机抽取一定的样本.这种抽样方法通常叫作分层抽样,有时也称为类型抽样.
(3)系统抽样:将总体的个体进行编号,按照简单随机抽样抽取第一个样本,然后按相同的间隔(称为抽样距)抽取其他样本,这种抽样方法叫作系统抽样,有时也称为等距抽样或机械抽样.2.用样本估计总体
(1)统计图表
①条形统计图、折线统计图、扇形统计图各自用途如下:条形统计图用于体现数据分布的频数及频率;扇形统计图用于体现部分在总体中所占比例;折线统计图用于体现数据的变化趋势.
②画茎叶图的步骤:将数据分为“茎”“叶”两部分→共茎的叶按从小到大(或从大到小)的顺序同行列出.
茎叶图只方便记录较少的样本数据,所有数据信息都可以从茎叶图中得到,方便记录与表示.
③画频率分布直方图的步骤:求给定一组数据的极差→决定组距与组数→分组→列频率分布表→画频率分布直方图.
频率分布直方图以面积的形式反映数据在各小组的频率的大小,能清楚反映数据分布的总体态势.
④频率折线图:在频率分布直方图中,按照分组原则,再在左边和右边各加一个区间.从所加的左边区间的中点开始,用线段依次连接各个矩形的顶端中点,直至右边所加区间的中点,就可以得到一条折线,即频率折线图.(3)用样本估计总体的方法
①用样本的频率分布估计总体的分布:通过样本数据得到频率分布表、频率分布直方图、频率折线图,对总体的频率分布作出估计.
②用样本的数字特征估计总体的数字特征:用样本数据的平均数、标准差估计总体的平均数、标准差.
从样本数据得到的分布、平均数和标准差并不是总体真正的分布、平均数和标准差,只是总体的一个估计,但这种估计是合理的.当样本量很大时,它们的确反映了总体的信息.3.变量的相关性
对两个变量的样本数据进行相关性分析,画出散点图,若所有点都在一条直线附近波动,则这两个变量是线性相关的,此时由用最小二乘法求出的a,b的计算公式专 题 探 究专题一 ?抽样方法的应用(3)应用三种抽样方法时需搞清楚它们的使用原则:
①当总体容量较小,样本容量较小时,制签简单,号签容易搅匀,可采用抽签法;
②当总体容量较大,样本容量较小时,可用随机数表法;
③当总体容量较大,样本容量也较大时,可用系统抽样法;
④当总体中个体差异较显著时,可采用分层抽样法.
[特别提醒]
在选取抽样方法时,必须使总体中每个个体被抽到的机会是均等的,同学们要理解各种抽样方法的特征及适用范围,在解题时灵活选用.〔跟踪练习1〕 在下列问题中,各采用什么抽样方法抽取样本较为合适?
(1)从20台彩电中抽取4台进行质量检验;
(2)科学会堂有32排,每排有40个座位(座位号为01~40),一次报告会坐满了听众,会后为了听取意见,留下了座位号为18的所有32名听众进行座谈;
(3)实验中学有180名教工,其中有专职教师144名,管理人员12名,后勤服务人员24名,今从中抽取一个容量为15的样本.
[解析] (1)因总体中的个体的数目较少,故采用简单随机抽样.
(2)因总体中的个体的数目较多,又是“等距”抽取,故采用系统抽样.
(3)因总体中的个体差异较大,故采用分层抽样.茎叶图是近年高考的热点. 主要考查茎叶图的画法,以及对茎叶图的分析和应用.
用茎叶图刻画数据有两个优点:一是所有的信息都可以从这个茎叶图中得到;二是茎叶图便于记录和表示,能够展示数据的分布情况,但当样本数据较多或数据位数较多时,茎叶图就显得不太方便了. 专题二 ?抽样方法的应用 某赛季甲、乙两名篮球运动员每场比赛的得分情况如下:
甲的得分:12,15,24,25,31,31,36,36,37,39,44,49,50;
乙的得分:8,13,14,16,23,26,28,33,38,39,51.
(1)画出甲、乙两名运动员得分数据的茎叶图;
(2)根据茎叶图分析甲、乙两名运动员的水平.[解析] (1)作出茎叶图如图.
(2)由上面的茎叶图可以看出,甲运动员的得分情况是大致对称的,中位数是36分;乙运动员的得分情况除一个特殊得分外,也大致对称,中位数是26分.因此甲运动员的发挥比较稳定,总体得分情况比乙运动员好.
〔跟踪练习2〕 在某电脑杂志的一篇文章中,每个句子所含的字数如下:
10,28,31,17,23,27,18,15,26,24,20,19,36,27,14,25,15,22,11,24,27,17.
在某报纸的一篇文章中,每个句子所含的字数如下:
27,39,33,24,28,19,32,41,33,27,35,12,36,41,27,13,22,23,18,46,32,22.
(1)将这两组数据用茎叶图表示;
(2)将这两组数据进行比较分析,得到什么结论?[解析] (1)茎叶图如图所示:
(2)电脑杂志上每个句子的字数集中在10~30之间,报纸上每个句子的字数集中在20~40之间,说明电脑杂志上每个句子的平均字数要比报纸上每个句子的平均字数要少,说明电脑杂志作为科普读物需要通俗易懂、简明.表现统计数字大小和变动的各种图形总称为统计图.其中有条形统计图、扇形统计图、折线统计图、茎叶图等.在统计学中把利用统计图形表现统计资料的方法叫作统计图示法.其特点是:形象具体、简明生动、通俗易懂、一目了然. 其主要用途有:表示现象间的对比关系;揭露总体结构;检查计划的执行情况;揭示现象间的依存关系,反映总体单位的分配情况;说明现象在空间上的分布情况.专题三 ?统计图表 某同学从一本英文杂志中截取了含有120个字母的一段小文章,欲研究六个字母的使用频率,我们不妨用1,2,3,4,5,6来代替这六个字母,发现它们出现的次数分别为18,19,21,22,20,20.
(1)列出样本数据的统计表;
(2)画出数据的条形统计图;
(3)画出数据的折线统计图.
[解析] (1)统计表如下:(2)数据的条形统计图如图所示.
(3)数据的折线统计图如图所示.〔跟踪练习3〕 小明家2018年的四个季度的用电量如下:其中各种电器用电量如下表:[解析] (1)折线统计图.
(2)扇形统计图.
(3)条形统计图.专题四 ?频率分布表与频率分布直方图 某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min),如下图是这次抽样的频率分布表和频率分布直方图,解答下列问题:(1)这次抽样的样本容量是多少?
(2)在表中填写出缺失的数据并补全频率分布直方图.
(3)旅客购票用时的平均数可能落在哪一小组?
(4)若每增加一个购票窗口可使平均购票用时降低5 min,要使平均购票用时不超过10 min,那么你估计最少要增加几个窗口?『规律总结』 本题考查了同学们整理数据和分析数据的能力,补全频率分布表可从横向(利用频数与频率的关系)和纵向(各组频数之和等于样本容量,各组频率之和等于1)两个角度进行突破.而频率分布直方图可利用小长方形的高的比即各组的频率之比来完成,近年来的高考对这方面的能力考查有明显加强的趋势.〔跟踪练习4〕 下表给出了某校500名12岁男孩中用随机抽样得出的120人的身高资料(单位:cm):
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)估计身高低于134 cm的人数占总人数的百分比.[解析] (1)列出样本的频率分布表如下:为了从整体上更好地把握总体的规律,我们还可以通过样本数据的众数、中位数、平均数和标准差等数字特征对总体的数字特征作出估计.众数就是样本数据中出现次数最多的数据.中位数就是把样本数据按照从小到大(或由大到小)排列,如果数据的个数是奇数,处于中间位置的数就是中位数;如果数据的个数是偶数,中间两个数据的平均数就是中位数.专题五 ?用样本的数字特征估计总体[特别提醒]
有时也用标准差的平方s2——方差来代替标准差,实质一样. 甲、乙两台机床在相同的技术条件下,同时生产一种零件,现在从中抽测10个,它们的尺寸分别如下(单位:mm).
甲机床:10.2 10.1 10 9.8 9.9 10.3 9.7 10 9.9 10.1;
乙机床:10.3 10.4 9.6 9.9 10.1 10.0 9.8 9.7 10.2 10.
分别计算上面两个样本的平均数和方差.图纸规定零件的尺寸为10 mm,从计算的结果来看哪台机床加工这种零件较合适?(要求利用公式进行笔算)『规律总结』 此题两机床生产零件尺寸的平均数相等都是10 mm,与规定尺寸相同,但方差不同,从方差可以估计出哪个机床加工的零件较合适.〔跟踪练习5〕 为了保护学生的视力,教室内的日光灯在使用一段时间后必须更换.已知某校使用的100只日光灯在必须换掉前的使用天数如下表:
(1)试估计这种日光灯的平均使用寿命;
(2)若定期更换,选择多长时间统一更换合适? 2018年某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:专题六 ?线性回归方程及应用
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程y=bx+a;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)题中所得的线性回归方程是否可靠?『规律总结』 建立回归模型的基本步骤:①确定研究对象,明确解释变量与预报变量;②画出确定好的解释变量与预报变量的散点图,观察它们之间的关系(如是否存在线性关系等);③由经验确定回归方程的类型(或数据呈线性关系,则选用线性回归方程y=bx+a);④按一定规则估计回归方程中的参数(如最小二乘法);⑤将所得的结果进行分析检验,看看是否符合实际情况.〔跟踪练习6〕 某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
(1)画出散点图;
(2)试求出线性回归方程;
(3)试根据(2)求出的线性回归方程,预测销售额为115万元时约需多少广告费?[解析] (1)散点图如图所示.(2)把数据列成表:a=50-6.5×5=17.5.
∴销售额y对支出x的回归直线方程为y=6.5x+17.5.
(3)根据求得的回归直线方程,当产品的预售额为115万元时,有115=0.65x+17.5,解得x=15.
答:预售额为115万元时,约需15万元广告费.
