人教版九年级数学下册28.1 锐角三角函数复习课件(第4课时 共24张PPT)
文档属性
| 名称 | 人教版九年级数学下册28.1 锐角三角函数复习课件(第4课时 共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 391.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 22:14:16 | ||
图片预览




文档简介
课件24张PPT。
人教版 九年级数学下册
第28章 锐角三角函数
28.1 锐角三角函数(第4课时)
复习课
学习目标1.理解掌握锐角三角函数的概念;
2.熟记特殊锐角三角函数值,并能准确运用;
3.灵活运用锐角三角函数进行相关的运算。如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,求∠A的正弦、余弦、正切的值.解:在Rt△ABC中,∠C=90°
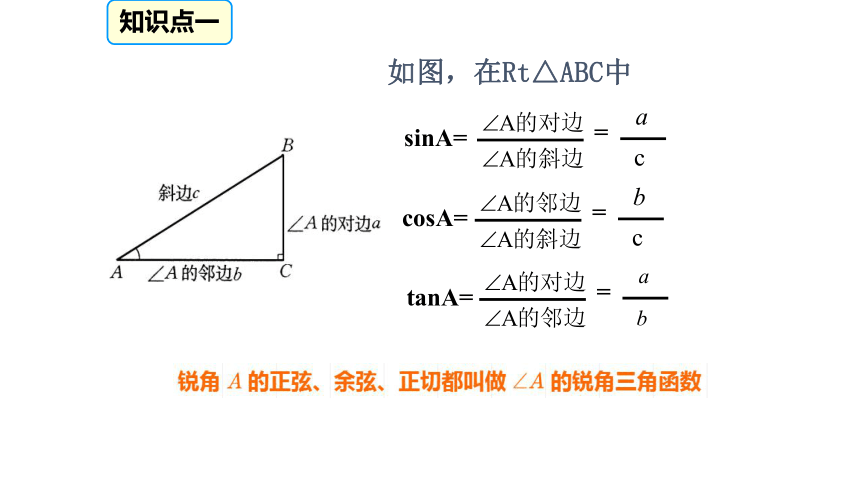
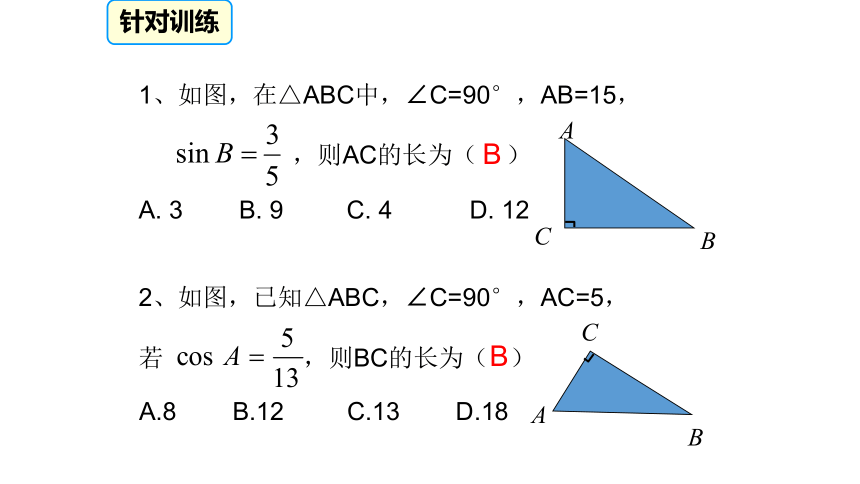
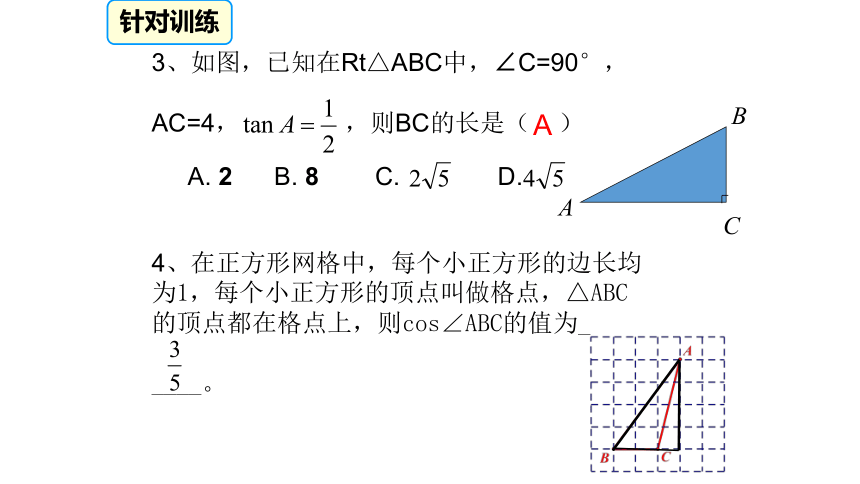
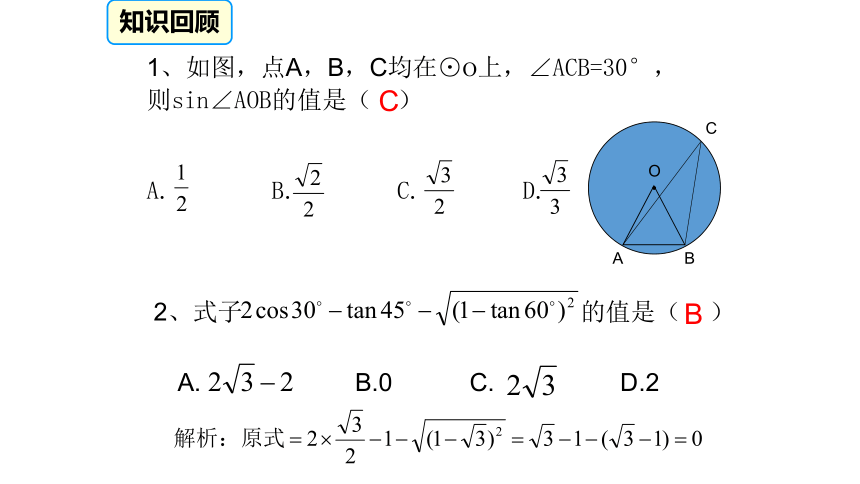
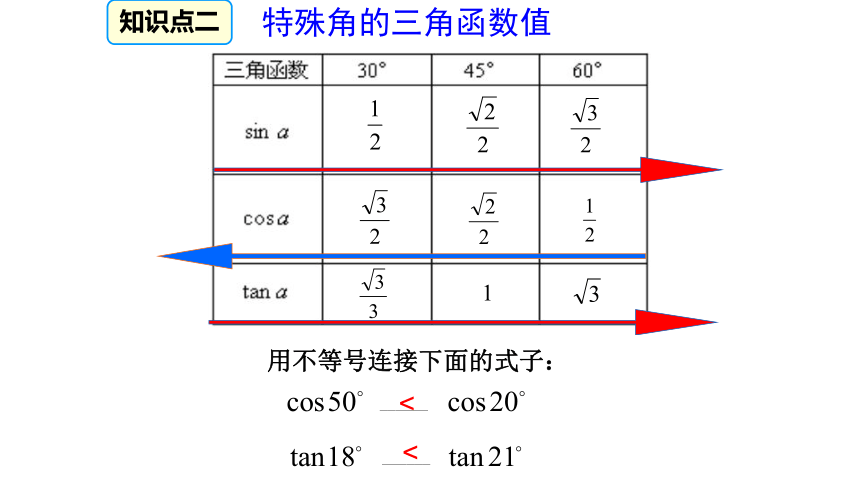
AC=4,BC=2,由勾股定理得:42知识回顾知识点一如图,在Rt△ABC中针对训练BB针对训练A知识回顾CB知识回顾B75°知识点二特殊角的三角函数值<<拓展补充特殊角的三角函数值2.互余的两角之间的三角函数关系拓展补充特殊角的三角函数值3.同角三角函数关系:
1.sin2α+cos2α=1
10拓展训练BB30°针对训练6.计算45°80°习题讲解解:习题讲解解:灵活运用1、已知:如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,求:(1)线段DC的长ABCDE解:在Rt△ABD中,由勾股定理得:灵活运用1、已知:如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,求:(2)tan∠EDC的值ABCDE解:在Rt△ADC中,点E为AC的中点灵活运用2、如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,AC=8,BC=6,求sin∠ABD的值OACBD分析:由同角的余角相等由同弧所对的圆周角相等等量代换∠ABD=∠ABC灵活运用2、如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,AC=8,BC=6,求sin∠ABD的值OACBD解:∵AB是⊙O的直径,∴∠ACB=90°在Rt△ABC中,AC=8,BC=6由勾股定理得:灵活运用3、如图,点O是Rt△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,当BC=3, 时,求AF的长.OACBDEF解:设⊙O的半径为r连接OE∴OE⊥AC 即∠AEO=90°在Rt△AOE中,OE=r∵⊙O与边AC相切于点E灵活运用4、如图,在四边形ABCD中,AB=AD,对角线AC,BD相交于点E,点O在线段AE上,⊙O过B,D两点,若OC=5,OB=3,且 ,求BC的长.解:∴AC垂直平分BD在Rt△BOE中,∵OB=3,连接OD,可得OB=OD课堂小结解
题
常
用
方
法(3)根据特殊角的三角函数值求值;(1)直接运用三角函数的定义求值;(4)借助边的数量关系求值;(6)借助等角求值;(5)根据三角函数关系求值;(2)构造直角三角形求值.家庭作业1.在Rt△ABC中,∠C=90°,BC=1,AB=2,则下列结论正确的是( ) C.
D.2.下列等式成立的是( )A.B. C.
D.A.B.3.如图,将∠AOB放在由边长为1的小正方形组成的网格中,则tan∠AOB=______4.已知α,β均为锐角,且满足______家庭作业5.计算:6.如图,在△ABC中,∠C=90°,点D,E分别在AC,AB上,
BD平分∠ABC,DE⊥AB,AE=6,求:(1)DE,CD的长;
(2)tan∠DBC的值
人教版 九年级数学下册
第28章 锐角三角函数
28.1 锐角三角函数(第4课时)
复习课
学习目标1.理解掌握锐角三角函数的概念;
2.熟记特殊锐角三角函数值,并能准确运用;
3.灵活运用锐角三角函数进行相关的运算。如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,求∠A的正弦、余弦、正切的值.解:在Rt△ABC中,∠C=90°
AC=4,BC=2,由勾股定理得:42知识回顾知识点一如图,在Rt△ABC中针对训练BB针对训练A知识回顾CB知识回顾B75°知识点二特殊角的三角函数值<<拓展补充特殊角的三角函数值2.互余的两角之间的三角函数关系拓展补充特殊角的三角函数值3.同角三角函数关系:
1.sin2α+cos2α=1
10拓展训练BB30°针对训练6.计算45°80°习题讲解解:习题讲解解:灵活运用1、已知:如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,求:(1)线段DC的长ABCDE解:在Rt△ABD中,由勾股定理得:灵活运用1、已知:如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,求:(2)tan∠EDC的值ABCDE解:在Rt△ADC中,点E为AC的中点灵活运用2、如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,AC=8,BC=6,求sin∠ABD的值OACBD分析:由同角的余角相等由同弧所对的圆周角相等等量代换∠ABD=∠ABC灵活运用2、如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,AC=8,BC=6,求sin∠ABD的值OACBD解:∵AB是⊙O的直径,∴∠ACB=90°在Rt△ABC中,AC=8,BC=6由勾股定理得:灵活运用3、如图,点O是Rt△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,当BC=3, 时,求AF的长.OACBDEF解:设⊙O的半径为r连接OE∴OE⊥AC 即∠AEO=90°在Rt△AOE中,OE=r∵⊙O与边AC相切于点E灵活运用4、如图,在四边形ABCD中,AB=AD,对角线AC,BD相交于点E,点O在线段AE上,⊙O过B,D两点,若OC=5,OB=3,且 ,求BC的长.解:∴AC垂直平分BD在Rt△BOE中,∵OB=3,连接OD,可得OB=OD课堂小结解
题
常
用
方
法(3)根据特殊角的三角函数值求值;(1)直接运用三角函数的定义求值;(4)借助边的数量关系求值;(6)借助等角求值;(5)根据三角函数关系求值;(2)构造直角三角形求值.家庭作业1.在Rt△ABC中,∠C=90°,BC=1,AB=2,则下列结论正确的是( ) C.
D.2.下列等式成立的是( )A.B. C.
D.A.B.3.如图,将∠AOB放在由边长为1的小正方形组成的网格中,则tan∠AOB=______4.已知α,β均为锐角,且满足______家庭作业5.计算:6.如图,在△ABC中,∠C=90°,点D,E分别在AC,AB上,
BD平分∠ABC,DE⊥AB,AE=6,求:(1)DE,CD的长;
(2)tan∠DBC的值
