3.4《力的合成》同步测试(含解析)
文档属性
| 名称 | 3.4《力的合成》同步测试(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 243.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-12 11:49:50 | ||
图片预览



文档简介
3.4力的合成
一、单选题
关于合力与其分力的关系,下列说法错误的是( )
A. 合力与其分力在作用效果上是等效的
B. 合力至少比某一个分力大
C. 合力可以比任意分力都小
D. 合力可以和两个分力的大小相等
若F1、F2是F的两个分力,则能表示F1、F2、F三者关系的是图(? ? )
A. ? B. ?
C. ? D.
小明想推动家里的衣橱,但使出了吃奶的力气也推不动,他便想了个妙招,如图所示,用A、B两块木板,搭成一个底角较小的人字形架,然后往中央一站,衣橱被推动了.下列说法中正确的是
A. 这是不可能的,因为小明根本没有用力去推衣橱
B. 这是不可能的,因为无论如何小明的力气也没那么大
C. 这有可能,A板对衣橱的推力有可能大于小明的重力
D. 这有可能,但A板对衣橱的推力不可能大于小明的重力
F1、F2是力F的两个分力,若F=15N,则下列不可能是F的两个分力的是( ? ? )
A. F1=25N F2=25 N B. F1=16 NF2=6 N
C. F1=12N F2=4 N D. F1=8 NF2=6 N
两个力F1和F2间的夹角为θ,两个力的合力为F,以下说法正确的是(??? )
若F1和F2大小不变,θ角越小,合力F就越小
B. 如果夹角θ不变,F1大小不变,若F2增大,合力F可能增大,也可能减小
C. 如果夹角θ不变,F1大小不变,只要F2增大,合力F必然增大
D. 合力F总比分力中的任何一个力都大
所示,轻绳OA、OB和OP将一只元宵花灯悬挂在P点,花灯保持静止.已知绳OA和OB的夹角为120°,对O点拉力的大小皆为F,轻绳OP对O点拉力的大小为( )
A. F B. F C. F D. 2F
F1、F2是两个共点力,两力的夹角是90°,其中F1=3N、F2=4N.这两个力的合力大小是( )
A. 1N B. 5N C. 6N D. 7N
最强台风“山竹”于不久前登陆我国东南沿海地区,中心附近最大风力可达到 14 级,不少公共设施都因台风而被破坏,如下图所示为太阳能路灯,它由太阳能电池板,LED 灯和灯柱组成.在台风来袭时,关于灯柱对LED 灯的作用力的说法正确的是( )
A.在受到台风水平作用时,风力恒定,灯柱对灯的作用力可能竖直向上
B. 在受到台风水平作用时,风力越强,灯柱对灯的作用力越大
C. 在受到台风水平作用时,风力越弱,灯所受到的合外力越小
D. 在无风干扰时,灯柱对灯的作用力方向斜向上
如图所示,某质点在共点力F1,F2,F3作用下处于静止状态,现将F1逆时针旋转60°,其它力均保持不变,那么该质点的合力大小为( )
A. F1 B. F2+F1 C. F3 D. F1+F3
如图,用两根等长轻绳将木板悬挂在竖直木桩上等高的两点,制成一简易秋千。某次维修时将两轻绳剪去一小段,但仍保持等长且悬挂点不变。木板静止时,F1表示木板所受合力的大小,F2表示单根轻绳对木板拉力的大小,则维修后:( )
A. F1不变,F2变大 B. F1不变,F2变小
C. F1变大,F2变大 D. F1变小,F2变小
二、多选题(本大题共3小题,共12.0分)
下列各组共面的三个共点力能使物体处于平衡状态的是( )
A. 5 N、7 N、8 N B. 5 N、1 N、3 N
C. 1 N、5 N、10 N D. 3 N、3 N、3 N
我国不少地方在节日期间有挂红灯笼的习俗.如图,质量为m的灯笼用两根不等长的轻绳OA、OB悬挂在水平天花板上,OA比OB长,O为结点.重力加速度大小为g.设OA、OB对O点的拉力分别为FA、FB,轻绳能够承受足够大的拉力,则( )
A. FA、FB的大小之和mg
B. 改变悬点A的位置,可使FA、FB都大于mg
C. 换质量更大的灯笼,FB的增加量比FA的增加量大
D. 如果两绳OA、OB能够承受的最大拉力相同,且绳长不变,把悬点B的位置缓慢往右移,则绳OA先拉断
在“探究求合力的方法”实验时以下说法正确的有( ).
A. 用两只弹簧秤拉橡皮条时,两细绳之间的夹角不宜过大
B. 用两只弹簧秤拉橡皮条时结点的位置与用一只弹簧秤拉橡皮条时结点的位置重合
C. 若用两只弹簧秤拉时合力的图示F与用一只弹簧秤拉时拉力的图示F′,不完全重合,说明力的合成的平行四边形定则不一定是普遍成立的
D. 若F1和F2的方向不变,而大小各增加1N,则合力F的方向不变,大小也增加1N
三、实验题
某同学做“验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮条的图钉,O为橡皮条与细绳的结点,OB和OC为细绳。图乙是在白纸上根据实验结果画出的图。
(1)下列叙述正确的是______(填选项前的字母)
A、同一实验过程中,结点的位置必须都拉到同一位置O点,不能随意变动
B、用两只弹簧测力计拉橡皮条时,应使两细绳之间的夹角为90o,以便算出合力的大小
C、两个分力之间的夹角越大越好
D、必须使分力与合力在同一平面内
(2)如果没有操作失误,图乙中的F与F′两力中,方向一定沿AO方向的是______。
(3)本实验采用的科学方法是______。
A.理想实验法???????B.等效替代法
C.控制变量法???????D.建立物理模型法
四、计算题
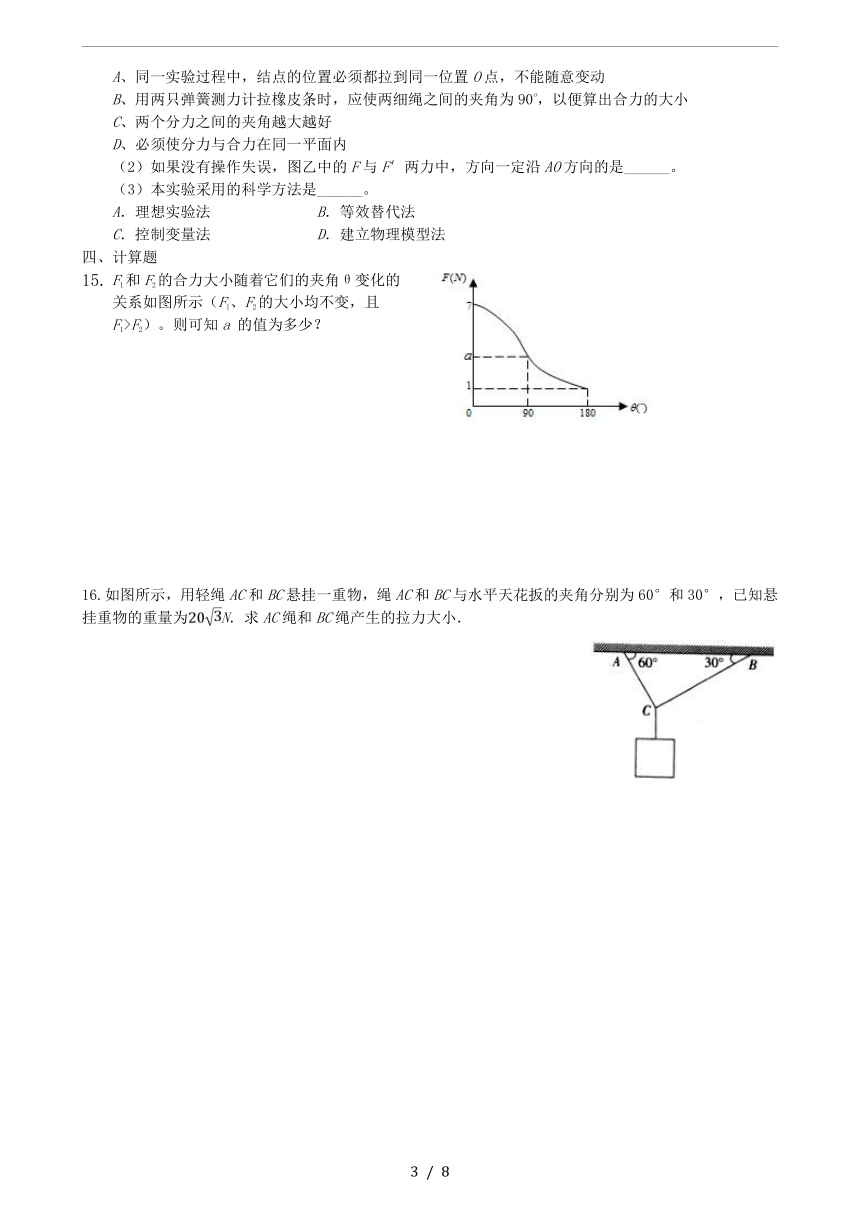
F1和F2的合力大小随着它们的夹角θ变化的关系如图所示(F1、F2的大小均不变,且F1>F2)。则可知a 的值为多少?
16.如图所示,用轻绳AC和BC悬挂一重物,绳AC和BC与水平天花扳的夹角分别为60°和30°,已知悬挂重物的重量为N.求AC绳和BC绳产生的拉力大小.
答案和解析
1.【答案】B
【解析】【分析】
如果二力在同一条直线上,根据力的合成计算合力的大小,即同一直线上同方向二力的合力等于二力之和,同一直线反方向二力的合力等于二力之差;如果二力不在同一条直线上,合力大小介于二力之和与二力之差之间。
本题主要考查合力与分力的关系。
【解答】
A.合力与分力的关系是等效替代的关系,等效说的就是相同的作用效果,故A正确;
BCD.根据矢量的合成法则知合力的大小可能大于任一分力,可能小于任一分力,可能等于某一分力,故B错误,CD正确。
本题选择错误的,故选B。
2.【答案】C
【解析】【分析】
平行四边形定则:以表示这两个力的线段为邻边作平行四边形,这两个力邻边的对角线就代表合力的大小和方向。
该题考查平行四边形定则的应用,正确理解分力与合力的关系是解答的关键。
【解答】
根据平行四边形定则可知,在F1、F2和F三者关系中,要以F1、F2为邻边,F为对角线,F的起点与两个分力F1、F2的起点是相同的。故C正确,ABD错误
故选C。
3.【答案】C
【解析】【分析】
这个要从力的分解角度来解释,将重力分解为沿人字形架斜向下的两个力;由于底角较小,根据三角函数关系得A板的作用力明显大于重力。
我们应该知道两个分力的合力可以远小于两个分力,也就是说用一个较小的力可以产生两个较大的分力。
【解答】
开始小明是推不动衣橱的,说明小明的推力小于最大静摩擦力;
站在人字形架时,重力产生两个效果,分别向左右两侧推墙壁和衣橱,如图:
小明的重力可以分解成沿A,B俩个方向的力,由于底角较小,所以A,B方向的力会很大。
A对衣橱的力可以分解成水平方向和竖直方向的力,而水平方向的力会远大于小明的重力;故C正确,ABD错误。
故选C。
4.【答案】D
【解析】【分析】
本题考查合力和分力之间的关系。合力F和两分力F1、F2之间的关系为|F1-F2|≤F≤|F1+F2|。
根据合力F和两分力F1、F2之间的关系|F1-F2|≤F≤|F1+F2|,求出两个力的合力范围,判断哪一组合力不可能为5N。
【解答】
A.根据|F1-F2|≤F≤|F1+F2|,25N和25N的合力范围为[0N,50N],可能为15N.故A正确;
B.根据|F1-F2|≤F≤|F1+F2|,16N和6N的合力范围为[10N,22N],可能为15N.故B正确;
C.根据|F1-F2|≤F≤|F1+F2|,12N和4N的合力范围为[8N,16N],可能为15N.故C正确;
D.根据|F1-F2|≤F≤|F1+F2|,8N和6N的合力范围为[2N,14N],不可能为15N.故D错误。
本题选不可能的,故选D。
5.【答案】B
【解析】【分析】
由力的合成方法可知,二力合成时,夹角越大,合力越小,两力合力的范围|F1-F2|≤F合≤F1+F2;一个合力与几个分力共同作用的效果相同,合力可以大于分力,可以小于分力,也可以等于分力。本题考查对合力与分力关系的理解能力,合力与分力是等效的,合力的范围在两个分力之差与之和之间.二力合成时,夹角越大,合力越小。
【解答】
A.若F1和F2大小不变,θ角越小,合力F越大,故A错误;
B.由力的合成方法可知,两力合力的范围|F1-F2|≤F合≤F1+F2,所以合力有可能大于任一分力,也可能小于任一分力,还可能与两个分力都相等,故B正确;
C.如果夹角不变,F1大小不变,只要F2增大,合力F可以减小,也可以增加,故C错误;
D.二力平衡时,合力为零,此时合力F比分力中的任何一个力都小,故D错误。
故选B。
6.【答案】A
【解析】略
7.【答案】B
【解析】解:勾股定理,F===5N,所以B正确,ACD错误。
故选:B。
F1、F2是两个互相垂直的共点力,根据勾股定理直接计算即可.
考查力的平行四边形定则,并掌握勾股定理的应用.
8.【答案】B
【解析】【分析】
对灯受力分析,根据平衡条件分析灯柱对灯的作用情况。
本题关键是对灯受力分析,根据平衡条件和力的合成分析。
【解答】
A.在受到台风水平作用时,风力恒定,灯受竖直向下的重力、灯柱的作用力、台风的水平作用力,三力平衡,所以灯柱对灯的作用力不可能竖直向上,故A错误;
BC.灯受竖直向下的重力G、灯柱的作用力F、台风的水平作用力F风,三力平衡,合力为零,则有:,所以风力越强,灯柱对灯的作用力越大,故B正确,C错误;
D.在无风干扰时,灯只受竖直向下的重力和灯柱对灯的作用力,二力平衡,所以灯柱对灯的作用力方向竖直向上。
?故选B。
9.【答案】A
【解析】【分析】
三力平衡中任意两个力的合力与第三个力等值、反向、共线,故先求出除F1外的两个力的合力,然后将转向后的力与除外的两个力的合力合成。
本题关键在于三力平衡中任意两个力的合力与第三个力等值、反向、共线;同时用到两个大小相等且互成120°的力合成时,合力在两个分力的角平分线上,且大小等于两分力。
【解答】
力平衡中任意两个力的合力与第三个力等值、反向、共线,故除外的两个力、的合力大小等于,方向与反向,故等效成物体受两个互成的大小等于的力作用;根据平行四边形定则可知,两个大小相等且互成的力合成时,合力在两个分力的角平分线上,大小等于分力,故此时物体所受到的合力大小为;故A正确,故BCD错误。
故选A。
10.【答案】A
【解析】【分析】
木板静止时,受重力和两个拉力而平衡,根据共点力平衡条件并结合力的合成分析即可。
本题是简单的三力平衡问题,关键是受力分析后运用图示法分析,不难。
【解答】
解:木板静止时,受重力和两个拉力而平衡,故三个力的合力为零,即:F1=0,不变;
根据共点力平衡条件,有:
2F2cosθ=mg
解得:
F2=
当细线变短时,细线与竖直方向的夹角θ增加,故cosθ减小,拉力F2变大.故A正确,BCD错误。
故选A。
11.【答案】AD
【解析】【分析】
三力合成,先将其中的两个力合成,再与第三个力合成,合成时,三力同向合力最大,两个力合成的合力有个范围,用与第三个力最接近的数值与第三个力合成求最小合力。
三力平衡,三个力中任意两个力的合力必然与第三个力等值、反向、共线。
【解答】
A .5N与7N合成最大12N,最小2N,当取8N时与第三个力合成,得到最小值为0N,故A正确;
B.1N和3N合成最大4N,最小2N,不可能为5N,故与第三个力不可能平衡,故B错误;
C.1N和5N合成最大6N,最小4N,不可能为10N,故与第三个力不可能平衡,故C错误;
D.3N和3N合成最小0N,最大6N,当取3N时,可能与第三个力平衡,故D正确;
故选AD。
12.【答案】BC
【解析】解:A、三角形的三条边代表FA、FB和mg的大小关系,两边之和大于第三边即FA、FB的大小之和大于mg。故A错误;
B、改变悬点A的位置,可以使FA、FB都大于mg即分力和合力的大小关系不确定,分力可以都大于合力,故B正确;
C、换质量更大的灯笼,由三角形相似可知:FB的增加量比FA的增加量大。故C正确;
D、由图象可知:FB>FA如果两绳OA、OB能够承受的最大拉力相同,且绳长不变,把悬点B的位置缓慢往右移,则绳OB先拉断,故D错误。
故选:BC。
对平行四边形定则的理解;通过图象分析出三个力的大小关系.
考查力的平行四边形定则.平行四边形实际是三角形,三角形的三条边的长短代表三个力的大小,两边之和大于第三边.理解合力与分力的关系.
13.【答案】AB
【解析】【分析】
正确解答本题需要掌握:理解“等效法”的具体应用;进行该实验的具体操作和注意事项;弹簧的示数以及夹角要大小适中,便于记录和作图即可。
实验中的具体步骤要本着简单易行,便于操作,有利于减小误差进行,所有操作步骤的设计都是以实验原理和实验目的为中心展开。
【解答】
A.实验中,把橡皮条的另一端拉到O点时,两细绳之间的夹角不宜过大,故A正确;
B.同一次实验过程中O点位置不允许变动,保证实验的等效性,用两只弹簧秤拉时结点的位置必须与用一只弹簧秤拉时结点的位置重合,故B正确;
C.实验存在一定的误差,若用两只弹簧秤拉时合力的图示F与用一只弹簧秤拉时拉力的图示F不完全重合,这是由实验误差造成的,并不能说明力的合成的平行四边形定则不一定是普遍成立的,故C错误;
D.只有当F1和F2同向时,才会出现大小各增加1N,合力F大小也增加1N的情况,故D错误。
故选AB。
14.【答案】AD ? F′ ? B
【解析】解:(1)A、同一实验过程中,结点的位置必须都拉到同一位置O点,不能随意变动,故A正确;
BC、此实验对F1、F2之间的夹角没有要求,通常在60°至120°之间最佳,故BC错误。
D、完成本实验时,弹簧秤、橡皮条、细绳方向必须与木板平面平行,且在同一平面内,这样才能确保力的准确性,故D正确。
故选:AD。
(2)F是由两个分力做出的合力的理论值,F′是实际测量的合力的值;由于误差的存在,所以F和F′方向并不完全重合,图乙中的F与F'两力中,方向一定沿AO方向的是F′。
(3)合力与分力是等效替代的关系,所以本实验采用的等效替代法。故ACD错误,B正确。
故选:B。
故答案为:(1)AD;(2)F′;(3)B
(1)在实验中F和F′分别由平行四边形定则及实验得出,明确理论值和实验值的区别即可正确解答;
(2)根据平行四边形定则的原理以及作图的方法判断;
(3)本实验中采用了两个力合力与一个力效果相同来验证的平行四边形定则,因此采用“等效法”,注意该实验方法的应用。
本题考查验证力的平行四边形定则,要求掌握其实验原理,熟悉操作步骤,牢记操作注意事项。
15.【答案】解:由图象知,当F1、F2成0°角时,两个力的合力为F1+F2,当两个力成180°时,两个力的合力为F1-F2(F1>F2)
由图象得:
F1+F2=7N????? ①
F1-F2=1N????? ②
由①式和②式可得:F1=4N;F2=3N
当两力夹角为90°时a==5N。
【解析】正确的读图,根据力的合成定则求解即可,两个力成0°角时,即两个力的方向相同,成180°时两个力的方向相反。
?熟悉图象,能读懂图象所给出的物理信息,由力合成的平行四边形定则可得。
16.【答案】解:对结点受力分析可知,结点受物体的拉力、两绳子的拉力而处于平衡状态;
由几何关系可知:cos30°=
解得:FAC=Gcos30°=20×=30N;
sin30°=
得:FBC=Gsin30°=10N.
答:绳AC的拉力为30N;绳BC的拉力为10N.
【解析】以结点为研究对象,由共点力的平衡条件可得出几何关系,由公式可得出拉力.
共点力的平衡类题目关键在于正确的受力分析,由几何关系求解.当力3个力时一般用合成法,若超过3个一般用正交分解法.
PAGE / NUMPAGES
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
