沪科版八下:17.5 一元二次方程的应用 教案(表格式,2课时)
文档属性
| 名称 | 沪科版八下:17.5 一元二次方程的应用 教案(表格式,2课时) |
|
|
| 格式 | doc | ||
| 文件大小 | 126.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 11:55:52 | ||
图片预览


文档简介
17.5一元二次方程的应用(1)
主备人:
时间
地点
召集人
课题 17.5一元二次方程的应用(1) 课时 第 1 课时
(总第 1 课时) 科任教师
教学 目标 知识与技能:
1.巩固列方程解应用题的方法步骤。
2.解决与面积有关的实际问题。
3.了解如何建立数学模型,解决与一元二次方程有关的实际应用题。
过程与方法:通过自主探索、合作交流等活动,发展学生数学思维,培养学生合作学习意识、动手、动脑习惯,激发学生学习热情。
情感态度与价值观:使学生认识到数学与生活紧密相连,让他们在学习活动中获得成功的体验,建立自信心,从而使学生更加热爱数学、热爱生活.
重难点 重点:列一元二次方程解应用题.
难点:将实际问题提炼成数学问题.
教
学
过
程
教
学
过
程
一、学习目标(2分钟)
1.巩固列方程解应用题的方法步骤。
2.解决与面积有关的实际问题。
3.了解如何建立数学模型,解决与一元二次方程有关的实际应用题。
二、自学提纲:(10分钟)
1.列方程解应用题的一般步骤是什么?
2.自学,并回答下列问题:
(1)路的面积怎样计算?花坛的面积怎样计算?
(2)本题的相等关系是什么?
(3)本题的解决方法有几种,哪种方法更简便?
(4)依据什么检验方程的根?
三、合作探究(15分钟)
知识点归纳: 列一元二次方程解应用题的一般步骤与列一元一次方程解应用题一样,所以列一元二次方程解应用题的一般步骤也归纳为:审、设、列、解、验、答这六个步骤.
例题探究:例1 在一块宽20 m,长32 m的长方形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),
把长方形空地分成大小一样的6块,建成小花坛,如图:
要使花坛的总面积为570(图中长度的单位:m),问
小路的宽应是多少?
解法(一)相等关系式为:
长方形总面积—小路的面积=花坛面积.
解法(二)当我们把三条小路都平行移动到长方形的一边,使6块花坛的面积集中起来,这样一来,花坛的长为(32-2x)m,宽为(20-x)m,则相等关系式为:
花坛的长×花坛的宽=花坛的面积
即:
举一反三:
例1 如图,有一块长40m,宽30m的长方形铁片,在它的四周
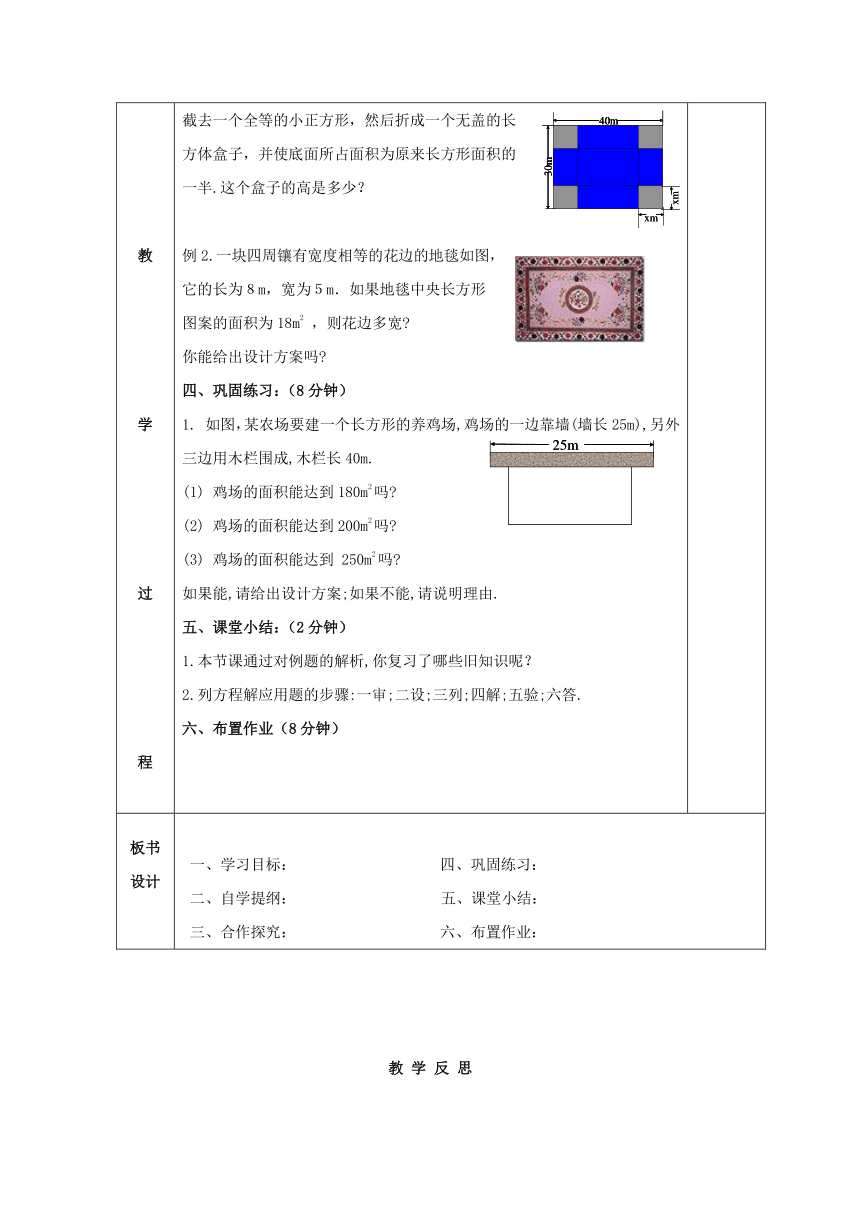
截去一个全等的小正方形,然后折成一个无盖的长
方体盒子,并使底面所占面积为原来长方形面积的
一半.这个盒子的高是多少?
例2.一块四周镶有宽度相等的花边的地毯如图,
它的长为8m,宽为5m.如果地毯中央长方形
图案的面积为18m2 ,则花边多宽?
你能给出设计方案吗?
四、巩固练习:(8分钟)
1. 如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长25m),另外三边用木栏围成,木栏长40m.
(1) 鸡场的面积能达到180m2吗?
(2) 鸡场的面积能达到200m2吗?
(3) 鸡场的面积能达到 250m2吗?
如果能,请给出设计方案;如果不能,请说明理由.
五、课堂小结:(2分钟)
1.本节课通过对例题的解析,你复习了哪些旧知识呢?
2.列方程解应用题的步骤:一审;二设;三列;四解;五验;六答.
六、布置作业(8分钟) 讨论补充记录
讨论补充记录
板书 设计
一、学习目标: 四、巩固练习:
二、自学提纲: 五、课堂小结:
三、合作探究: 六、布置作业:
教 学 反 思
17.5一元二次方程的应用(2)
主备人:
时间
地点
召集人
课题 17.5一元二次方程的应用(2) 课时 第 2 课时
(总第 2 课时) 科任教师
教学 目标 知识与技能:1.使学生会用列一元二次方程的方法解决有关增长率、降低率问题.
2.进一步培养学生用一元二次方程解决实际问题的能力。
过程与方法:通过自主探索、合作交流等活动,发展学生数学思维,培养学生合作学习意识、动手、动脑习惯,激发学生学习热情。
情感态度与价值观:使学生认识到数学与生活紧密相连,让他们在学习活动中获得
成功的体验,建立自信心,从而使学生更加热爱数学、热爱生活.
重难点 重点:列一元二次方程解应用题.
难点:将实际问题提炼成数学问题.
一、学习目标(2分钟)
会用列一元二次方程的方法解决有关增长率、降低率问题.
二、自学提纲:(10分钟)
自学课本内容,与同学们合作交流以下问题:
1.这两题有共同点吗?
2.原产量(基数)是多少?增产量怎么计算?实际产量是多少,
怎么计算?
3.你能归纳出这类问题的等量关系式吗?
三、合作探究(15分钟)
问题1
某地为增加农民收入,需要调整农作物种植结构,计划2017年无公害蔬菜的产量比2015年翻一番,要实现这一目标,2016年和2017年无公害蔬菜产量的年平均增长率应是多少?
分析:设无公害蔬菜的年平均增长率为x,2015年的产量为a.则
2016年的增产量为 _______;实际产量为___________;
2017的增产量为__________;实际产量为___________;
列方程为___________________________________;
例2
利民大药房将原来每盒盈利30%的某种药品,先后两次降价,经两次降价后每盒仍能盈利10%,求这两次降价的平均降价率是多少?
分析:设某种药品进价是a元/盒,零售价按盈利30%定价
就是_________________元/盒,两次降价后仍能盈利10%,
就是_________________元/盒,设两次平均降价率是x,
则第一次降价后的零售价为___________________________,
第二次降价后的零售价为____________________________
列方程得:_____________.
归纳:
设基数为a,平均增长率为x,
则一次增长后的值为_____________;
二次增长后的值为_____________________;
依次类推n次增长后的值为_________________.
求降低率时,则是把“+”号改为“-”号。
四、巩固练习:(8分钟)
1.乐清花鸟市场去年一月份花苗销售额为60万元,二月份由于某种原因,销售额下降了10%,以后改进管理,增加品种数量,月销售额大幅上升,到四月份销售额猛增到96万元,求三、四月份平均每月增长的百分率是多少?(精确到0.1%)
2.某校为美化校园,逐年扩大校园绿化面积.据统计,今年的绿化面积是前年绿化面积的1.25倍,那么这两年平均每年校园绿化面积增加的百分率是多少(精确到1℅)?
提示:增长率问题中若基数不明确,通常可设为“1”,或设为a等。
五、课堂小结:(2分钟)
本节课,你学到了哪些知识?
1.列一元二次方程解应用题的基本步骤:
审 设 列 解 验 答
2.增长率(降低率)问题:
设基数为a,平均增长率为x,
a(1+x)n =n次增长后的值
a(1-x)n =n次降低后的值
六、布置作业:(8分钟) 讨论补充记
录
讨论补充记
录
一、学习目标: 四、巩固练习:
二、自学提纲: 五、课堂小结:
三、合作探究: 六、布置作业:
教 学 反 思
主备人:
时间
地点
召集人
课题 17.5一元二次方程的应用(1) 课时 第 1 课时
(总第 1 课时) 科任教师
教学 目标 知识与技能:
1.巩固列方程解应用题的方法步骤。
2.解决与面积有关的实际问题。
3.了解如何建立数学模型,解决与一元二次方程有关的实际应用题。
过程与方法:通过自主探索、合作交流等活动,发展学生数学思维,培养学生合作学习意识、动手、动脑习惯,激发学生学习热情。
情感态度与价值观:使学生认识到数学与生活紧密相连,让他们在学习活动中获得成功的体验,建立自信心,从而使学生更加热爱数学、热爱生活.
重难点 重点:列一元二次方程解应用题.
难点:将实际问题提炼成数学问题.
教
学
过
程
教
学
过
程
一、学习目标(2分钟)
1.巩固列方程解应用题的方法步骤。
2.解决与面积有关的实际问题。
3.了解如何建立数学模型,解决与一元二次方程有关的实际应用题。
二、自学提纲:(10分钟)
1.列方程解应用题的一般步骤是什么?
2.自学,并回答下列问题:
(1)路的面积怎样计算?花坛的面积怎样计算?
(2)本题的相等关系是什么?
(3)本题的解决方法有几种,哪种方法更简便?
(4)依据什么检验方程的根?
三、合作探究(15分钟)
知识点归纳: 列一元二次方程解应用题的一般步骤与列一元一次方程解应用题一样,所以列一元二次方程解应用题的一般步骤也归纳为:审、设、列、解、验、答这六个步骤.
例题探究:例1 在一块宽20 m,长32 m的长方形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),
把长方形空地分成大小一样的6块,建成小花坛,如图:
要使花坛的总面积为570(图中长度的单位:m),问
小路的宽应是多少?
解法(一)相等关系式为:
长方形总面积—小路的面积=花坛面积.
解法(二)当我们把三条小路都平行移动到长方形的一边,使6块花坛的面积集中起来,这样一来,花坛的长为(32-2x)m,宽为(20-x)m,则相等关系式为:
花坛的长×花坛的宽=花坛的面积
即:
举一反三:
例1 如图,有一块长40m,宽30m的长方形铁片,在它的四周
截去一个全等的小正方形,然后折成一个无盖的长
方体盒子,并使底面所占面积为原来长方形面积的
一半.这个盒子的高是多少?
例2.一块四周镶有宽度相等的花边的地毯如图,
它的长为8m,宽为5m.如果地毯中央长方形
图案的面积为18m2 ,则花边多宽?
你能给出设计方案吗?
四、巩固练习:(8分钟)
1. 如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长25m),另外三边用木栏围成,木栏长40m.
(1) 鸡场的面积能达到180m2吗?
(2) 鸡场的面积能达到200m2吗?
(3) 鸡场的面积能达到 250m2吗?
如果能,请给出设计方案;如果不能,请说明理由.
五、课堂小结:(2分钟)
1.本节课通过对例题的解析,你复习了哪些旧知识呢?
2.列方程解应用题的步骤:一审;二设;三列;四解;五验;六答.
六、布置作业(8分钟) 讨论补充记录
讨论补充记录
板书 设计
一、学习目标: 四、巩固练习:
二、自学提纲: 五、课堂小结:
三、合作探究: 六、布置作业:
教 学 反 思
17.5一元二次方程的应用(2)
主备人:
时间
地点
召集人
课题 17.5一元二次方程的应用(2) 课时 第 2 课时
(总第 2 课时) 科任教师
教学 目标 知识与技能:1.使学生会用列一元二次方程的方法解决有关增长率、降低率问题.
2.进一步培养学生用一元二次方程解决实际问题的能力。
过程与方法:通过自主探索、合作交流等活动,发展学生数学思维,培养学生合作学习意识、动手、动脑习惯,激发学生学习热情。
情感态度与价值观:使学生认识到数学与生活紧密相连,让他们在学习活动中获得
成功的体验,建立自信心,从而使学生更加热爱数学、热爱生活.
重难点 重点:列一元二次方程解应用题.
难点:将实际问题提炼成数学问题.
一、学习目标(2分钟)
会用列一元二次方程的方法解决有关增长率、降低率问题.
二、自学提纲:(10分钟)
自学课本内容,与同学们合作交流以下问题:
1.这两题有共同点吗?
2.原产量(基数)是多少?增产量怎么计算?实际产量是多少,
怎么计算?
3.你能归纳出这类问题的等量关系式吗?
三、合作探究(15分钟)
问题1
某地为增加农民收入,需要调整农作物种植结构,计划2017年无公害蔬菜的产量比2015年翻一番,要实现这一目标,2016年和2017年无公害蔬菜产量的年平均增长率应是多少?
分析:设无公害蔬菜的年平均增长率为x,2015年的产量为a.则
2016年的增产量为 _______;实际产量为___________;
2017的增产量为__________;实际产量为___________;
列方程为___________________________________;
例2
利民大药房将原来每盒盈利30%的某种药品,先后两次降价,经两次降价后每盒仍能盈利10%,求这两次降价的平均降价率是多少?
分析:设某种药品进价是a元/盒,零售价按盈利30%定价
就是_________________元/盒,两次降价后仍能盈利10%,
就是_________________元/盒,设两次平均降价率是x,
则第一次降价后的零售价为___________________________,
第二次降价后的零售价为____________________________
列方程得:_____________.
归纳:
设基数为a,平均增长率为x,
则一次增长后的值为_____________;
二次增长后的值为_____________________;
依次类推n次增长后的值为_________________.
求降低率时,则是把“+”号改为“-”号。
四、巩固练习:(8分钟)
1.乐清花鸟市场去年一月份花苗销售额为60万元,二月份由于某种原因,销售额下降了10%,以后改进管理,增加品种数量,月销售额大幅上升,到四月份销售额猛增到96万元,求三、四月份平均每月增长的百分率是多少?(精确到0.1%)
2.某校为美化校园,逐年扩大校园绿化面积.据统计,今年的绿化面积是前年绿化面积的1.25倍,那么这两年平均每年校园绿化面积增加的百分率是多少(精确到1℅)?
提示:增长率问题中若基数不明确,通常可设为“1”,或设为a等。
五、课堂小结:(2分钟)
本节课,你学到了哪些知识?
1.列一元二次方程解应用题的基本步骤:
审 设 列 解 验 答
2.增长率(降低率)问题:
设基数为a,平均增长率为x,
a(1+x)n =n次增长后的值
a(1-x)n =n次降低后的值
六、布置作业:(8分钟) 讨论补充记
录
讨论补充记
录
一、学习目标: 四、巩固练习:
二、自学提纲: 五、课堂小结:
三、合作探究: 六、布置作业:
教 学 反 思
