沪科版八下:19.3.2 菱形 教案(表格式,2课时)
文档属性
| 名称 | 沪科版八下:19.3.2 菱形 教案(表格式,2课时) |  | |
| 格式 | doc | ||
| 文件大小 | 181.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 11:55:52 | ||
图片预览


文档简介
19.3.2菱形(1)
时间
地点
召集人
课题 19.3.2菱形 课时 第 1课时
(总第 1 课时) 科任教师
授课时间
教学 目标 知识与能力:1.掌握菱形的概念,知道菱形与平行四边形的关系。
2.理解并掌握菱形的定义及性质,会用这些性质进行有关的论证和计算,会计算菱形的面积。
过程与方法:通过课堂合作学习让学生自己完成例题,培养学生的探究能力。
情感态度价值观:培养学生勇于探索的思想意识。
重难点 重点:菱形的性质。
难点:菱形的性质及其综合应用。
教
学
过
程
教
学
过
程
一、导入新课、揭示目标(2分钟左右)
1.掌握菱形的概念,知道菱形与平行四边形的关系。
2.理解并掌握菱形的定义及性质,会用这些性质进行有关的论证和计算,会计算菱形的面积。
二、学生自学,质疑问难(10分钟左右)
自学提纲:
阅读课本内容,完成以下任务。
1.什么是菱形?它和平行四边形有什么关系?
2.画一个菱形,量一下它的四条边长,两条对角线的夹角的度数,你有什么发现?
3.菱形有哪些性质?请你一一说出。
4.你能证明这些性质吗?试试看,与你的同伴交流一下。
5.菱形的面积公式是什么?说说理由。
6.学习例5。
7.完成练习第1,2题。
8.已知:菱形ABCD的对角线AC和BD相交于点O,如图。
求证:AC⊥BD ; AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC 。
三、合作探究,解决疑难(15分钟左右)
1.动手操作:
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形纸片?
2.探索菱形的性质。
3.证明菱形的性质。
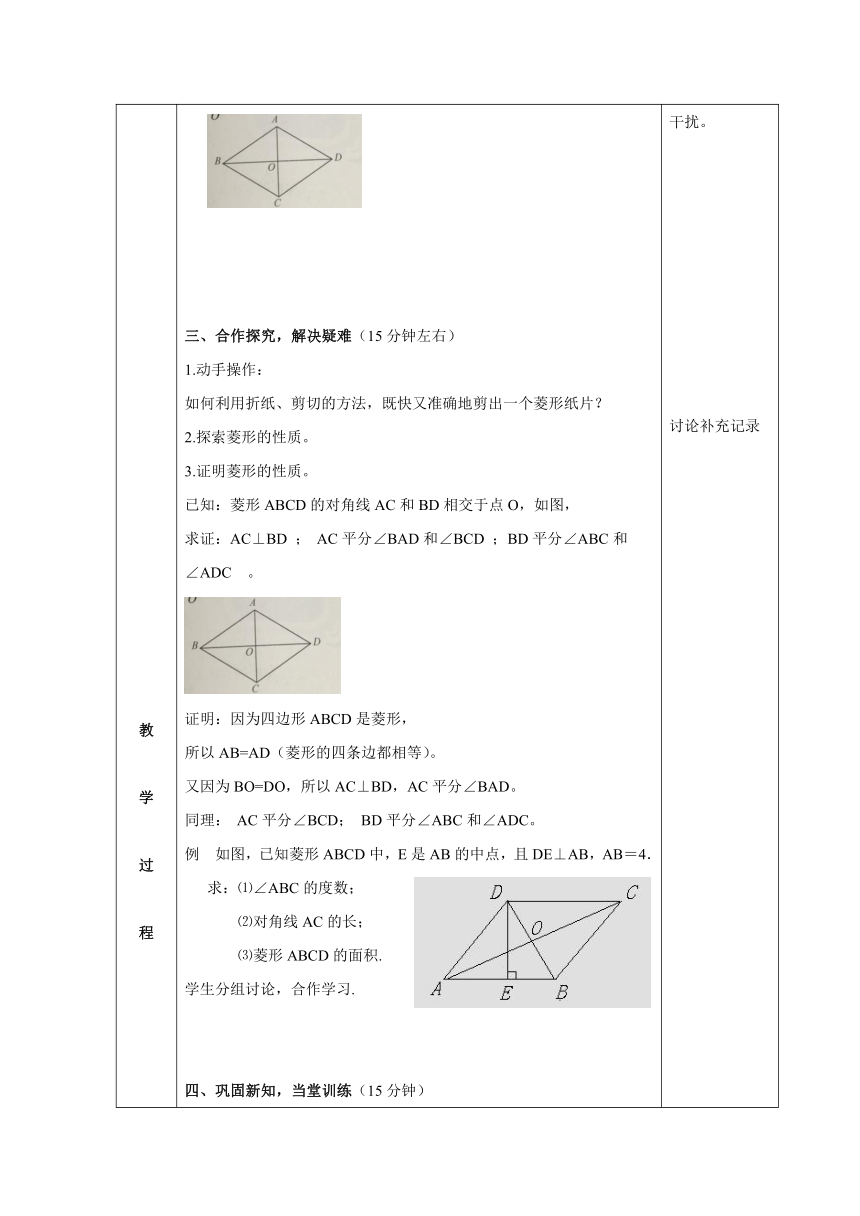
已知:菱形ABCD的对角线AC和BD相交于点O,如图,
求证:AC⊥BD ; AC平分∠BAD和∠BCD ;BD平分∠ABC和
∠ADC 。
证明:因为四边形ABCD是菱形,
所以AB=AD(菱形的四条边都相等)。
又因为BO=DO,所以AC⊥BD,AC平分∠BAD。
同理: AC平分∠BCD; BD平分∠ABC和∠ADC。
例 如图,已知菱形ABCD中,E是AB的中点,且DE⊥AB,AB=4.
求:⑴∠ABC的度数;
⑵对角线AC的长;
⑶菱形ABCD的面积.
学生分组讨论,合作学习.
四、巩固新知,当堂训练(15分钟)
1.已知菱形的周长是12cm,那么它的边长是______.
2.在菱形ABCD中,∠ABC=60°,则∠BAC=_______.
3.如图,在菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两条对角线AC、BD的长。
五、课堂小结
菱形的性质定理1:菱形的四条边都相等.
菱形的性质定理2:菱形的两条对角线互相垂直平分,每一条对角线平分一组对角。
六、布置作业,拓展延伸(3分钟) 讨论补充记录
学生自学。对不会的问题要做好批注或随笔,作为合作探究的问题进行合作探究。教师检查学情,不指导、不提问、不干扰。
讨论补充记录
板书 设计
教 学 反 思
19.3.2菱形(2)
主备人:
时间
地点
召集人
课题 19.3.2菱形 课时 第 2 课时
(总第 2 课时) 科任教师
授课时间
教学 目标 知识与能力:1.探索并掌握菱形的判定方法.
2.能说出菱形的两个判定定理,并会用它们进行相关的论证和计算.
过程与方法:经历探究菱形的判定条件的过程,通过操作、观察、猜想、证明的过程,培养学生的科学探索精神.
情感态度价值观:
1.让学生在探究过程中加深对菱形的理解,养成主动探索的学习习惯.
2.通过菱形与矩形的判定方法的类比,进一步体会类比的思想方法的作用.
重难点 重点:菱形的判定方法。
难点:探究菱形的判定条件并合理利用它们进行论证和计算。
教
学
过
程
教
学
过
程
一.复习提问:
什么叫菱形?
菱形有哪些性质?
答:菱形的两组对边平行,四条边相等;菱形的两组对角相等,邻角互补;
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角.
二.导入新课、揭示目标(2分钟左右)
1.探索并掌握菱形的判定方法.
2.能说出菱形的两个判定定理,并会用它们进行相关的论证和计算.
三.学生自学,质疑问难(10分钟左右)
自学提纲:
1.阅读课本内容,完成以下任务.
2.请你说说菱形的性质1的逆命题,猜想一下它是真命题吗?
3.画两条互相垂直的直线l1、l2,两直线交于点O,在l1取两点A,C,使OA=OC,在l2上取两点B,D,使OB=OD,顺次连接点A,B,C,D, 四边形ABCD是菱形吗?为什么?
4.菱形的判定方法有哪些?
5.你能证明这些判定方法吗?试试看,与你的同伴交流一下。
6.学习例6.
7.完成练习3,4两题 .
8.如图,ABCD的两条对角线AC、BD
相交于点O,AB=5,AC=8,DB=6.
(1)AC、BD互相垂直吗?为什么?
(2)四边形ABCD是菱形吗?为什么?
四、合作探究,解决疑难(15分钟左右)
1.探索菱形常用的判定方法:
探究活动一:
根据菱形的定义,可得菱形的第一个判定方法:
有一组邻边相等的平行四边形叫做菱形.
探究活动二:
2)对角线互相垂直的平行四边形是菱形.
探究活动三:
3)有四条边相等的四边形是菱形.
2.如图, ABCD的两条对角线AC、BD 相交于点O,AB=5,AC=8,DB=6.
(1)AC、BD互相垂直吗?为什么?
(2)四边形ABCD是菱形吗?为什么?
解:(1)因为四边形ABCD是平行四边形,所以OA=OC=4, OB=OD=3.
因为AB=5,AB2=OA2+OB2,
所以∠AOB=90°,所以AC⊥BD。
(2)因为四边形ABCD是平行四边形,AC⊥BD,所以四边形ABCD是菱形.
五、巩固新知,当堂训练(15分钟)
ABCD的对角线AC与BD相交于点O.
(1)若AB=AD,则ABCD是 形;
(2)若AC=BD,则ABCD是 形;
(3)若∠ABC是直角,则ABCD是 形;
(4)若∠BAO=∠DAO,则ABCD是 形。
六、课堂小结
这节课你有哪些收获?
七、布置作业,拓展延伸(3分钟) 讨论补充记录
学生自学。对不会的问题要做好批注或随笔,作为合作探究的问题进行合作探究。教师检查学情,不指导、不提问、不干扰。
讨论补充记录
板书 设计
教 学 反 思
时间
地点
召集人
课题 19.3.2菱形 课时 第 1课时
(总第 1 课时) 科任教师
授课时间
教学 目标 知识与能力:1.掌握菱形的概念,知道菱形与平行四边形的关系。
2.理解并掌握菱形的定义及性质,会用这些性质进行有关的论证和计算,会计算菱形的面积。
过程与方法:通过课堂合作学习让学生自己完成例题,培养学生的探究能力。
情感态度价值观:培养学生勇于探索的思想意识。
重难点 重点:菱形的性质。
难点:菱形的性质及其综合应用。
教
学
过
程
教
学
过
程
一、导入新课、揭示目标(2分钟左右)
1.掌握菱形的概念,知道菱形与平行四边形的关系。
2.理解并掌握菱形的定义及性质,会用这些性质进行有关的论证和计算,会计算菱形的面积。
二、学生自学,质疑问难(10分钟左右)
自学提纲:
阅读课本内容,完成以下任务。
1.什么是菱形?它和平行四边形有什么关系?
2.画一个菱形,量一下它的四条边长,两条对角线的夹角的度数,你有什么发现?
3.菱形有哪些性质?请你一一说出。
4.你能证明这些性质吗?试试看,与你的同伴交流一下。
5.菱形的面积公式是什么?说说理由。
6.学习例5。
7.完成练习第1,2题。
8.已知:菱形ABCD的对角线AC和BD相交于点O,如图。
求证:AC⊥BD ; AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC 。
三、合作探究,解决疑难(15分钟左右)
1.动手操作:
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形纸片?
2.探索菱形的性质。
3.证明菱形的性质。
已知:菱形ABCD的对角线AC和BD相交于点O,如图,
求证:AC⊥BD ; AC平分∠BAD和∠BCD ;BD平分∠ABC和
∠ADC 。
证明:因为四边形ABCD是菱形,
所以AB=AD(菱形的四条边都相等)。
又因为BO=DO,所以AC⊥BD,AC平分∠BAD。
同理: AC平分∠BCD; BD平分∠ABC和∠ADC。
例 如图,已知菱形ABCD中,E是AB的中点,且DE⊥AB,AB=4.
求:⑴∠ABC的度数;
⑵对角线AC的长;
⑶菱形ABCD的面积.
学生分组讨论,合作学习.
四、巩固新知,当堂训练(15分钟)
1.已知菱形的周长是12cm,那么它的边长是______.
2.在菱形ABCD中,∠ABC=60°,则∠BAC=_______.
3.如图,在菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两条对角线AC、BD的长。
五、课堂小结
菱形的性质定理1:菱形的四条边都相等.
菱形的性质定理2:菱形的两条对角线互相垂直平分,每一条对角线平分一组对角。
六、布置作业,拓展延伸(3分钟) 讨论补充记录
学生自学。对不会的问题要做好批注或随笔,作为合作探究的问题进行合作探究。教师检查学情,不指导、不提问、不干扰。
讨论补充记录
板书 设计
教 学 反 思
19.3.2菱形(2)
主备人:
时间
地点
召集人
课题 19.3.2菱形 课时 第 2 课时
(总第 2 课时) 科任教师
授课时间
教学 目标 知识与能力:1.探索并掌握菱形的判定方法.
2.能说出菱形的两个判定定理,并会用它们进行相关的论证和计算.
过程与方法:经历探究菱形的判定条件的过程,通过操作、观察、猜想、证明的过程,培养学生的科学探索精神.
情感态度价值观:
1.让学生在探究过程中加深对菱形的理解,养成主动探索的学习习惯.
2.通过菱形与矩形的判定方法的类比,进一步体会类比的思想方法的作用.
重难点 重点:菱形的判定方法。
难点:探究菱形的判定条件并合理利用它们进行论证和计算。
教
学
过
程
教
学
过
程
一.复习提问:
什么叫菱形?
菱形有哪些性质?
答:菱形的两组对边平行,四条边相等;菱形的两组对角相等,邻角互补;
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角.
二.导入新课、揭示目标(2分钟左右)
1.探索并掌握菱形的判定方法.
2.能说出菱形的两个判定定理,并会用它们进行相关的论证和计算.
三.学生自学,质疑问难(10分钟左右)
自学提纲:
1.阅读课本内容,完成以下任务.
2.请你说说菱形的性质1的逆命题,猜想一下它是真命题吗?
3.画两条互相垂直的直线l1、l2,两直线交于点O,在l1取两点A,C,使OA=OC,在l2上取两点B,D,使OB=OD,顺次连接点A,B,C,D, 四边形ABCD是菱形吗?为什么?
4.菱形的判定方法有哪些?
5.你能证明这些判定方法吗?试试看,与你的同伴交流一下。
6.学习例6.
7.完成练习3,4两题 .
8.如图,ABCD的两条对角线AC、BD
相交于点O,AB=5,AC=8,DB=6.
(1)AC、BD互相垂直吗?为什么?
(2)四边形ABCD是菱形吗?为什么?
四、合作探究,解决疑难(15分钟左右)
1.探索菱形常用的判定方法:
探究活动一:
根据菱形的定义,可得菱形的第一个判定方法:
有一组邻边相等的平行四边形叫做菱形.
探究活动二:
2)对角线互相垂直的平行四边形是菱形.
探究活动三:
3)有四条边相等的四边形是菱形.
2.如图, ABCD的两条对角线AC、BD 相交于点O,AB=5,AC=8,DB=6.
(1)AC、BD互相垂直吗?为什么?
(2)四边形ABCD是菱形吗?为什么?
解:(1)因为四边形ABCD是平行四边形,所以OA=OC=4, OB=OD=3.
因为AB=5,AB2=OA2+OB2,
所以∠AOB=90°,所以AC⊥BD。
(2)因为四边形ABCD是平行四边形,AC⊥BD,所以四边形ABCD是菱形.
五、巩固新知,当堂训练(15分钟)
ABCD的对角线AC与BD相交于点O.
(1)若AB=AD,则ABCD是 形;
(2)若AC=BD,则ABCD是 形;
(3)若∠ABC是直角,则ABCD是 形;
(4)若∠BAO=∠DAO,则ABCD是 形。
六、课堂小结
这节课你有哪些收获?
七、布置作业,拓展延伸(3分钟) 讨论补充记录
学生自学。对不会的问题要做好批注或随笔,作为合作探究的问题进行合作探究。教师检查学情,不指导、不提问、不干扰。
讨论补充记录
板书 设计
教 学 反 思
