人教版四年级上册《教材新解》 2 角的分类及画角 同步教材详解(含答案)
文档属性
| 名称 | 人教版四年级上册《教材新解》 2 角的分类及画角 同步教材详解(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 00:00:00 | ||
图片预览


文档简介
2 角的分类及画角(教材P42~46)
教材提示
目标导向
1.认识常见的几种角,并知道它们之间的关系。
2.会用量角器量指定度数画角。
3.培养规范的作图习惯。
重点导学
在认识角的基础上对角进行分类。
难点剖析
锐角、直角、钝角、平角、周角的关系: 锐角<直角<钝角<平角<周角。
直角、平角、周角的度数是固定不变的,1周角=2平角=4直角。
教材新解
教材讲解
知识点1 认识平角和周角
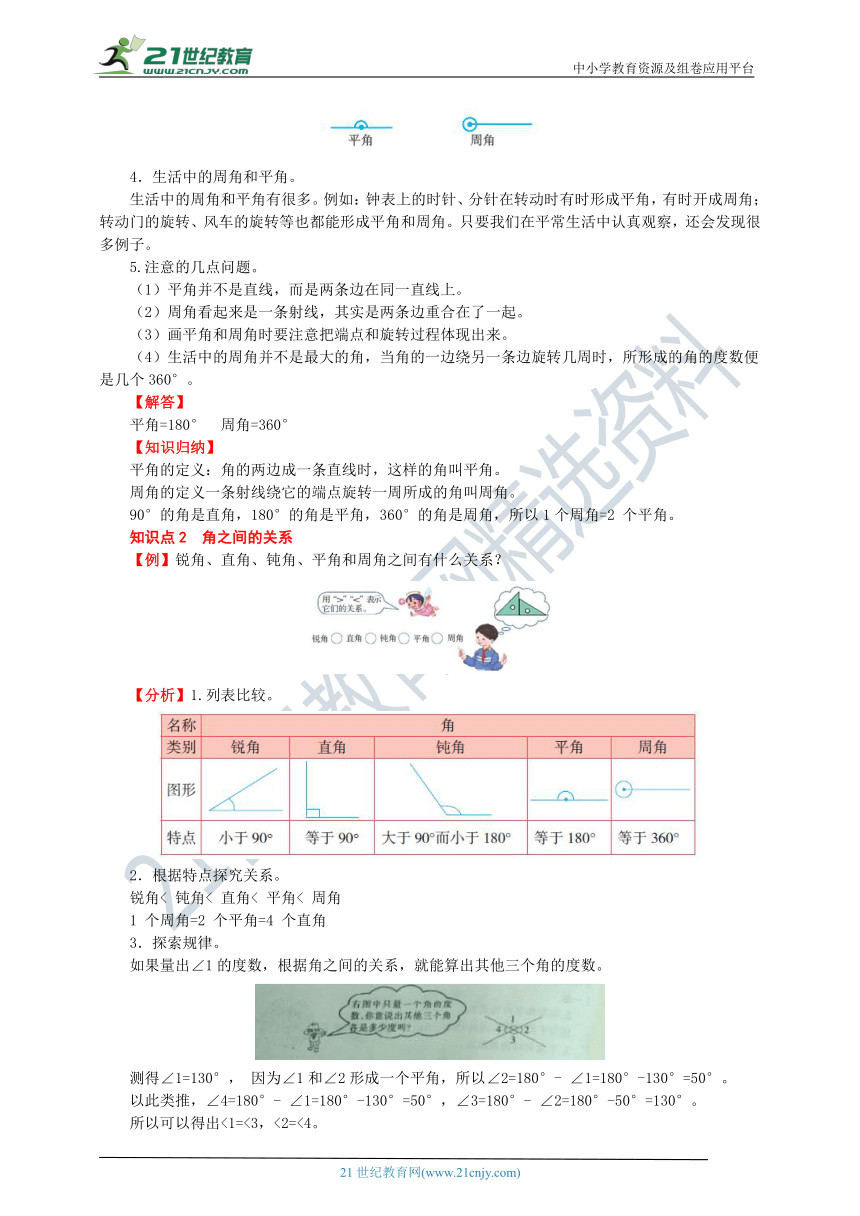
【例】三角尺上有一个角是直角,用量角器量一量,这个直角是多少度?
1直角=90°
角可以看作由一条射线绕着它的端点,从一个位置旋转到另一个位置所成的图形。
【分析】
1.平角和周角的概念。
角的两边成一条直线时,这样的角叫平角。注意明确:平角并不是一条直线,而是两条边在同一直线上。
平角=180°
一条射线绕它的端点旋转一周所成的角叫周角。
2.周角和平角的关系。
因为平角=180°,周角=360°,所以1 个周角=2 个平角。
平角和周角的画法。
4.生活中的周角和平角。
生活中的周角和平角有很多。例如:钟表上的时针、分针在转动时有时形成平角,有时开成周角;转动门的旋转、风车的旋转等也都能形成平角和周角。只要我们在平常生活中认真观察,还会发现很多例子。
5.注意的几点问题。
平角并不是直线,而是两条边在同一直线上。
周角看起来是一条射线,其实是两条边重合在了一起。
画平角和周角时要注意把端点和旋转过程体现出来。
(4)生活中的周角并不是最大的角,当角的一边绕另一条边旋转几周时,所形成的角的度数便是几个360°。
【解答】
平角=180° 周角=360°
【知识归纳】
平角的定义:角的两边成一条直线时,这样的角叫平角。
周角的定义一条射线绕它的端点旋转一周所成的角叫周角。
90°的角是直角,180°的角是平角,360°的角是周角,所以1个周角=2 个平角。
知识点2 角之间的关系
【例】锐角、直角、钝角、平角和周角之间有什么关系?
【分析】1.列表比较。
2.根据特点探究关系。
锐角< 钝角< 直角< 平角< 周角
1 个周角=2 个平角=4 个直角
3.探索规律。
如果量出∠1的度数,根据角之间的关系,就能算出其他三个角的度数。
测得∠1=130°, 因为∠1和∠2形成一个平角,所以∠2=180°- ∠1=180°-130°=50°。
以此类推,∠4=180°- ∠1=180°-130°=50°,∠3=180°- ∠2=180°-50°=130°。
所以可以得出<1=<3,<2=<4。
【解答】
锐角< 钝角< 直角< 平角< 周角
1 个周角=2 个平角=4 个直角
【知识归纳】
锐角< 钝角< 直角< 平角< 周角;1 个周角=2 个平角=4 个直角;两条直线相交所
形成的四个角中,对顶角相等。
【例】读出下面各数。
知识点3 画角的方法
【例】:画一个60°的角。
【分析】1.画角的步骤。
(1)画一条射线,使量角器的中心和射线的端点重合,0° 刻度线和射线重合。
(2)在量角器60° 刻度线的地方点一个点。
(3)以画出的射线的端点为端点,通过刚画的点,再画一条射线。
2.画大于180°的任意角。
根据平角和周角的度数也可以大于180° 的任意角。如画210° 的角,可以先画一个平角,在此基础上画一个“30°”的角,合起来便是210° 的角(如左下图),也可以画一个360°-210°=150° 的角,150° 角所对的外角便是210° 的角(如右下图)。
【知识归纳】
画指定度数的角,要注意做到:“两重合”:量角器的中心与顶点重合,“0 刻度线与所画的一条边重合;还要看准度数,所画的边对应的0 刻度在内圈,看的就是内圈刻度;所画的边对应的0 刻度在外圈,看的就是外圈刻度。
误区点拨
【误区1】判断:钝角就是大于90°的角。( )
错误解答:√
误区分析:这种理解错在对钝角的特征认识不到位,钝角是大于90°而小于180°的角。
正确解答:×
提示:钝角是大于90°而小于180°的角。要注意的是钝角一定大于90°,但大于90°的角不一定是钝角。
【误区2】判断:只有用量角器才能画角。( )
错误解答:√
误区分析:此题对画角的方法理解错误。
正确解答:×
提示:画角的方法一定要掌握灵活,一些特殊的角可以借用三角尺或直尺来画。不是所有的角都一定要用量角器去画,有一些角借助三角板画更简便。如15°、30°、45°、60°、75°、90°、105°、120°、135°、150°的角都可以用三角尺画出。
【误区3】量出下面各角的度数,并说出各是哪一种角?
错误解答:∠1是直角,∠2是钝角,∠3是锐角。
误区分析:此题对锐角和钝角的认识有错误。运用量角器度量后可知:∠1=90°,∠2=45°,∠3=150°我们已经学习过90°的角是直角,大于0°小于90°的角叫做锐角,大于90°小于180°的角叫做钝角。由于0°<∠2<90°,90°<3<180°,因而可知,∠1是直角,∠2 是锐角,∠3是钝角。
正确解答:∠1是直角,∠2是锐角,∠3是钝角。
提示:明确小于90°的角叫做锐角; 等于90°的角叫做直角;大于90°的角叫做钝角。
典型剖析
【例1】说说每个钟面上时针和分针组成的是什么角?
【思路点拨】看时针和分针组成的角的大小,如果比直角小就是锐角,如果比直角大但时针和分针不在同一直线上就叫钝角。如果分针和时针在同一直线上但没有重合,所组成的角叫平角。如果时针和分针旋转至重合,所组成的角叫周角。
【解答】(1)锐角 (2)直角 (3)周角 (4)钝角
【知识归纳】
本题主要考查对各种角的认识,小于90°的是锐角,等于90°的是直角,大于90°而小于180°的是钝角,等于180°的是平角,周角是360°。由此就不难得出结论了。
【例2】用量角器画一个65°的角。
【思路点拨】1.画一条射线。
2.确定角度。
使量角器的中心和射线的端点重合,0刻度线和射线重合。在量角器65°刻线处点一个点。
3.确定角的另一条边 以画出的射线的端点为端点,通过刚画的点,再画一条射线。
4.标好角的符号及度数 (如上图)。
【解答】步骤:①画一条射线,使量角器的中心和射线的端点重合,0刻度线和射线重合。②在量角器65°刻度线的地方点一个点。③以画出的射线的端点为端点,通过刚画好的点,再画一条射线。
【知识归纳】
画指定度数的角,要注意做到“两重合”;量角器的中心与角的顶点重合,0刻度线与所画的一条边重合;还要看准度数,所画的边对应的0刻度在内圈,看的就是内圈刻度;所画的边对应的0刻度的外圈,看的就是外圈刻度。
【例3】下面两个图中的∠1和∠2是不是相等?为什么?
【思路点拨】(1)因为∠1=90°-∠3,∠2=90°-∠3,所以∠1=∠2。
(2)因为∠1=180°-∠3,∠2=180°-∠3,所以∠1=∠2。
【解答】(1)∠1=∠2 (2)∠1=∠2
【知识归纳】
本题主要考查对角的大小计算这一知识点。
推铅球出手仰角应该是45°吗?
想一想:推铅球要推得远,出手的仰角应采用45°吗?还是较45°小些或大些?许多教科书中,都讨论过样的问题:
设一抛体以一定的速率斜向抛射,如果空气阻力可以忽略,则它落回同一水平时,其水平距离以仰角为45°时为最大。
但是,推铅球的抛掷点不是在地面上,而是离地一段高度h,如图所示。图中表示,以同一出手速率作45°及40°仰角抛掷,当落回抛掷点同一水平时,水平距离以45°者较大。但是,当它们落到地面时,水平距离却以40°者较大。
通过复杂的计算,获得以下的结论:扒铅球欲得最大的距离,其出手的爷角应小于45°,这角度随出手速度的增大而增大,而随出手高度的增大而减小。对出手高度为1.7米~2米,而出手速度为8~14米/秒的人来,出手仰角应为38°~42°。准确数字可从体育理论中由曲线查得。
至于其它掷类,受空气的作用力影响较大,各有不同的最佳仰角。例如掷铁饼为30°~35°;标枪为28°~33°;链球为42°~44°
第三单元小结
具体内容
重点知识
认识线段、直线、射线
线段有两个端点,直线没有端点。可以向两端无限延伸;射线只有一个端点,可以向一端无限延伸。
线段和射线都是直线的一部分,射线和直线都无法测量出长度。
角的认识
从一点引出两条射线所组成的图形叫做角,用符号“∠”。
把量角器放在角的上面。便量角器的中心和角的顶点重合,零刻度线和角的一条边重合。
用量角器量角、画角时,确定好使用内、外圈刻度是关键。
角的大小
角的大小与两条边的长短无关,与两边张开的大小有关,张开得越大,角越大。
角的分类
小于90°的角叫做锐角;等于90°的角叫做直角,大于90°的角叫做钝角。角的两边成一条直线时,这样的角叫平角,平角=180°,一条射线绕它的端点旋转一周所成的角叫周角,周角=360°,一个周角 =两个平角。
画角的方法
画指定度数的角,要注意做到“两重合”量角器的中心与顶点重合,“0”刻度线与所画的一条边重合,还要看准度数,所画的边对应的0刻度在内圈,看的就是内圈刻度,所画的边对应的0刻度在外圈,看的就是外圈刻度。
教材提示
目标导向
1.认识常见的几种角,并知道它们之间的关系。
2.会用量角器量指定度数画角。
3.培养规范的作图习惯。
重点导学
在认识角的基础上对角进行分类。
难点剖析
锐角、直角、钝角、平角、周角的关系: 锐角<直角<钝角<平角<周角。
直角、平角、周角的度数是固定不变的,1周角=2平角=4直角。
教材新解
教材讲解
知识点1 认识平角和周角
【例】三角尺上有一个角是直角,用量角器量一量,这个直角是多少度?
1直角=90°
角可以看作由一条射线绕着它的端点,从一个位置旋转到另一个位置所成的图形。
【分析】
1.平角和周角的概念。
角的两边成一条直线时,这样的角叫平角。注意明确:平角并不是一条直线,而是两条边在同一直线上。
平角=180°
一条射线绕它的端点旋转一周所成的角叫周角。
2.周角和平角的关系。
因为平角=180°,周角=360°,所以1 个周角=2 个平角。
平角和周角的画法。
4.生活中的周角和平角。
生活中的周角和平角有很多。例如:钟表上的时针、分针在转动时有时形成平角,有时开成周角;转动门的旋转、风车的旋转等也都能形成平角和周角。只要我们在平常生活中认真观察,还会发现很多例子。
5.注意的几点问题。
平角并不是直线,而是两条边在同一直线上。
周角看起来是一条射线,其实是两条边重合在了一起。
画平角和周角时要注意把端点和旋转过程体现出来。
(4)生活中的周角并不是最大的角,当角的一边绕另一条边旋转几周时,所形成的角的度数便是几个360°。
【解答】
平角=180° 周角=360°
【知识归纳】
平角的定义:角的两边成一条直线时,这样的角叫平角。
周角的定义一条射线绕它的端点旋转一周所成的角叫周角。
90°的角是直角,180°的角是平角,360°的角是周角,所以1个周角=2 个平角。
知识点2 角之间的关系
【例】锐角、直角、钝角、平角和周角之间有什么关系?
【分析】1.列表比较。
2.根据特点探究关系。
锐角< 钝角< 直角< 平角< 周角
1 个周角=2 个平角=4 个直角
3.探索规律。
如果量出∠1的度数,根据角之间的关系,就能算出其他三个角的度数。
测得∠1=130°, 因为∠1和∠2形成一个平角,所以∠2=180°- ∠1=180°-130°=50°。
以此类推,∠4=180°- ∠1=180°-130°=50°,∠3=180°- ∠2=180°-50°=130°。
所以可以得出<1=<3,<2=<4。
【解答】
锐角< 钝角< 直角< 平角< 周角
1 个周角=2 个平角=4 个直角
【知识归纳】
锐角< 钝角< 直角< 平角< 周角;1 个周角=2 个平角=4 个直角;两条直线相交所
形成的四个角中,对顶角相等。
【例】读出下面各数。
知识点3 画角的方法
【例】:画一个60°的角。
【分析】1.画角的步骤。
(1)画一条射线,使量角器的中心和射线的端点重合,0° 刻度线和射线重合。
(2)在量角器60° 刻度线的地方点一个点。
(3)以画出的射线的端点为端点,通过刚画的点,再画一条射线。
2.画大于180°的任意角。
根据平角和周角的度数也可以大于180° 的任意角。如画210° 的角,可以先画一个平角,在此基础上画一个“30°”的角,合起来便是210° 的角(如左下图),也可以画一个360°-210°=150° 的角,150° 角所对的外角便是210° 的角(如右下图)。
【知识归纳】
画指定度数的角,要注意做到:“两重合”:量角器的中心与顶点重合,“0 刻度线与所画的一条边重合;还要看准度数,所画的边对应的0 刻度在内圈,看的就是内圈刻度;所画的边对应的0 刻度在外圈,看的就是外圈刻度。
误区点拨
【误区1】判断:钝角就是大于90°的角。( )
错误解答:√
误区分析:这种理解错在对钝角的特征认识不到位,钝角是大于90°而小于180°的角。
正确解答:×
提示:钝角是大于90°而小于180°的角。要注意的是钝角一定大于90°,但大于90°的角不一定是钝角。
【误区2】判断:只有用量角器才能画角。( )
错误解答:√
误区分析:此题对画角的方法理解错误。
正确解答:×
提示:画角的方法一定要掌握灵活,一些特殊的角可以借用三角尺或直尺来画。不是所有的角都一定要用量角器去画,有一些角借助三角板画更简便。如15°、30°、45°、60°、75°、90°、105°、120°、135°、150°的角都可以用三角尺画出。
【误区3】量出下面各角的度数,并说出各是哪一种角?
错误解答:∠1是直角,∠2是钝角,∠3是锐角。
误区分析:此题对锐角和钝角的认识有错误。运用量角器度量后可知:∠1=90°,∠2=45°,∠3=150°我们已经学习过90°的角是直角,大于0°小于90°的角叫做锐角,大于90°小于180°的角叫做钝角。由于0°<∠2<90°,90°<3<180°,因而可知,∠1是直角,∠2 是锐角,∠3是钝角。
正确解答:∠1是直角,∠2是锐角,∠3是钝角。
提示:明确小于90°的角叫做锐角; 等于90°的角叫做直角;大于90°的角叫做钝角。
典型剖析
【例1】说说每个钟面上时针和分针组成的是什么角?
【思路点拨】看时针和分针组成的角的大小,如果比直角小就是锐角,如果比直角大但时针和分针不在同一直线上就叫钝角。如果分针和时针在同一直线上但没有重合,所组成的角叫平角。如果时针和分针旋转至重合,所组成的角叫周角。
【解答】(1)锐角 (2)直角 (3)周角 (4)钝角
【知识归纳】
本题主要考查对各种角的认识,小于90°的是锐角,等于90°的是直角,大于90°而小于180°的是钝角,等于180°的是平角,周角是360°。由此就不难得出结论了。
【例2】用量角器画一个65°的角。
【思路点拨】1.画一条射线。
2.确定角度。
使量角器的中心和射线的端点重合,0刻度线和射线重合。在量角器65°刻线处点一个点。
3.确定角的另一条边 以画出的射线的端点为端点,通过刚画的点,再画一条射线。
4.标好角的符号及度数 (如上图)。
【解答】步骤:①画一条射线,使量角器的中心和射线的端点重合,0刻度线和射线重合。②在量角器65°刻度线的地方点一个点。③以画出的射线的端点为端点,通过刚画好的点,再画一条射线。
【知识归纳】
画指定度数的角,要注意做到“两重合”;量角器的中心与角的顶点重合,0刻度线与所画的一条边重合;还要看准度数,所画的边对应的0刻度在内圈,看的就是内圈刻度;所画的边对应的0刻度的外圈,看的就是外圈刻度。
【例3】下面两个图中的∠1和∠2是不是相等?为什么?
【思路点拨】(1)因为∠1=90°-∠3,∠2=90°-∠3,所以∠1=∠2。
(2)因为∠1=180°-∠3,∠2=180°-∠3,所以∠1=∠2。
【解答】(1)∠1=∠2 (2)∠1=∠2
【知识归纳】
本题主要考查对角的大小计算这一知识点。
推铅球出手仰角应该是45°吗?
想一想:推铅球要推得远,出手的仰角应采用45°吗?还是较45°小些或大些?许多教科书中,都讨论过样的问题:
设一抛体以一定的速率斜向抛射,如果空气阻力可以忽略,则它落回同一水平时,其水平距离以仰角为45°时为最大。
但是,推铅球的抛掷点不是在地面上,而是离地一段高度h,如图所示。图中表示,以同一出手速率作45°及40°仰角抛掷,当落回抛掷点同一水平时,水平距离以45°者较大。但是,当它们落到地面时,水平距离却以40°者较大。
通过复杂的计算,获得以下的结论:扒铅球欲得最大的距离,其出手的爷角应小于45°,这角度随出手速度的增大而增大,而随出手高度的增大而减小。对出手高度为1.7米~2米,而出手速度为8~14米/秒的人来,出手仰角应为38°~42°。准确数字可从体育理论中由曲线查得。
至于其它掷类,受空气的作用力影响较大,各有不同的最佳仰角。例如掷铁饼为30°~35°;标枪为28°~33°;链球为42°~44°
第三单元小结
具体内容
重点知识
认识线段、直线、射线
线段有两个端点,直线没有端点。可以向两端无限延伸;射线只有一个端点,可以向一端无限延伸。
线段和射线都是直线的一部分,射线和直线都无法测量出长度。
角的认识
从一点引出两条射线所组成的图形叫做角,用符号“∠”。
把量角器放在角的上面。便量角器的中心和角的顶点重合,零刻度线和角的一条边重合。
用量角器量角、画角时,确定好使用内、外圈刻度是关键。
角的大小
角的大小与两条边的长短无关,与两边张开的大小有关,张开得越大,角越大。
角的分类
小于90°的角叫做锐角;等于90°的角叫做直角,大于90°的角叫做钝角。角的两边成一条直线时,这样的角叫平角,平角=180°,一条射线绕它的端点旋转一周所成的角叫周角,周角=360°,一个周角 =两个平角。
画角的方法
画指定度数的角,要注意做到“两重合”量角器的中心与顶点重合,“0”刻度线与所画的一条边重合,还要看准度数,所画的边对应的0刻度在内圈,看的就是内圈刻度,所画的边对应的0刻度在外圈,看的就是外圈刻度。
