人教版三年级上册数学《教材新解》 2 笔算乘法 2.1 多位数乘一位数(不进位) 同步教材详解(Word版有答案)
文档属性
| 名称 | 人教版三年级上册数学《教材新解》 2 笔算乘法 2.1 多位数乘一位数(不进位) 同步教材详解(Word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 19:34:27 | ||
图片预览

文档简介
2 笔算乘法(教材P60~76)
2.1 多位数乘一位数(不进位)(教材P60)
教材提示
目标导向
1.掌握多位数乘一位数(不进位)的计算方法,并能正确进行笔算。
2.能运用所学知识解决日常生活中的实际问题。
感受计算活动的现实意义,获得数学学习的成功体验。
重点导学
掌握多位数乘一位数(不进位)的笔算方法。
难点剖析
理解竖式计算的算理。
多位数乘一位数(不进位)的笔算方法:把多位数写在上面,一位数写在个位的下面,从个位乘起,用一位依次乘多位数每一位的数,与哪一位的数相乘得到的积就对应写在哪一位的下面。
教材新解
教材讲解
知识点 多位数乘一位数(不进位)的笔算方法
【例】怎样算一共有多少支彩笔?
【分析】1.理解题意。
通过观察图片,我们知道每盒彩笔有12支,3盒表示有3个12支,求一共有多少支,就是求3个12 是多少,用乘法计算,列式为12×3。
计算方法。
方法一:用加法计算。
12+12+12=36(支)
方法二:口算方法。
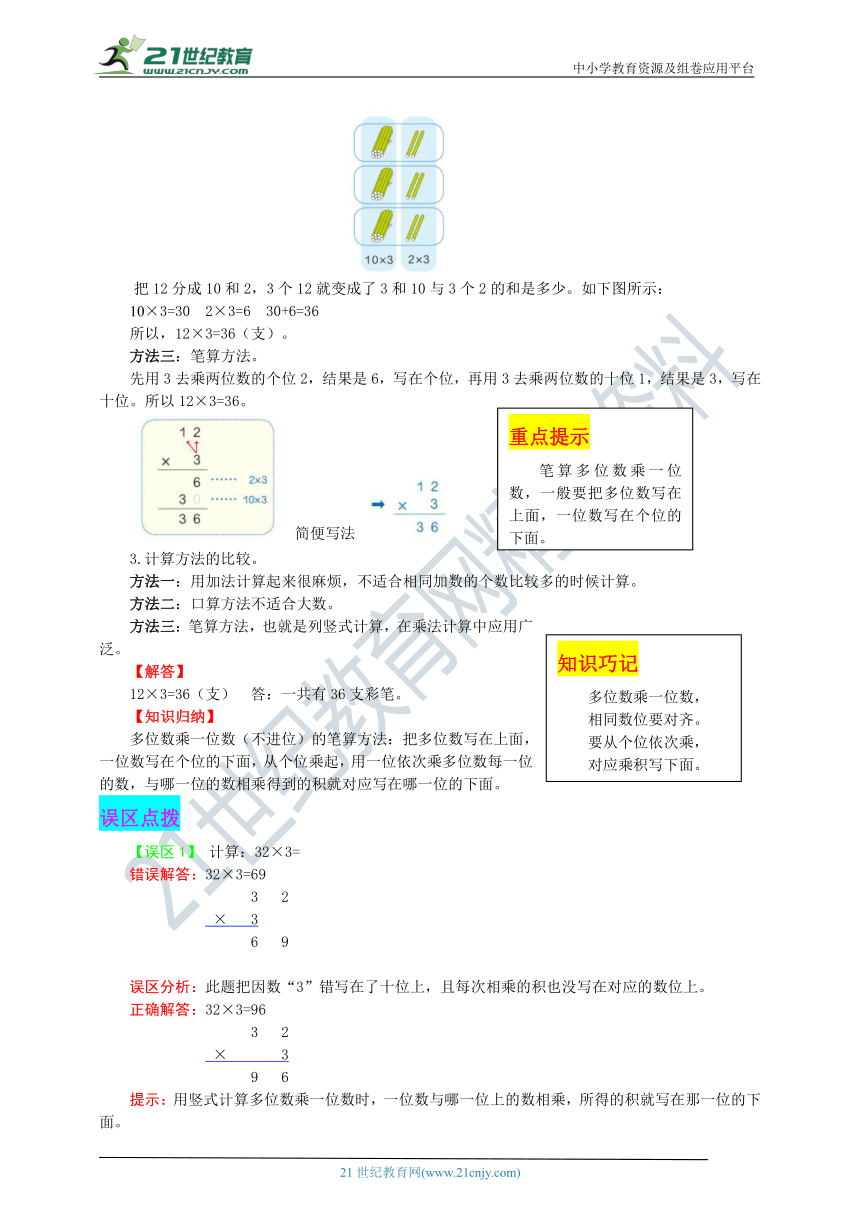
把12分成10和2,3个12就变成了3和10与3个2的和是多少。如下图所示:
10×3=30 2×3=6 30+6=36
所以,12×3=36(支)。
方法三:笔算方法。
先用3去乘两位数的个位2,结果是6,写在个位,再用3去乘两位数的十位1,结果是3,写在十位。所以12×3=36。
简便写法
计算方法的比较。
方法一:用加法计算起来很麻烦,不适合相同加数的个数比较多的时候计算。
方法二:口算方法不适合大数。
方法三:笔算方法,也就是列竖式计算,在乘法计算中应用广泛。
【解答】
12×3=36(支) 答:一共有36支彩笔。
【知识归纳】
多位数乘一位数(不进位)的笔算方法:把多位数写在上面,一位数写在个位的下面,从个位乘起,用一位依次乘多位数每一位的数,与哪一位的数相乘得到的积就对应写在哪一位的下面。
误区点拨
【误区1】 计算:32×3=
错误解答:32×3=69
3 2
× 3
6 9
误区分析:此题把因数“3”错写在了十位上,且每次相乘的积也没写在对应的数位上。
正确解答:32×3=96
3 2
× 3
9 6
提示:用竖式计算多位数乘一位数时,一位数与哪一位上的数相乘,所得的积就写在那一位的下面。
典型剖析
【例1】果园里有梨树122棵,杏树的棵树是梨树的4倍,果园里有杏树多少棵?
【思路点拨】我们可以借助线段图分析梨树与杏树之间的数量关系:
梨树: 122棵
杏树: 杏树?棵
杏树是梨树的3倍
由线段图可得,可以先求出杏树的棵树,再用梨树的棵树加上杏树的棵树。两种树的总棵树正好是梨树的(1+3)倍,因此也可以利用倍数关系求出总棵树。
1.根据较大的计数单位里面包含多少个较小的计数单位来判断进率。例如:“十”和“万”
【解答】方法一:122×3=366(棵) 366+122=488(棵)
方法二:1+3=4 122×4=488(棵)
【知识归纳】
解答和倍问题的关键在于找准1倍数,然后根据已知条件和所求问题,画出线段图,借助线段图解题。
史前期的算题
考古学家在西班牙发现了一处史前期壁画,上面除绘着一些人形和野兽的图形外,还绘着一些莫明其妙的算题,这些算题也是阿拉伯数字,但考古学家们看了半天,怎么也弄不明白这些算题。后来他们恍然大悟,原来这些算题中的数字与我们现在的数字并不是一回事,但是绝对符合四则运算的法则。小朋友,请你们仔细看看这些算式,想一想算式中的数字各等于现在的什么数字,然后把它翻译出来。
5+6+7=5×6×7
5+5=6
6÷5=6
7×5=7
2.1 多位数乘一位数(不进位)(教材P60)
教材提示
目标导向
1.掌握多位数乘一位数(不进位)的计算方法,并能正确进行笔算。
2.能运用所学知识解决日常生活中的实际问题。
感受计算活动的现实意义,获得数学学习的成功体验。
重点导学
掌握多位数乘一位数(不进位)的笔算方法。
难点剖析
理解竖式计算的算理。
多位数乘一位数(不进位)的笔算方法:把多位数写在上面,一位数写在个位的下面,从个位乘起,用一位依次乘多位数每一位的数,与哪一位的数相乘得到的积就对应写在哪一位的下面。
教材新解
教材讲解
知识点 多位数乘一位数(不进位)的笔算方法
【例】怎样算一共有多少支彩笔?
【分析】1.理解题意。
通过观察图片,我们知道每盒彩笔有12支,3盒表示有3个12支,求一共有多少支,就是求3个12 是多少,用乘法计算,列式为12×3。
计算方法。
方法一:用加法计算。
12+12+12=36(支)
方法二:口算方法。
把12分成10和2,3个12就变成了3和10与3个2的和是多少。如下图所示:
10×3=30 2×3=6 30+6=36
所以,12×3=36(支)。
方法三:笔算方法。
先用3去乘两位数的个位2,结果是6,写在个位,再用3去乘两位数的十位1,结果是3,写在十位。所以12×3=36。
简便写法
计算方法的比较。
方法一:用加法计算起来很麻烦,不适合相同加数的个数比较多的时候计算。
方法二:口算方法不适合大数。
方法三:笔算方法,也就是列竖式计算,在乘法计算中应用广泛。
【解答】
12×3=36(支) 答:一共有36支彩笔。
【知识归纳】
多位数乘一位数(不进位)的笔算方法:把多位数写在上面,一位数写在个位的下面,从个位乘起,用一位依次乘多位数每一位的数,与哪一位的数相乘得到的积就对应写在哪一位的下面。
误区点拨
【误区1】 计算:32×3=
错误解答:32×3=69
3 2
× 3
6 9
误区分析:此题把因数“3”错写在了十位上,且每次相乘的积也没写在对应的数位上。
正确解答:32×3=96
3 2
× 3
9 6
提示:用竖式计算多位数乘一位数时,一位数与哪一位上的数相乘,所得的积就写在那一位的下面。
典型剖析
【例1】果园里有梨树122棵,杏树的棵树是梨树的4倍,果园里有杏树多少棵?
【思路点拨】我们可以借助线段图分析梨树与杏树之间的数量关系:
梨树: 122棵
杏树: 杏树?棵
杏树是梨树的3倍
由线段图可得,可以先求出杏树的棵树,再用梨树的棵树加上杏树的棵树。两种树的总棵树正好是梨树的(1+3)倍,因此也可以利用倍数关系求出总棵树。
1.根据较大的计数单位里面包含多少个较小的计数单位来判断进率。例如:“十”和“万”
【解答】方法一:122×3=366(棵) 366+122=488(棵)
方法二:1+3=4 122×4=488(棵)
【知识归纳】
解答和倍问题的关键在于找准1倍数,然后根据已知条件和所求问题,画出线段图,借助线段图解题。
史前期的算题
考古学家在西班牙发现了一处史前期壁画,上面除绘着一些人形和野兽的图形外,还绘着一些莫明其妙的算题,这些算题也是阿拉伯数字,但考古学家们看了半天,怎么也弄不明白这些算题。后来他们恍然大悟,原来这些算题中的数字与我们现在的数字并不是一回事,但是绝对符合四则运算的法则。小朋友,请你们仔细看看这些算式,想一想算式中的数字各等于现在的什么数字,然后把它翻译出来。
5+6+7=5×6×7
5+5=6
6÷5=6
7×5=7
