人教版三年级上册数学《教材新解》 3 分数的简单应用 同步教材详解(Word版有答案)
文档属性
| 名称 | 人教版三年级上册数学《教材新解》 3 分数的简单应用 同步教材详解(Word版有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 00:00:00 | ||
图片预览



文档简介
3 分数的简单应用(教材P100~103)
教材提示
目标导向
1.会用分数表示阴影部分的面积。
2.理解简单的有关分数的应用题,初步了解分数的乘除法计算。
重点导学
用分数表示阴影部分的面积。
难点剖析
了解分数的乘除法计算。
教材新解
教材讲解
知识点1 用分数表示阴影的面积。
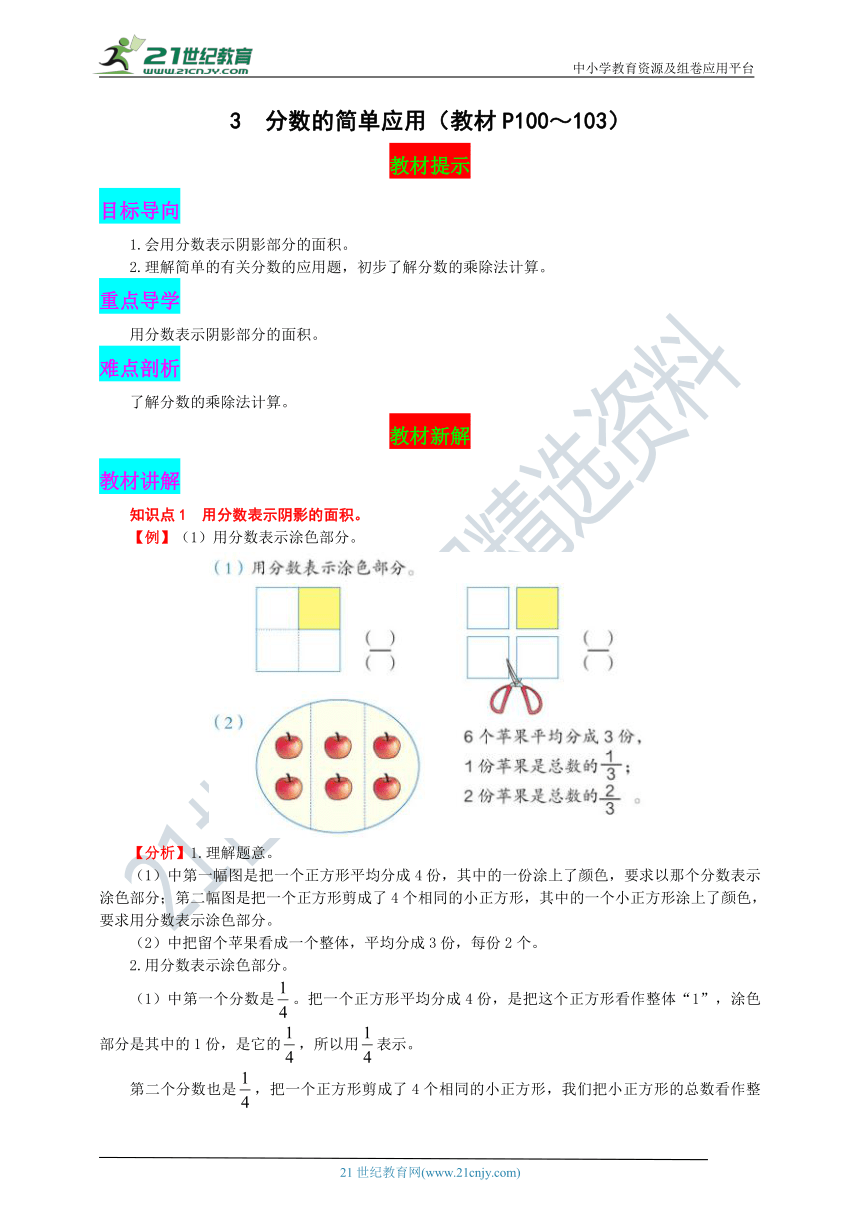
【例】(1)用分数表示涂色部分。
【分析】1.理解题意。
中第一幅图是把一个正方形平均分成4份,其中的一份涂上了颜色,要求以那个分数表示涂色部分;第二幅图是把一个正方形剪成了4个相同的小正方形,其中的一个小正方形涂上了颜色,要求用分数表示涂色部分。
中把留个苹果看成一个整体,平均分成3份,每份2个。
2.用分数表示涂色部分。
中第一个分数是。把一个正方形平均分成4份,是把这个正方形看作整体“1”,涂色部分是其中的1份,是它的,所以用表示。
第二个分数也是,把一个正方形剪成了4个相同的小正方形,我们把小正方形的总数看作整体“1”,即把整体“1”平均分成4份,涂色部分占了一份,是它的,所以用表示。
(2)6个苹果平均分成3份,这里把苹果总数圈起来,看作一个整体“1”,即把整体“1”平均分成3份,分母是3,1份是苹果总数的,2份是苹果总数的,3份是苹果总数的。
【解答】
(1)
【知识归纳】
我们既可以把一个完整的图形可以看作整体“1”,也可以把由多个个体组合在一起的图形或者物体看作整体“1”,用分数表示由多个个体组成的整体中的1份或几份时,整体份数就是这个分数的分母,其中,要表示的一份或几份就是这个分数的分子。
知识点2 求一个数的几分之几是多少
【例】有12名学生,其中是女生,是男生。男女生各有多少人?
【分析】1.理解题意。
12名学生是总数,是女生,是男生,是说明12名学生看成一个整体,把这个整体平均分成3份,女生占其中的一份,男生占2份。求男女生各有多少人,就是求着1份和2份各是多少。如下图所示:
女生是,就是把总人数12平均分成3份,求出1份的人数。用除法计算,12÷3=4(人)。
男生是,就是把总人数12平均分成3份,求出2份的人数。用除法计算,12÷3=4(人),4×2=8(人)。
我们还可以用总人数减去女生的人数就是男生的人数。12-4=8(人)。
【解答】
12÷3=4(人)
4×2=8(人)
答:女生有4人,男生有8人。
【知识归纳】
求一个数的几分之几是多少,就是用这个数除以分母,求出一份是多少,再用商乘分子。
误区点拨
【误区1】用分数表示下图中的阴影部分
错误解答:
误区分析:此题错在没有平均分。
正确解答:
提示:如果在图中画几条虚线,如图,便可看出阴影部分占这个长方形的,将图二右上角的阴影部分移至左下角,与左下角圆的合在一起变成整个正方形的。
【误区2】判断:数学兴趣小组有7名男生、3名女生,女生人数占数学兴趣小组的。( )
错误解答:√
误区分析:此题错把男生人数当做了整体,题中数学兴趣小组总人数是7+3=10(人)。女生应该占。
正确解答:×
提示:用分数表示时,不要混淆了整体和部分。
典型剖析
【例1】如下图涂红色的部分占整个图形的( );涂蓝色的部分占整个图形的( ); 涂蓝色的部分比涂红色部分多占( )。
【思路点拨】整个图形被平均分成了9份,每份就是,涂红色部分占了其中的4 份,是4个,涂蓝色部分占了其中的5分,是5个,用蓝色部分减红色部分时,根据同分母分数相加减,分母不变,分子相加减。
【解答】红色部分占整个图形的,蓝色部分占整个图形的,蓝色部分比红色部分多占 -= 。
【知识归纳】
用分数表示由多个个体组成的整体中的1份或几份时,整体份数就是这个分数的分母,其中,要表示的一份或几份就是这个分数的分子。
【例2】图中阴影部分占整个图形的几分之几?
【思路点拨】用割补法改变阴影部分的形状。
如图: 因此,阴影部分占整个图形的。
【解答】
【知识归纳】
用分数表示阴影部分的面积时,我们可以先采用割补法改变阴影部分的形状,然后再表示。
【例3】30个苹果的、各是多少?
【思路点拨】把30个苹果看成一个整体,求它的,也就是求把30个苹果平均分成6份,其中的5份是多少,列式为30÷6×5=25(个)。求它的,也就是求把30个苹果平均分成5份,其中的3份是多少,列式为30÷5×3=18(个)。
【解答】30÷6×5=25(个)
30÷5×3=18(个)
答:30个苹果的是25个,是18个。
【知识归纳】
分数的分子不是1时,表示的份数不是其中一份的数量,分子是几,表示的就是其中几份的数量。
分数小故事
一天,妈妈在市场上买回5块大小不同的饼,要平均分给爸爸、妈妈、姥爷、姥姥和我。妈妈问我:“怎么才能平均每人分到的份数一样多?”这下可难住我了。
就在这个时候,我突然想起来,原来杨老师教我们的:如果有6个人,每人分到几个的问题,于是,我对妈妈说:“一共有5个人,先把最大的饼平均分成五分之一,再把第二大的饼平均分成五分之一,然后把第三大的饼平均分成五分之一,接着把第四大的饼平均分成五分之一,最后把最小的饼平均分成五分之一,这样每个人从这五个饼中分别都取五分之一,加到一块,得到的饼一就样多了”。妈妈夸我真聪明,吃饼的时候还多给我一块呢。
今天我真高兴!
第八单元小结
具体内容
重点知识
分数的初步认识
几分之一:把一个物体或一个整体平均分成几份,每份就是这个物体或整体的几分之一。
几分之几:把一个物体或图形平均分成若干份,取这样的几份就是几分之几。
3.分数的读法:读分数从下往上读,先读分母,再读分数线(读作“分之”),再读分子。
4.分数的写法:写分数时,先写分数线,表示先平均分;再写分母表示平均分的份数;最后写分子,表示取几份。
5.比大小:同分母分数相比较,分子越大,分数就越大。
同分母分数相比较,分子越大,分数就越大。
分数的简单计算
1.同分母分数的加减法的原理:同分母分数相加减,分母不变,分子相加或相减。
2.1减几分之几的计算方法:1减几分之几,把1写成与减数分母相同的分数来计算。
同分母分数相加减,分母不变,分子相加或相减。
解决问题
1.我们既可以把一个完整的图形可以看作整体“1”,也可以把由多个个体组合在一起的图形或者物体看作整体“1”,用分数表示由多个个体组成的整体中的1份或几份时,整体份数就是这个分数的分母,其中,要表示的一份或几份就是这个分数的分子。
2.求一个数的几分之几是多少,就是用这个数除以分母,求出一份是多少,再用商乘分子。
求一个数的几分之几是多少,就是用这个数除以分母,求出一份是多少,再用商乘分子。
教材提示
目标导向
1.会用分数表示阴影部分的面积。
2.理解简单的有关分数的应用题,初步了解分数的乘除法计算。
重点导学
用分数表示阴影部分的面积。
难点剖析
了解分数的乘除法计算。
教材新解
教材讲解
知识点1 用分数表示阴影的面积。
【例】(1)用分数表示涂色部分。
【分析】1.理解题意。
中第一幅图是把一个正方形平均分成4份,其中的一份涂上了颜色,要求以那个分数表示涂色部分;第二幅图是把一个正方形剪成了4个相同的小正方形,其中的一个小正方形涂上了颜色,要求用分数表示涂色部分。
中把留个苹果看成一个整体,平均分成3份,每份2个。
2.用分数表示涂色部分。
中第一个分数是。把一个正方形平均分成4份,是把这个正方形看作整体“1”,涂色部分是其中的1份,是它的,所以用表示。
第二个分数也是,把一个正方形剪成了4个相同的小正方形,我们把小正方形的总数看作整体“1”,即把整体“1”平均分成4份,涂色部分占了一份,是它的,所以用表示。
(2)6个苹果平均分成3份,这里把苹果总数圈起来,看作一个整体“1”,即把整体“1”平均分成3份,分母是3,1份是苹果总数的,2份是苹果总数的,3份是苹果总数的。
【解答】
(1)
【知识归纳】
我们既可以把一个完整的图形可以看作整体“1”,也可以把由多个个体组合在一起的图形或者物体看作整体“1”,用分数表示由多个个体组成的整体中的1份或几份时,整体份数就是这个分数的分母,其中,要表示的一份或几份就是这个分数的分子。
知识点2 求一个数的几分之几是多少
【例】有12名学生,其中是女生,是男生。男女生各有多少人?
【分析】1.理解题意。
12名学生是总数,是女生,是男生,是说明12名学生看成一个整体,把这个整体平均分成3份,女生占其中的一份,男生占2份。求男女生各有多少人,就是求着1份和2份各是多少。如下图所示:
女生是,就是把总人数12平均分成3份,求出1份的人数。用除法计算,12÷3=4(人)。
男生是,就是把总人数12平均分成3份,求出2份的人数。用除法计算,12÷3=4(人),4×2=8(人)。
我们还可以用总人数减去女生的人数就是男生的人数。12-4=8(人)。
【解答】
12÷3=4(人)
4×2=8(人)
答:女生有4人,男生有8人。
【知识归纳】
求一个数的几分之几是多少,就是用这个数除以分母,求出一份是多少,再用商乘分子。
误区点拨
【误区1】用分数表示下图中的阴影部分
错误解答:
误区分析:此题错在没有平均分。
正确解答:
提示:如果在图中画几条虚线,如图,便可看出阴影部分占这个长方形的,将图二右上角的阴影部分移至左下角,与左下角圆的合在一起变成整个正方形的。
【误区2】判断:数学兴趣小组有7名男生、3名女生,女生人数占数学兴趣小组的。( )
错误解答:√
误区分析:此题错把男生人数当做了整体,题中数学兴趣小组总人数是7+3=10(人)。女生应该占。
正确解答:×
提示:用分数表示时,不要混淆了整体和部分。
典型剖析
【例1】如下图涂红色的部分占整个图形的( );涂蓝色的部分占整个图形的( ); 涂蓝色的部分比涂红色部分多占( )。
【思路点拨】整个图形被平均分成了9份,每份就是,涂红色部分占了其中的4 份,是4个,涂蓝色部分占了其中的5分,是5个,用蓝色部分减红色部分时,根据同分母分数相加减,分母不变,分子相加减。
【解答】红色部分占整个图形的,蓝色部分占整个图形的,蓝色部分比红色部分多占 -= 。
【知识归纳】
用分数表示由多个个体组成的整体中的1份或几份时,整体份数就是这个分数的分母,其中,要表示的一份或几份就是这个分数的分子。
【例2】图中阴影部分占整个图形的几分之几?
【思路点拨】用割补法改变阴影部分的形状。
如图: 因此,阴影部分占整个图形的。
【解答】
【知识归纳】
用分数表示阴影部分的面积时,我们可以先采用割补法改变阴影部分的形状,然后再表示。
【例3】30个苹果的、各是多少?
【思路点拨】把30个苹果看成一个整体,求它的,也就是求把30个苹果平均分成6份,其中的5份是多少,列式为30÷6×5=25(个)。求它的,也就是求把30个苹果平均分成5份,其中的3份是多少,列式为30÷5×3=18(个)。
【解答】30÷6×5=25(个)
30÷5×3=18(个)
答:30个苹果的是25个,是18个。
【知识归纳】
分数的分子不是1时,表示的份数不是其中一份的数量,分子是几,表示的就是其中几份的数量。
分数小故事
一天,妈妈在市场上买回5块大小不同的饼,要平均分给爸爸、妈妈、姥爷、姥姥和我。妈妈问我:“怎么才能平均每人分到的份数一样多?”这下可难住我了。
就在这个时候,我突然想起来,原来杨老师教我们的:如果有6个人,每人分到几个的问题,于是,我对妈妈说:“一共有5个人,先把最大的饼平均分成五分之一,再把第二大的饼平均分成五分之一,然后把第三大的饼平均分成五分之一,接着把第四大的饼平均分成五分之一,最后把最小的饼平均分成五分之一,这样每个人从这五个饼中分别都取五分之一,加到一块,得到的饼一就样多了”。妈妈夸我真聪明,吃饼的时候还多给我一块呢。
今天我真高兴!
第八单元小结
具体内容
重点知识
分数的初步认识
几分之一:把一个物体或一个整体平均分成几份,每份就是这个物体或整体的几分之一。
几分之几:把一个物体或图形平均分成若干份,取这样的几份就是几分之几。
3.分数的读法:读分数从下往上读,先读分母,再读分数线(读作“分之”),再读分子。
4.分数的写法:写分数时,先写分数线,表示先平均分;再写分母表示平均分的份数;最后写分子,表示取几份。
5.比大小:同分母分数相比较,分子越大,分数就越大。
同分母分数相比较,分子越大,分数就越大。
分数的简单计算
1.同分母分数的加减法的原理:同分母分数相加减,分母不变,分子相加或相减。
2.1减几分之几的计算方法:1减几分之几,把1写成与减数分母相同的分数来计算。
同分母分数相加减,分母不变,分子相加或相减。
解决问题
1.我们既可以把一个完整的图形可以看作整体“1”,也可以把由多个个体组合在一起的图形或者物体看作整体“1”,用分数表示由多个个体组成的整体中的1份或几份时,整体份数就是这个分数的分母,其中,要表示的一份或几份就是这个分数的分子。
2.求一个数的几分之几是多少,就是用这个数除以分母,求出一份是多少,再用商乘分子。
求一个数的几分之几是多少,就是用这个数除以分母,求出一份是多少,再用商乘分子。
