人教版三年级上册数学《教材新解》 1 分数的初步认识 1.2 几分之几 同步教材详解(Word版有答案)
文档属性
| 名称 | 人教版三年级上册数学《教材新解》 1 分数的初步认识 1.2 几分之几 同步教材详解(Word版有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 00:00:00 | ||
图片预览

文档简介
1.2 几分之几(教材P92~95)
教材提示
目标导向
1.初步认识几分之几,会读、会写几分之几,知道分数各部分的名称。
2.理解一些简单分数的具体含义,会比较同分母分数的大小。
重点导学
会读、会写几分之几,知道分数各部分名称。
难点剖析
比较同分母分数的大小。分母相同的分数,分子大的分数值比较大。
教材新解
教材讲解
知识点1 认识几分之几
【例】把一张正方形纸折成同样大的4份,再把一份或几份涂上颜色。
注:作图时,图片不要字。
【分析】1.理解题意。
把一张正方形纸折成同样大的4份,再把一份或几份涂上颜色,要求用分数表示涂色部分。所写出的分数的分母都是4,取其中几份,分子就是几。
具体解说。
(1)把一张正方形平均分成4份,每份就是这张纸的。
(2)把一张正方形平均分成4份,2份就是这张纸的。
(3)把一张正方形平均分成4份,3份就是这张纸的。
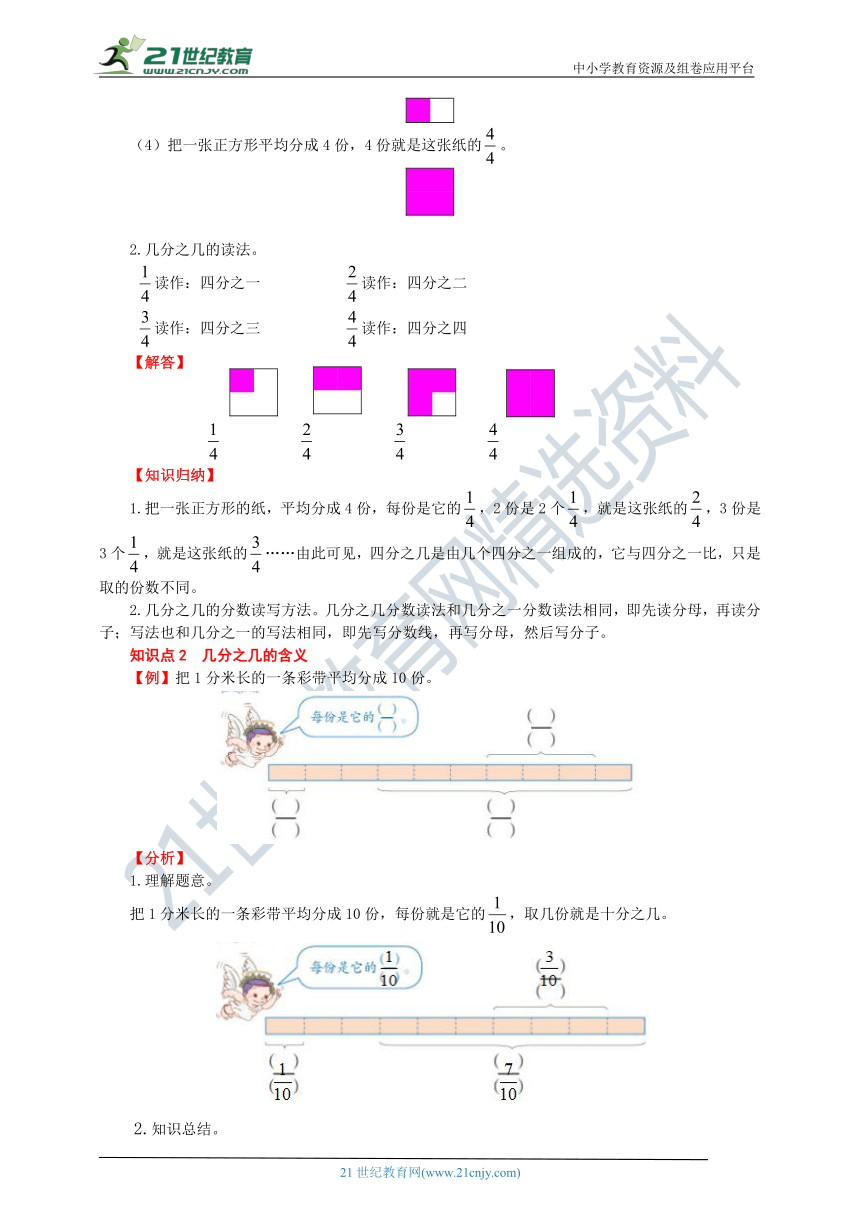
(4)把一张正方形平均分成4份,4份就是这张纸的。
几分之几的读法。
读作:四分之一 读作:四分之二
读作:四分之三 读作:四分之四
【解答】
【知识归纳】
1.把一张正方形的纸,平均分成4份,每份是它的,2份是2个,就是这张纸的,3份是3个,就是这张纸的……由此可见,四分之几是由几个四分之一组成的,它与四分之一比,只是取的份数不同。
2.几分之几的分数读写方法。几分之几分数读法和几分之一分数读法相同,即先读分母,再读分子;写法也和几分之一的写法相同,即先写分数线,再写分母,然后写分子。
知识点2 几分之几的含义
【例】把1分米长的一条彩带平均分成10份。
【分析】
理解题意。
把1分米长的一条彩带平均分成10份,每份就是它的,取几份就是十分之几。
2.知识总结。
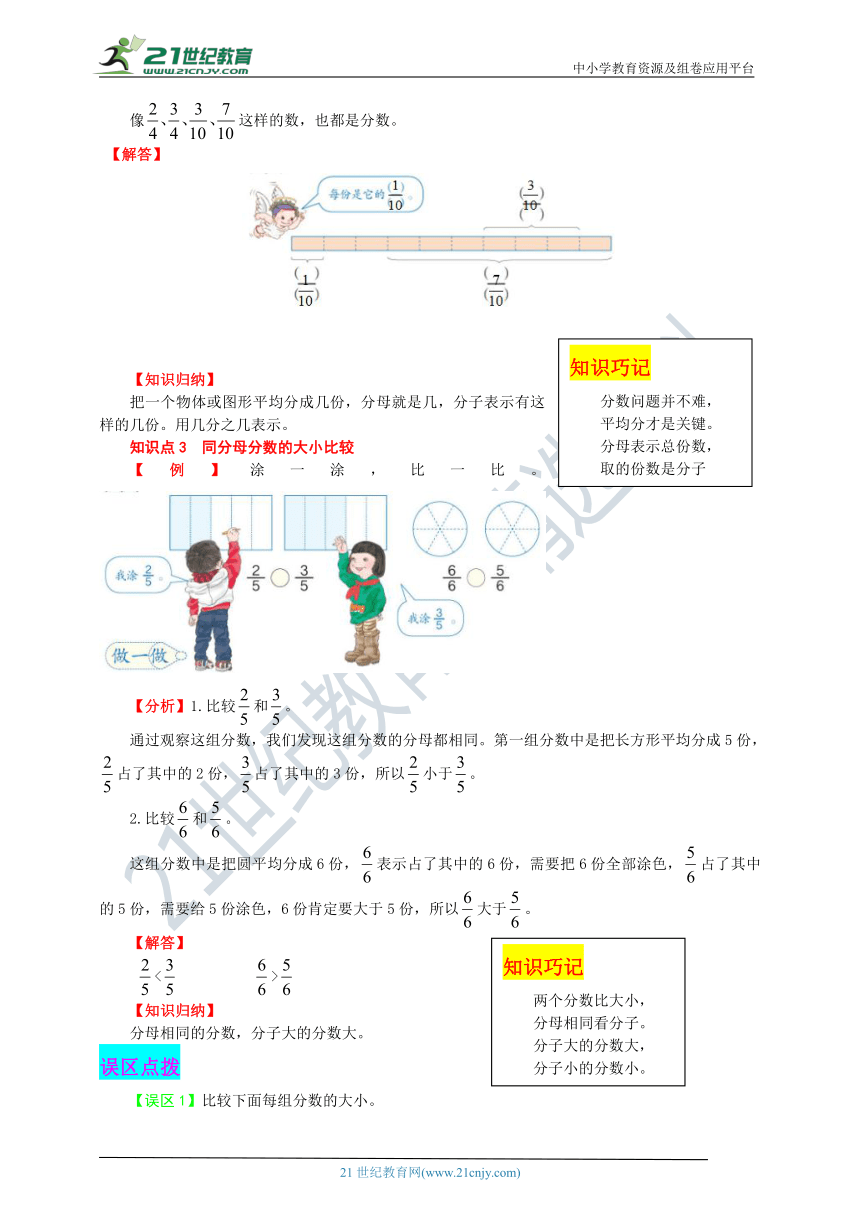
像这样的数,也都是分数。
【解答】
【知识归纳】
把一个物体或图形平均分成几份,分母就是几,分子表示有这样的几份。用几分之几表示。
知识点3 同分母分数的大小比较
【例】涂一涂,比一比。
【分析】1.比较和。
通过观察这组分数,我们发现这组分数的分母都相同。第一组分数中是把长方形平均分成5份,占了其中的2份,占了其中的3份,所以小于。
比较和。
这组分数中是把圆平均分成6份,表示占了其中的6份,需要把6份全部涂色,占了其中的5份,需要给5份涂色,6份肯定要大于5份,所以大于。
【解答】
< >
【知识归纳】
分母相同的分数,分子大的分数大。
误区点拨
【误区1】比较下面每组分数的大小。
错误解答:> >
误区分析:此题错在认为分子小的分数反而大。是1个,是3个,1个比3个小,所以<。是把正方形平均分成9份,取其中的1份,是把同样大的正方形平均分成9份,取其中的4份,1份是,4份是4个。
正确解答:< <
提示:分母相同的分数,分子大的分数值比较大。
典型剖析
【例1】用分数表示下图中的阴影部分。
(1) (2) (3)
【思路点拨】(1)中是把正方形平均分成4份,每份是它的,阴影部分占了3 份是3个,也就是。(2)中是把八边形平均分成8份,每份是它的,阴影部分占 了7份是7个,也就是。(3)中是把一个长方形平均分成10份,每份是它的, 阴影部分占9份是9个,也就是。
【解答】(1) (2) (3)
【知识归纳】
本题考查的是对几分之几分数的初步认识,会根据图形看出所表示的分数。
【例2】涂一涂,比一比。
○
【思路点拨】这组分数通过观察可发现其分母相同,都是6,那么可以根据“分母相同的分数,分子大的分数比较大”来比较,这个分数表把一个圆平均分成6份,占这样的6份,即全部,就是1,而表示这样的5份,即一部分。
【解答】
○
【知识归纳】
把一个物体或图形平均分成了几份,分母就是几,表示这样的几份,分子就是几。比较同分母的分数时,分子越大,分数就越大。
【例3】写出下面阴影部分表示的分数,再比较大小。
( ) ○ ( )
【思路点拨】这两幅图大小相同,但分的份数和取的份数都不相同,我们已经会比较分子是1的两个分数或分母相同的分数的大小,所以只有把上图转变成分母相同或分子是1的两个分数才能进行比较,把右图添加一些辅助线,使右图的分法和左图相同,就可以解答这个问题。
【解答】
=
【知识归纳】
有一些分数的分子分母不同,可以通过添加辅助线或去掉一些线的方法,帮助解决问题。
小马虎数鸡
春节里,养鸡专业户小马虎站在院子里,数了一遍鸡的总数,决定留下外,把慰问解放军,送给养老院。他把鸡送走后,听到房内有鸡叫,才知道少数了10只鸡。于是把房内房外的鸡重数一遍,没有错,不多不少,正是留下的数。小马虎奇怪了。问题出在哪里呢?你知道小马虎在院里数的鸡是多少只吗?
教材提示
目标导向
1.初步认识几分之几,会读、会写几分之几,知道分数各部分的名称。
2.理解一些简单分数的具体含义,会比较同分母分数的大小。
重点导学
会读、会写几分之几,知道分数各部分名称。
难点剖析
比较同分母分数的大小。分母相同的分数,分子大的分数值比较大。
教材新解
教材讲解
知识点1 认识几分之几
【例】把一张正方形纸折成同样大的4份,再把一份或几份涂上颜色。
注:作图时,图片不要字。
【分析】1.理解题意。
把一张正方形纸折成同样大的4份,再把一份或几份涂上颜色,要求用分数表示涂色部分。所写出的分数的分母都是4,取其中几份,分子就是几。
具体解说。
(1)把一张正方形平均分成4份,每份就是这张纸的。
(2)把一张正方形平均分成4份,2份就是这张纸的。
(3)把一张正方形平均分成4份,3份就是这张纸的。
(4)把一张正方形平均分成4份,4份就是这张纸的。
几分之几的读法。
读作:四分之一 读作:四分之二
读作:四分之三 读作:四分之四
【解答】
【知识归纳】
1.把一张正方形的纸,平均分成4份,每份是它的,2份是2个,就是这张纸的,3份是3个,就是这张纸的……由此可见,四分之几是由几个四分之一组成的,它与四分之一比,只是取的份数不同。
2.几分之几的分数读写方法。几分之几分数读法和几分之一分数读法相同,即先读分母,再读分子;写法也和几分之一的写法相同,即先写分数线,再写分母,然后写分子。
知识点2 几分之几的含义
【例】把1分米长的一条彩带平均分成10份。
【分析】
理解题意。
把1分米长的一条彩带平均分成10份,每份就是它的,取几份就是十分之几。
2.知识总结。
像这样的数,也都是分数。
【解答】
【知识归纳】
把一个物体或图形平均分成几份,分母就是几,分子表示有这样的几份。用几分之几表示。
知识点3 同分母分数的大小比较
【例】涂一涂,比一比。
【分析】1.比较和。
通过观察这组分数,我们发现这组分数的分母都相同。第一组分数中是把长方形平均分成5份,占了其中的2份,占了其中的3份,所以小于。
比较和。
这组分数中是把圆平均分成6份,表示占了其中的6份,需要把6份全部涂色,占了其中的5份,需要给5份涂色,6份肯定要大于5份,所以大于。
【解答】
< >
【知识归纳】
分母相同的分数,分子大的分数大。
误区点拨
【误区1】比较下面每组分数的大小。
错误解答:> >
误区分析:此题错在认为分子小的分数反而大。是1个,是3个,1个比3个小,所以<。是把正方形平均分成9份,取其中的1份,是把同样大的正方形平均分成9份,取其中的4份,1份是,4份是4个。
正确解答:< <
提示:分母相同的分数,分子大的分数值比较大。
典型剖析
【例1】用分数表示下图中的阴影部分。
(1) (2) (3)
【思路点拨】(1)中是把正方形平均分成4份,每份是它的,阴影部分占了3 份是3个,也就是。(2)中是把八边形平均分成8份,每份是它的,阴影部分占 了7份是7个,也就是。(3)中是把一个长方形平均分成10份,每份是它的, 阴影部分占9份是9个,也就是。
【解答】(1) (2) (3)
【知识归纳】
本题考查的是对几分之几分数的初步认识,会根据图形看出所表示的分数。
【例2】涂一涂,比一比。
○
【思路点拨】这组分数通过观察可发现其分母相同,都是6,那么可以根据“分母相同的分数,分子大的分数比较大”来比较,这个分数表把一个圆平均分成6份,占这样的6份,即全部,就是1,而表示这样的5份,即一部分。
【解答】
○
【知识归纳】
把一个物体或图形平均分成了几份,分母就是几,表示这样的几份,分子就是几。比较同分母的分数时,分子越大,分数就越大。
【例3】写出下面阴影部分表示的分数,再比较大小。
( ) ○ ( )
【思路点拨】这两幅图大小相同,但分的份数和取的份数都不相同,我们已经会比较分子是1的两个分数或分母相同的分数的大小,所以只有把上图转变成分母相同或分子是1的两个分数才能进行比较,把右图添加一些辅助线,使右图的分法和左图相同,就可以解答这个问题。
【解答】
=
【知识归纳】
有一些分数的分子分母不同,可以通过添加辅助线或去掉一些线的方法,帮助解决问题。
小马虎数鸡
春节里,养鸡专业户小马虎站在院子里,数了一遍鸡的总数,决定留下外,把慰问解放军,送给养老院。他把鸡送走后,听到房内有鸡叫,才知道少数了10只鸡。于是把房内房外的鸡重数一遍,没有错,不多不少,正是留下的数。小马虎奇怪了。问题出在哪里呢?你知道小马虎在院里数的鸡是多少只吗?
