人教版三年级上册数学《教材新解》 1 四边形 同步教材详解(Word版有答案)
文档属性
| 名称 | 人教版三年级上册数学《教材新解》 1 四边形 同步教材详解(Word版有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 20:35:54 | ||
图片预览


文档简介
第七单元 长方形和正方形
单元导航
1.认识四边形,知道四边形的特点。
2.认识长方形,了解正方形的特征。
3.能计算常见四边形的周长。
1 四边形(教材P3~15)
教材提示
目标导向
1.直观感知四边形,认识四边形的特征,在分一分的过程中进一步掌握长方形、正方形的特征,并体会分类的数学思想。
2.培养观察、比较和抽象概括能力。
重点导学
掌握四边形的特征。
难点剖析
根据四边形的特征,画要求的四边形。
教材新解
教材讲解
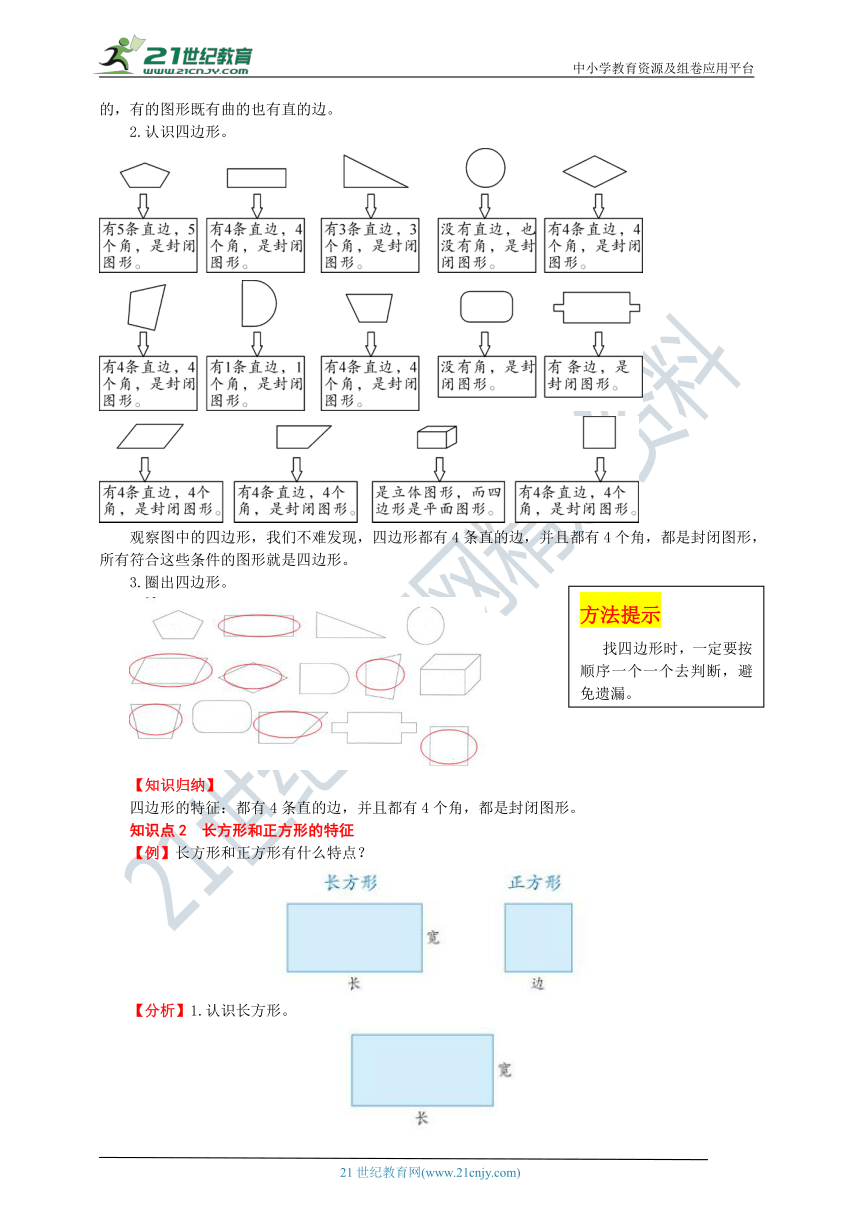
知识点1 四边形的特征
【例】把你认为是四边形的图形圈起来。
【分析】1.观察图形。
通过观察,我们发现,这些图形都是封闭的平面图形。有的图形的边是曲线,有的图形的边是直的,有的图形既有曲的也有直的边。
认识四边形。
观察图中的四边形,我们不难发现,四边形都有4条直的边,并且都有4个角,都是封闭图形,所有符合这些条件的图形就是四边形。
圈出四边形。
【知识归纳】
四边形的特征:都有4条直的边,并且都有4个角,都是封闭图形。
知识点2 长方形和正方形的特征
【例】长方形和正方形有什么特点?
【分析】1.认识长方形。
长方形对边相等,较长的边叫长方形的长,较短的边叫长方形的宽,4个角都是直角。
认识正方形。
正方形的4条边都相等,4个角都是直角。每条边叫正方形的边。
【知识归纳】
长方形对边相等,较长的边叫长方形的长,较短的边叫长方形的宽,4个角都是直角。
正方形的4条边都相等,4个角都是直角。每条边叫正方形的边。
误区点拨
【误区1】判断:和都是四边形。( )
错误解答:√
误区分析:此题错在没有掌握四边形的特点。左图虽然由四条线段组成,但没做到首尾连接;右图中有一条边是曲线,而不是线段。所以这两个图形都不是四边形。。
正确解答:×
提示:四边形是由四条线段围成的封闭图形。
【误区3】读出8009600。
错误解答:八百万零九千六百
误区分析:此题读错万级末尾的0。
正确解答:八百万九千六百
提示:此题考查学生对各个数级末尾含有0 的数的读法。8009600万级的数是800,按
【误区4】35008006的读法。
错误解答:三千五百万八千零零六
误区分析:此题读错个级中间的0。
正确解答:三千五百万八千零六
提示:此题考查学生对各个数级末尾含有0以及中间含有0的数的读法。万级的3500 【误区5】填空:三千五百万零七十写作:( )。
错误解答:3500070
误区分析:此题错在少写了一个0占位。
正确解答:35000070
提示:写较大的数时,不仅要从最高位写起,还要注意0的占位问题,当哪一位上一个
典型剖析
【例1】把图形分分类。
【思路点拨】
方法一:按给出图形角的特点进行分类:把四个角都是直角的图形分为一类,把四个角都不是直角的图形分为一类。
方法二:按照给出图形对边的特点进行分类:把两 组对边相等的图形分为一类;把有一组对边不相等的分为一类。
方法三:按照图形四条边的特点进行分类:把四条边都相等的图形分类一类;其他图形分为一类。
方法四:按照轴对称图形的特点分类:就是把轴对称图形的分为一类,不是轴对称图形的分为一类。
【知识归纳】
像这样按不同 标准将四边形分成不同的类别,体现的就是分类的数学思想。分类时要保证每次分类按照同一标准进行,并做到不重复、不遗漏,然后这些对象分类讨论。
【例2】看图填空。
1.从左往右数第( )个是圆形,第( )个是正方形,
2. 一共有( )个长方形。
【思路点拨】做这个题之前要了解各个图形的特点。
【解答】1.4 5 2.2
【知识归纳】
明确圆是一个曲线围成的图形,长方形和正方形都是特殊的四边形,长方形和正方形的四个角都是直角,长方形的对边相等,正方形的四条边都相等。
【例3】在下面的长方形 ABCD中任意画一条线段,把它分成两个完全相同的四边形。
【思路点拨】在长方形ABCD的长边AB、CD上分别取点E和点F,使AE=CF,连接E、F即是所要画的线段。因为长方形对边相等,所以AD=BC,当AE=CF时,EB=DF,EF为公共边,因此,四边形AEFD与四边形CFEB完全相同(如下图)。此外,还可以从宽边上画线段考虑。
【解答】
【知识归纳】
在长方形内画一条线段将该长方形分成大小、形状完全相同的四边形的方法:在长方形一组对边的不同方向取长度相同的一段描出两点,连接此两点即为所画的线段。
失踪的正方形
在一张正方形纸板上,按图一画上7×7=49个小正方形,然后沿图示直线剪切成5个小块。当你按照图二将这5小块纸板重新拼起的时候,你会发现不可思议的事情发生了:中间居然出现了一个洞!图一的正方形是由49个小正方形组成的。图二中却只有48个小正方形。哪一个小正方形没有了?它到哪儿去了?
图一 图二
原来5个小块图形中最大的两块2和3对换了一下位置以后,被那条对角线切开的每个小正方形都变得高比宽大了一点点。这就意味着这个大正方形已经不再是严格的正方形,它的高增加了,从而使得面积增加了,所增加的面积恰好等于这个方洞的面积。
单元导航
1.认识四边形,知道四边形的特点。
2.认识长方形,了解正方形的特征。
3.能计算常见四边形的周长。
1 四边形(教材P3~15)
教材提示
目标导向
1.直观感知四边形,认识四边形的特征,在分一分的过程中进一步掌握长方形、正方形的特征,并体会分类的数学思想。
2.培养观察、比较和抽象概括能力。
重点导学
掌握四边形的特征。
难点剖析
根据四边形的特征,画要求的四边形。
教材新解
教材讲解
知识点1 四边形的特征
【例】把你认为是四边形的图形圈起来。
【分析】1.观察图形。
通过观察,我们发现,这些图形都是封闭的平面图形。有的图形的边是曲线,有的图形的边是直的,有的图形既有曲的也有直的边。
认识四边形。
观察图中的四边形,我们不难发现,四边形都有4条直的边,并且都有4个角,都是封闭图形,所有符合这些条件的图形就是四边形。
圈出四边形。
【知识归纳】
四边形的特征:都有4条直的边,并且都有4个角,都是封闭图形。
知识点2 长方形和正方形的特征
【例】长方形和正方形有什么特点?
【分析】1.认识长方形。
长方形对边相等,较长的边叫长方形的长,较短的边叫长方形的宽,4个角都是直角。
认识正方形。
正方形的4条边都相等,4个角都是直角。每条边叫正方形的边。
【知识归纳】
长方形对边相等,较长的边叫长方形的长,较短的边叫长方形的宽,4个角都是直角。
正方形的4条边都相等,4个角都是直角。每条边叫正方形的边。
误区点拨
【误区1】判断:和都是四边形。( )
错误解答:√
误区分析:此题错在没有掌握四边形的特点。左图虽然由四条线段组成,但没做到首尾连接;右图中有一条边是曲线,而不是线段。所以这两个图形都不是四边形。。
正确解答:×
提示:四边形是由四条线段围成的封闭图形。
【误区3】读出8009600。
错误解答:八百万零九千六百
误区分析:此题读错万级末尾的0。
正确解答:八百万九千六百
提示:此题考查学生对各个数级末尾含有0 的数的读法。8009600万级的数是800,按
【误区4】35008006的读法。
错误解答:三千五百万八千零零六
误区分析:此题读错个级中间的0。
正确解答:三千五百万八千零六
提示:此题考查学生对各个数级末尾含有0以及中间含有0的数的读法。万级的3500 【误区5】填空:三千五百万零七十写作:( )。
错误解答:3500070
误区分析:此题错在少写了一个0占位。
正确解答:35000070
提示:写较大的数时,不仅要从最高位写起,还要注意0的占位问题,当哪一位上一个
典型剖析
【例1】把图形分分类。
【思路点拨】
方法一:按给出图形角的特点进行分类:把四个角都是直角的图形分为一类,把四个角都不是直角的图形分为一类。
方法二:按照给出图形对边的特点进行分类:把两 组对边相等的图形分为一类;把有一组对边不相等的分为一类。
方法三:按照图形四条边的特点进行分类:把四条边都相等的图形分类一类;其他图形分为一类。
方法四:按照轴对称图形的特点分类:就是把轴对称图形的分为一类,不是轴对称图形的分为一类。
【知识归纳】
像这样按不同 标准将四边形分成不同的类别,体现的就是分类的数学思想。分类时要保证每次分类按照同一标准进行,并做到不重复、不遗漏,然后这些对象分类讨论。
【例2】看图填空。
1.从左往右数第( )个是圆形,第( )个是正方形,
2. 一共有( )个长方形。
【思路点拨】做这个题之前要了解各个图形的特点。
【解答】1.4 5 2.2
【知识归纳】
明确圆是一个曲线围成的图形,长方形和正方形都是特殊的四边形,长方形和正方形的四个角都是直角,长方形的对边相等,正方形的四条边都相等。
【例3】在下面的长方形 ABCD中任意画一条线段,把它分成两个完全相同的四边形。
【思路点拨】在长方形ABCD的长边AB、CD上分别取点E和点F,使AE=CF,连接E、F即是所要画的线段。因为长方形对边相等,所以AD=BC,当AE=CF时,EB=DF,EF为公共边,因此,四边形AEFD与四边形CFEB完全相同(如下图)。此外,还可以从宽边上画线段考虑。
【解答】
【知识归纳】
在长方形内画一条线段将该长方形分成大小、形状完全相同的四边形的方法:在长方形一组对边的不同方向取长度相同的一段描出两点,连接此两点即为所画的线段。
失踪的正方形
在一张正方形纸板上,按图一画上7×7=49个小正方形,然后沿图示直线剪切成5个小块。当你按照图二将这5小块纸板重新拼起的时候,你会发现不可思议的事情发生了:中间居然出现了一个洞!图一的正方形是由49个小正方形组成的。图二中却只有48个小正方形。哪一个小正方形没有了?它到哪儿去了?
图一 图二
原来5个小块图形中最大的两块2和3对换了一下位置以后,被那条对角线切开的每个小正方形都变得高比宽大了一点点。这就意味着这个大正方形已经不再是严格的正方形,它的高增加了,从而使得面积增加了,所增加的面积恰好等于这个方洞的面积。
