人教版三年级上册数学《教材新解》第九单元 数学广角——集合 同步教材详解(Word版有答案)
文档属性
| 名称 | 人教版三年级上册数学《教材新解》第九单元 数学广角——集合 同步教材详解(Word版有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 00:00:00 | ||
图片预览

文档简介
第九单元 数学广角——集合
单元导航
会借助直观图,利用集合的思想方法解决简单的实际问题。
数学广角——集合(教材P104~107)
教材提示
目标导向
1.初步体会数的结合的思想方法将复杂问题简单化。
2.掌握集合思想在解决问题中的应用。
重点导学
运用集合思想解决实际问题。
难点剖析
正确理解集合图的含义。
教材新解
教材讲解
知识点1 利用集合的思想方法解决简单的实际问题
【例】下面是三(1)班参加跳绳、踢毽比赛的学生名单。
参加着两项比赛的共有多少人?
【分析】1.理解题意。
通过观察表格中的名单可以看出,参加跳绳比赛的有9人,参加踢毽比赛的有8人,要求参加这两项比赛的共有多少人,就用加法计算,列式为9+8=17(人)。但是从名单中看到参加这两项比赛的只有14人,而不是17人。这是因为有的同学参加了两项比赛,所以不能直接用两个数相加解决问题,应选择其他方法解决问题。
解题方法。
方法一:连线法。
把参加活动的学生名字分行列出,连线找到同时参加两项活动的人,就能找到9+8
中重复计算的学生了。
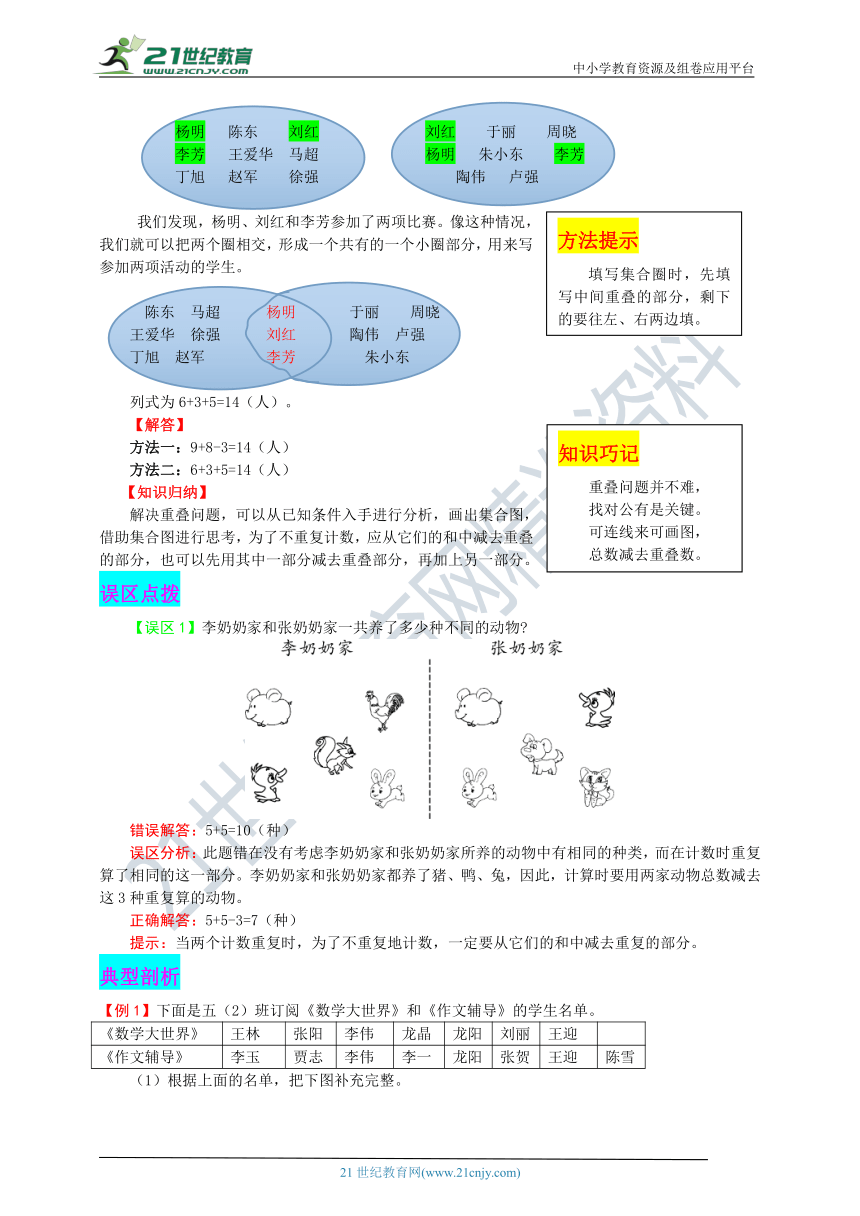
杨明 陈东 刘红 李芳 王爱华 马超 丁旭 赵军 徐强
刘红 于丽 周晓 杨明 朱小东 李芳 陶伟 卢强
我们发现,有3个人重复了,应该在总数里面减去3个人。即9+8-3=14(人)。
方法二:集合法。
把所有参加跳绳比赛的人放在一个圈里,再把所有参加踢毽比赛的人放在另一个圈里。
杨明 陈东 刘红 刘红 于丽 周晓
李芳 王爱华 马超 杨明 朱小东 李芳
丁旭 赵军 徐强 陶伟 卢强
我们发现,杨明、刘红和李芳参加了两项比赛。像这种情况,我们就可以把两个圈相交,形成一个共有的一个小圈部分,用来写参加两项活动的学生。
陈东 马超 杨明 于丽 周晓
王爱华 徐强 刘红 陶伟 卢强
丁旭 赵军 李芳 朱小东
列式为6+3+5=14(人)。
【解答】
方法一:9+8-3=14(人)
方法二:6+3+5=14(人)
【知识归纳】
解决重叠问题,可以从已知条件入手进行分析,画出集合图,借助集合图进行思考,为了不重复计数,应从它们的和中减去重叠的部分,也可以先用其中一部分减去重叠部分,再加上另一部分。
误区点拨
【误区1】李奶奶家和张奶奶家一共养了多少种不同的动物?
错误解答:5+5=10(种)
误区分析:此题错在没有考虑李奶奶家和张奶奶家所养的动物中有相同的种类,而在计数时重复算了相同的这一部分。李奶奶家和张奶奶家都养了猪、鸭、兔,因此,计算时要用两家动物总数减去这3种重复算的动物。
正确解答:5+5-3=7(种)
提示:当两个计数重复时,为了不重复地计数,一定要从它们的和中减去重复的部分。
典型剖析
【例1】下面是五(2)班订阅《数学大世界》和《作文辅导》的学生名单。
《数学大世界》
王林
张阳
李伟
龙晶
龙阳
刘丽
王迎
《作文辅导》
李玉
贾志
李伟
李一
龙阳
张贺
王迎
陈雪
(1)根据上面的名单,把下图补充完整。
(2)订阅《数学大世界》和《作文辅导》的共有多少人?
【思路点拨】(1)从订阅两种书的学生名单可以知道,订阅《数学大世界》的有7人,订阅《作文辅导》的有8人,两种书都订的有3人,把这3人填入两集合中重叠的那部分里。再把其他人分别填入两个集合圈中。
(2)计算订阅《数学大世界》和《作文辅导》的共有多少人时,先算出7+8=15(人),再减去被重复计算一次的3人,则15-3=12(人)。
【解答】(1)
(2)7+8-3=12(人) 答:订阅《数学大世界》和《作文辅导》的共有12人。
【知识归纳】
用集合的思想方法解决问题时,要想办法排除重复部分,做到不重复地计数。
【例2】三(2)班有42人,会打篮球的有21人,会游泳的有17人,两种运动都不会的有10人,两种运动都会的有多少人?
【思路点拨】从共有的42人中去掉两种运动都不会的10人,得到至少会一种 运动的人数42-10=32(人)。把会打篮球的和会游泳的人数合起来是21+17=38(人),这38人比至少会一种运动的同学数多38-32=6(人),多出的6人既在会打篮球的人数中算过,也在会游泳的人数中算过,是两种运动都会的人数。(如下图所示)
【解答】42-10=32(人) 21+17-32=6(人)
答:两种运动都会的有6人。
【知识归纳】
解答重叠问题,必须从条件入手进行分析,借助示意图进行思考,明确求的是哪一部分,从而找出解题方法。
重叠之美与数学
有重叠的地方往往就有美。中国民族风俗很讲究成双结对,文学里也有“双声”、“叠韵”等说法。在号称“人间天堂”的杭州,就有这样两副对联。其中之一是:
翠翠红红处处莺莺燕燕,
风风雨雨年年暮暮朝朝。
另一处则见于孤山中山公园的一座方亭,横匾题着“西湖天下景”五个大字,亭柱上悬挂一副楹联:
山山水水,处处明明秀秀;
晴晴雨雨,时时好好奇奇。
西湖的山山水水,处处明媚秀丽。这两幅对联写出了人们对杭州与西湖山水的共同感受,让人引起共鸣。不过对联的叠字毕竟有限,我们能否把重叠之美推向无限?这就得借助数学的力量了。出发点极其简单:3×4=12。
接下去可以写出第二式:33×34=1122。
重叠之美开始露头了,我们可以接下去看看第三式、第四式:333×334=111222;3333×3334=11112222。
当然重叠之美不限于此,只要你多留意,将来能够欣赏到更多的“数学之美”。“0”在《诗经》上的古义是“暴风雨末了的小雨滴”或是“暴风雨过后留在物体上的
第九单元小结
具体内容
重点知识
数学广角——集合
集合的思想方法:用集合的思想方法解决问题时,要想办法排除重复部分,做到不重复地计数。解决重叠问题时,可以从条件入手分析,画出示意图,借助示意图进行思考。
从条件入手分析,画出示意图,借助示意图进行思考。
单元导航
会借助直观图,利用集合的思想方法解决简单的实际问题。
数学广角——集合(教材P104~107)
教材提示
目标导向
1.初步体会数的结合的思想方法将复杂问题简单化。
2.掌握集合思想在解决问题中的应用。
重点导学
运用集合思想解决实际问题。
难点剖析
正确理解集合图的含义。
教材新解
教材讲解
知识点1 利用集合的思想方法解决简单的实际问题
【例】下面是三(1)班参加跳绳、踢毽比赛的学生名单。
参加着两项比赛的共有多少人?
【分析】1.理解题意。
通过观察表格中的名单可以看出,参加跳绳比赛的有9人,参加踢毽比赛的有8人,要求参加这两项比赛的共有多少人,就用加法计算,列式为9+8=17(人)。但是从名单中看到参加这两项比赛的只有14人,而不是17人。这是因为有的同学参加了两项比赛,所以不能直接用两个数相加解决问题,应选择其他方法解决问题。
解题方法。
方法一:连线法。
把参加活动的学生名字分行列出,连线找到同时参加两项活动的人,就能找到9+8
中重复计算的学生了。
杨明 陈东 刘红 李芳 王爱华 马超 丁旭 赵军 徐强
刘红 于丽 周晓 杨明 朱小东 李芳 陶伟 卢强
我们发现,有3个人重复了,应该在总数里面减去3个人。即9+8-3=14(人)。
方法二:集合法。
把所有参加跳绳比赛的人放在一个圈里,再把所有参加踢毽比赛的人放在另一个圈里。
杨明 陈东 刘红 刘红 于丽 周晓
李芳 王爱华 马超 杨明 朱小东 李芳
丁旭 赵军 徐强 陶伟 卢强
我们发现,杨明、刘红和李芳参加了两项比赛。像这种情况,我们就可以把两个圈相交,形成一个共有的一个小圈部分,用来写参加两项活动的学生。
陈东 马超 杨明 于丽 周晓
王爱华 徐强 刘红 陶伟 卢强
丁旭 赵军 李芳 朱小东
列式为6+3+5=14(人)。
【解答】
方法一:9+8-3=14(人)
方法二:6+3+5=14(人)
【知识归纳】
解决重叠问题,可以从已知条件入手进行分析,画出集合图,借助集合图进行思考,为了不重复计数,应从它们的和中减去重叠的部分,也可以先用其中一部分减去重叠部分,再加上另一部分。
误区点拨
【误区1】李奶奶家和张奶奶家一共养了多少种不同的动物?
错误解答:5+5=10(种)
误区分析:此题错在没有考虑李奶奶家和张奶奶家所养的动物中有相同的种类,而在计数时重复算了相同的这一部分。李奶奶家和张奶奶家都养了猪、鸭、兔,因此,计算时要用两家动物总数减去这3种重复算的动物。
正确解答:5+5-3=7(种)
提示:当两个计数重复时,为了不重复地计数,一定要从它们的和中减去重复的部分。
典型剖析
【例1】下面是五(2)班订阅《数学大世界》和《作文辅导》的学生名单。
《数学大世界》
王林
张阳
李伟
龙晶
龙阳
刘丽
王迎
《作文辅导》
李玉
贾志
李伟
李一
龙阳
张贺
王迎
陈雪
(1)根据上面的名单,把下图补充完整。
(2)订阅《数学大世界》和《作文辅导》的共有多少人?
【思路点拨】(1)从订阅两种书的学生名单可以知道,订阅《数学大世界》的有7人,订阅《作文辅导》的有8人,两种书都订的有3人,把这3人填入两集合中重叠的那部分里。再把其他人分别填入两个集合圈中。
(2)计算订阅《数学大世界》和《作文辅导》的共有多少人时,先算出7+8=15(人),再减去被重复计算一次的3人,则15-3=12(人)。
【解答】(1)
(2)7+8-3=12(人) 答:订阅《数学大世界》和《作文辅导》的共有12人。
【知识归纳】
用集合的思想方法解决问题时,要想办法排除重复部分,做到不重复地计数。
【例2】三(2)班有42人,会打篮球的有21人,会游泳的有17人,两种运动都不会的有10人,两种运动都会的有多少人?
【思路点拨】从共有的42人中去掉两种运动都不会的10人,得到至少会一种 运动的人数42-10=32(人)。把会打篮球的和会游泳的人数合起来是21+17=38(人),这38人比至少会一种运动的同学数多38-32=6(人),多出的6人既在会打篮球的人数中算过,也在会游泳的人数中算过,是两种运动都会的人数。(如下图所示)
【解答】42-10=32(人) 21+17-32=6(人)
答:两种运动都会的有6人。
【知识归纳】
解答重叠问题,必须从条件入手进行分析,借助示意图进行思考,明确求的是哪一部分,从而找出解题方法。
重叠之美与数学
有重叠的地方往往就有美。中国民族风俗很讲究成双结对,文学里也有“双声”、“叠韵”等说法。在号称“人间天堂”的杭州,就有这样两副对联。其中之一是:
翠翠红红处处莺莺燕燕,
风风雨雨年年暮暮朝朝。
另一处则见于孤山中山公园的一座方亭,横匾题着“西湖天下景”五个大字,亭柱上悬挂一副楹联:
山山水水,处处明明秀秀;
晴晴雨雨,时时好好奇奇。
西湖的山山水水,处处明媚秀丽。这两幅对联写出了人们对杭州与西湖山水的共同感受,让人引起共鸣。不过对联的叠字毕竟有限,我们能否把重叠之美推向无限?这就得借助数学的力量了。出发点极其简单:3×4=12。
接下去可以写出第二式:33×34=1122。
重叠之美开始露头了,我们可以接下去看看第三式、第四式:333×334=111222;3333×3334=11112222。
当然重叠之美不限于此,只要你多留意,将来能够欣赏到更多的“数学之美”。“0”在《诗经》上的古义是“暴风雨末了的小雨滴”或是“暴风雨过后留在物体上的
第九单元小结
具体内容
重点知识
数学广角——集合
集合的思想方法:用集合的思想方法解决问题时,要想办法排除重复部分,做到不重复地计数。解决重叠问题时,可以从条件入手分析,画出示意图,借助示意图进行思考。
从条件入手分析,画出示意图,借助示意图进行思考。
