人教版数学九年级下册28.1 锐角三角函数课件(第2课时 共30张PPT)
文档属性
| 名称 | 人教版数学九年级下册28.1 锐角三角函数课件(第2课时 共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 443.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-13 07:31:06 | ||
图片预览




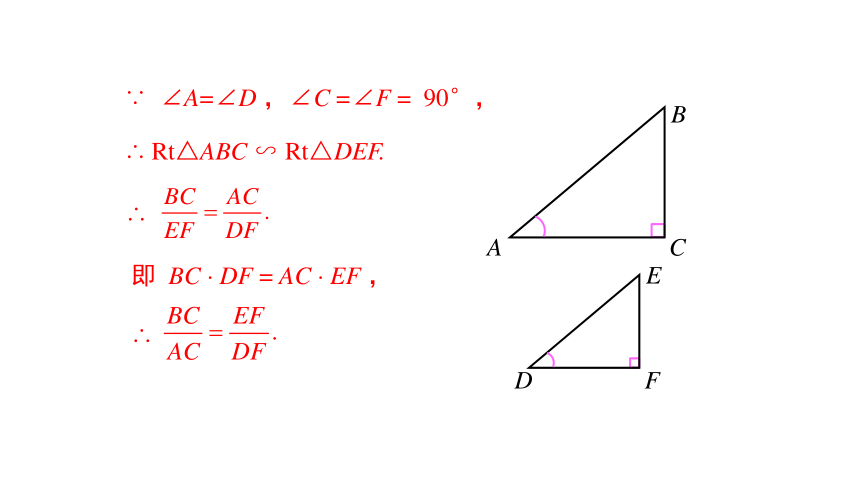
文档简介
课件30张PPT。
人教版 九年级数学下册
第28章 锐角三角函数
28.1 锐角三角函数(第2课时)
余弦函数和正切函数
1. 认识并理解余弦、正切的概念进而得到锐角三角函数的概念. (重点)
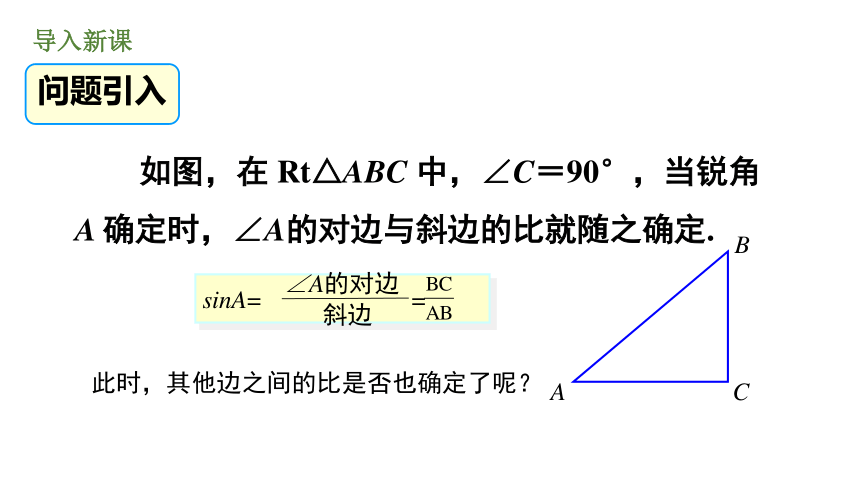
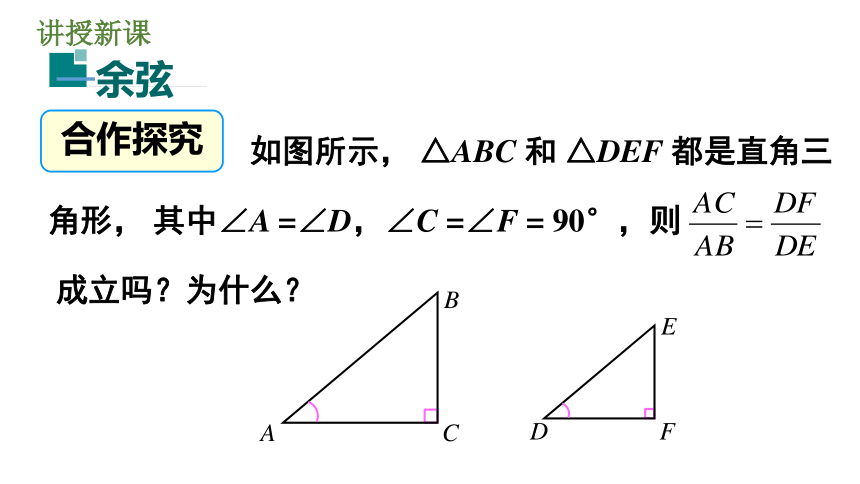
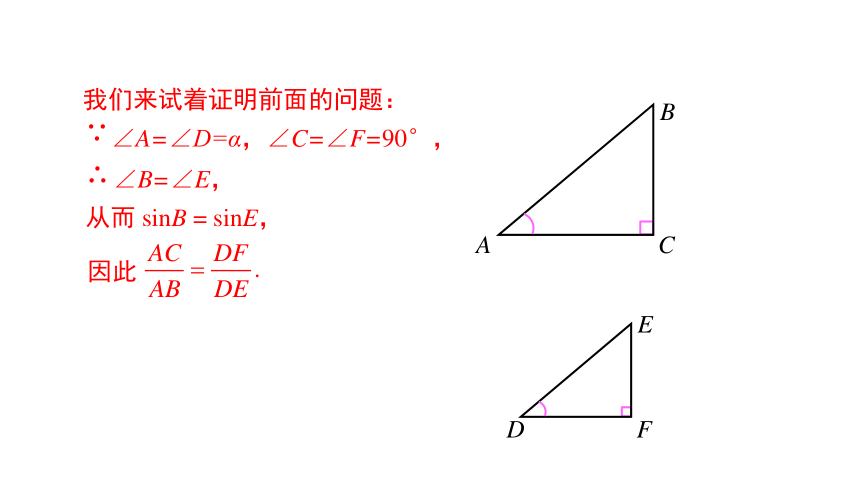
2. 能灵活运用锐角三角函数进行相关运算. (重点、难点)导入新课问题引入 如图,在 Rt△ABC 中,∠C=90°,当锐角 A 确定时,∠A的对边与斜边的比就随之确定. 此时,其他边之间的比是否也确定了呢?讲授新课合作探究我们来试着证明前面的问题:从而 sinB = sinE, 在有一个锐角相等的所有直角三角形中,这个锐角的邻边与斜边的比值是一个常数,与直角三角形的大小无关.
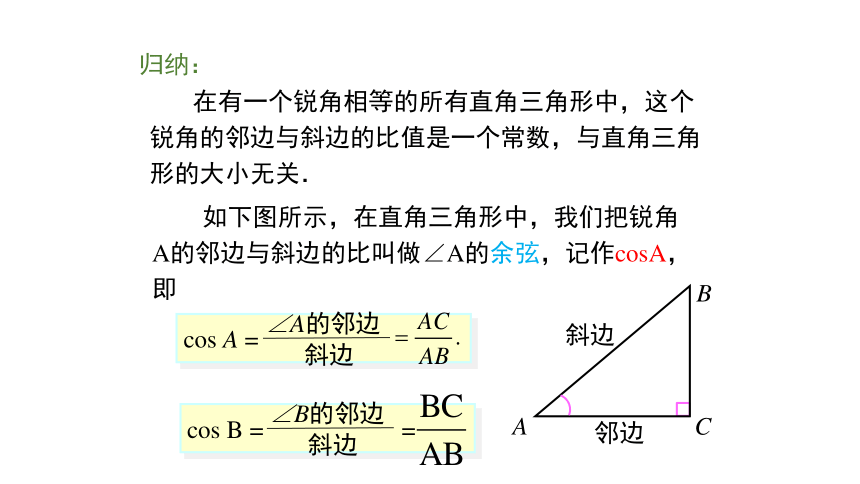
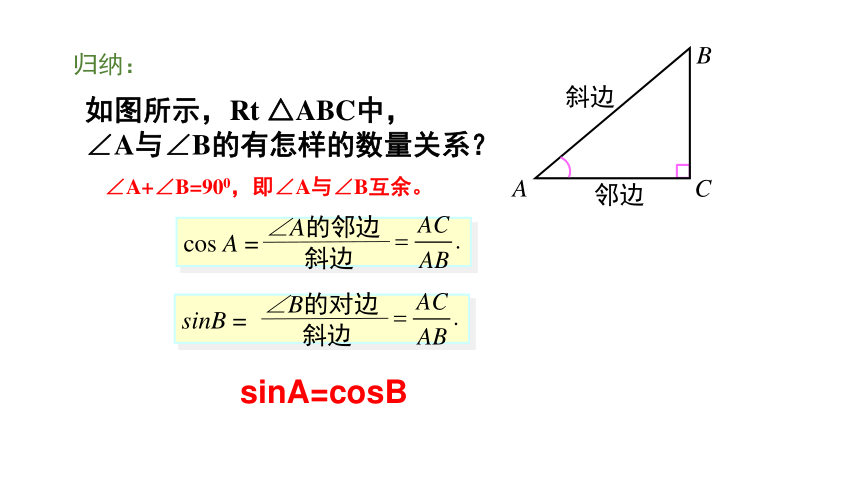
如下图所示,在直角三角形中,我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即归纳:斜边邻边归纳:斜边邻边如图所示,Rt △ABC中,
∠A与∠B的有怎样的数量关系?∠A+∠B=900,即∠A与∠B互余。sinA=cosB从上述探究和证明过程看出,对于任意锐角α,有
cos α = sin (90°-α)
从而有
sin α = cos (90°-α)
练一练1. 在 Rt△ABC 中,∠C=90°,AB=13,AC=12,
则cosA= .2. 已知sin30°= sin45°= sin60°=
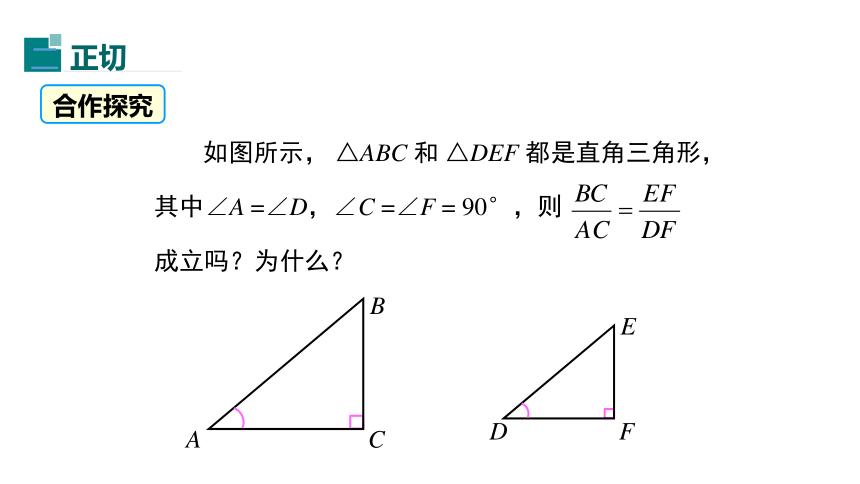
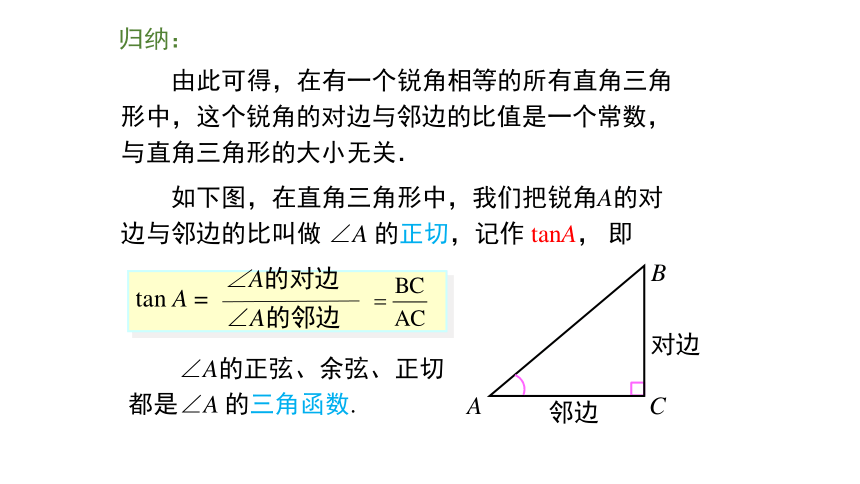
求 cos30°,cos45°,cos60°的值. 合作探究∴ Rt△ABC ∽ Rt△DEF.即 BC · DF = AC · EF , 由此可得,在有一个锐角相等的所有直角三角形中,这个锐角的对边与邻边的比值是一个常数,与直角三角形的大小无关. 如下图,在直角三角形中,我们把锐角A的对边与邻边的比叫做 ∠A 的正切,记作 tanA, 即归纳: ∠A的正弦、余弦、正切都是∠A 的三角函数. 如果两个角互余,那么这两个角的正切值有什么关系?想一想:如图所示,Rt △ABC中,∠A与∠B互余从上述探究和证明过程看出,对于任意锐角α,有
tanα? tan (90°-α)=1当∠A=45°时,tanA=?
当∠A<45°时,tanA
当∠A>45°时,tanA
tanA=1
tanA<1
tanA>1
1. 如图,平面直角坐标系中,若点 P 坐标为 (3,4),
则 tan ∠POQ=____.练一练2. 如图,△ABC 中一边 BC 与以 AC 为直径的 ⊙O
相切与点 C,若 BC=4,AB=5,则 tanA=___.例1 如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.解:由勾股定理得典例精析1. 在Rt△ABC中,∠C = 90°,AC = 12,AB =13.
sinA=______,cosA=______,tanA=____,
sinB=______,cosB=______,tanB=____.练一练2. 在Rt△ABC中,∠C=90°,AC=2,BC=3.
sinA=_______,cosA=_______,tanA=_____,
sinB=_______,cosB=_______,tanB=_____. 如图,在 Rt△ABC 中,∠C = 90°,AC = 8,
tanA= , 求sinA,cosB 的值.练一练1. 如图,在 Rt△ABC 中,斜边 AB 的长为 m,
∠A=35°,则直角边 BC 的长是 ( )A当堂练习2. 随着锐角 α 的增大,cosα 的值 ( )
A. 增大 B. 减小 C. 不变 D. 不确定B3. 已知 ∠A,∠B 为锐角,
(1) 若∠A =∠B,则 cosA cosB;
(2) 若 tanA = tanB,则∠A ∠B.
(3) 若 tanA · tanB = 1,则 ∠A 与 ∠B 的关系为:
.==4. tan30°= ,tan60°= . ∠A +∠B = 90°5. sin70°,cos70°,tan70°的大小关系是 ( )
A. tan70°<cos70°<sin70°
B. cos70°<tan70°<sin70°
C. sin70°<cos70°<tan70°
D. cos70°<sin70°<tan70°解析:根据锐角三角函数的概念,知 sin70°<1,cos70°<1,tan70°>1. 又∵cos70°=sin20°,正弦值随着角的增大而增大,∴sin70°>cos70°=sin20°. 故选D.D6. 如图,在 Rt△ABC 中,∠C = 90°,cosA = ,
求 sinA、tanA 的值.解:设 AC = 15k,则 AB = 17k.7. 如图,在 Rt△ABC 中,∠ACB = 90°,CD⊥AB,
垂足为 D. 若 AD = 6,CD = 8. 求 tanB 的值.解: ∵ ∠ACB= ∠ADC =90°,∴∠B+ ∠A=90°,
∠ACD+ ∠A =90°,∴∠B = ∠ACD,8. 如图,在△ABC中,AB=AC=4,BC=6. 求cosB 及
tanB 的值.解:过点 A 作 AD⊥BC 于 D.∵ AB = AC, ∴ BD = CD = 3,在 Rt△ABD 中D提示:求锐角的三角函数值的问题,当图形中没有直角三角形时,可以用恰当的方法构造直角三角形.课堂小结余弦函数和
正切函数在直角三角形中,锐角 A 的邻边与斜边的比叫做角 A 的余弦∠A的大小确定的情况下,cosA,tanA为定值,与三角形的大小无关在直角三角形中,锐角 A 的对边与邻边的比叫做角 A 的正切余弦正切性质作业布置:
必做题:1,2,3,4
选做题:512345
人教版 九年级数学下册
第28章 锐角三角函数
28.1 锐角三角函数(第2课时)
余弦函数和正切函数
1. 认识并理解余弦、正切的概念进而得到锐角三角函数的概念. (重点)
2. 能灵活运用锐角三角函数进行相关运算. (重点、难点)导入新课问题引入 如图,在 Rt△ABC 中,∠C=90°,当锐角 A 确定时,∠A的对边与斜边的比就随之确定. 此时,其他边之间的比是否也确定了呢?讲授新课合作探究我们来试着证明前面的问题:从而 sinB = sinE, 在有一个锐角相等的所有直角三角形中,这个锐角的邻边与斜边的比值是一个常数,与直角三角形的大小无关.
如下图所示,在直角三角形中,我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即归纳:斜边邻边归纳:斜边邻边如图所示,Rt △ABC中,
∠A与∠B的有怎样的数量关系?∠A+∠B=900,即∠A与∠B互余。sinA=cosB从上述探究和证明过程看出,对于任意锐角α,有
cos α = sin (90°-α)
从而有
sin α = cos (90°-α)
练一练1. 在 Rt△ABC 中,∠C=90°,AB=13,AC=12,
则cosA= .2. 已知sin30°= sin45°= sin60°=
求 cos30°,cos45°,cos60°的值. 合作探究∴ Rt△ABC ∽ Rt△DEF.即 BC · DF = AC · EF , 由此可得,在有一个锐角相等的所有直角三角形中,这个锐角的对边与邻边的比值是一个常数,与直角三角形的大小无关. 如下图,在直角三角形中,我们把锐角A的对边与邻边的比叫做 ∠A 的正切,记作 tanA, 即归纳: ∠A的正弦、余弦、正切都是∠A 的三角函数. 如果两个角互余,那么这两个角的正切值有什么关系?想一想:如图所示,Rt △ABC中,∠A与∠B互余从上述探究和证明过程看出,对于任意锐角α,有
tanα? tan (90°-α)=1当∠A=45°时,tanA=?
当∠A<45°时,tanA
当∠A>45°时,tanA
tanA=1
tanA<1
tanA>1
1. 如图,平面直角坐标系中,若点 P 坐标为 (3,4),
则 tan ∠POQ=____.练一练2. 如图,△ABC 中一边 BC 与以 AC 为直径的 ⊙O
相切与点 C,若 BC=4,AB=5,则 tanA=___.例1 如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.解:由勾股定理得典例精析1. 在Rt△ABC中,∠C = 90°,AC = 12,AB =13.
sinA=______,cosA=______,tanA=____,
sinB=______,cosB=______,tanB=____.练一练2. 在Rt△ABC中,∠C=90°,AC=2,BC=3.
sinA=_______,cosA=_______,tanA=_____,
sinB=_______,cosB=_______,tanB=_____. 如图,在 Rt△ABC 中,∠C = 90°,AC = 8,
tanA= , 求sinA,cosB 的值.练一练1. 如图,在 Rt△ABC 中,斜边 AB 的长为 m,
∠A=35°,则直角边 BC 的长是 ( )A当堂练习2. 随着锐角 α 的增大,cosα 的值 ( )
A. 增大 B. 减小 C. 不变 D. 不确定B3. 已知 ∠A,∠B 为锐角,
(1) 若∠A =∠B,则 cosA cosB;
(2) 若 tanA = tanB,则∠A ∠B.
(3) 若 tanA · tanB = 1,则 ∠A 与 ∠B 的关系为:
.==4. tan30°= ,tan60°= . ∠A +∠B = 90°5. sin70°,cos70°,tan70°的大小关系是 ( )
A. tan70°<cos70°<sin70°
B. cos70°<tan70°<sin70°
C. sin70°<cos70°<tan70°
D. cos70°<sin70°<tan70°解析:根据锐角三角函数的概念,知 sin70°<1,cos70°<1,tan70°>1. 又∵cos70°=sin20°,正弦值随着角的增大而增大,∴sin70°>cos70°=sin20°. 故选D.D6. 如图,在 Rt△ABC 中,∠C = 90°,cosA = ,
求 sinA、tanA 的值.解:设 AC = 15k,则 AB = 17k.7. 如图,在 Rt△ABC 中,∠ACB = 90°,CD⊥AB,
垂足为 D. 若 AD = 6,CD = 8. 求 tanB 的值.解: ∵ ∠ACB= ∠ADC =90°,∴∠B+ ∠A=90°,
∠ACD+ ∠A =90°,∴∠B = ∠ACD,8. 如图,在△ABC中,AB=AC=4,BC=6. 求cosB 及
tanB 的值.解:过点 A 作 AD⊥BC 于 D.∵ AB = AC, ∴ BD = CD = 3,在 Rt△ABD 中D提示:求锐角的三角函数值的问题,当图形中没有直角三角形时,可以用恰当的方法构造直角三角形.课堂小结余弦函数和
正切函数在直角三角形中,锐角 A 的邻边与斜边的比叫做角 A 的余弦∠A的大小确定的情况下,cosA,tanA为定值,与三角形的大小无关在直角三角形中,锐角 A 的对边与邻边的比叫做角 A 的正切余弦正切性质作业布置:
必做题:1,2,3,4
选做题:512345
