人教B版高中数学必修第一册 1.2.2全称量词命题与存在量词命题的否定学案
文档属性
| 名称 | 人教B版高中数学必修第一册 1.2.2全称量词命题与存在量词命题的否定学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 120.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-13 00:00:00 | ||
图片预览



文档简介
第一章 集合与常用逻辑用语
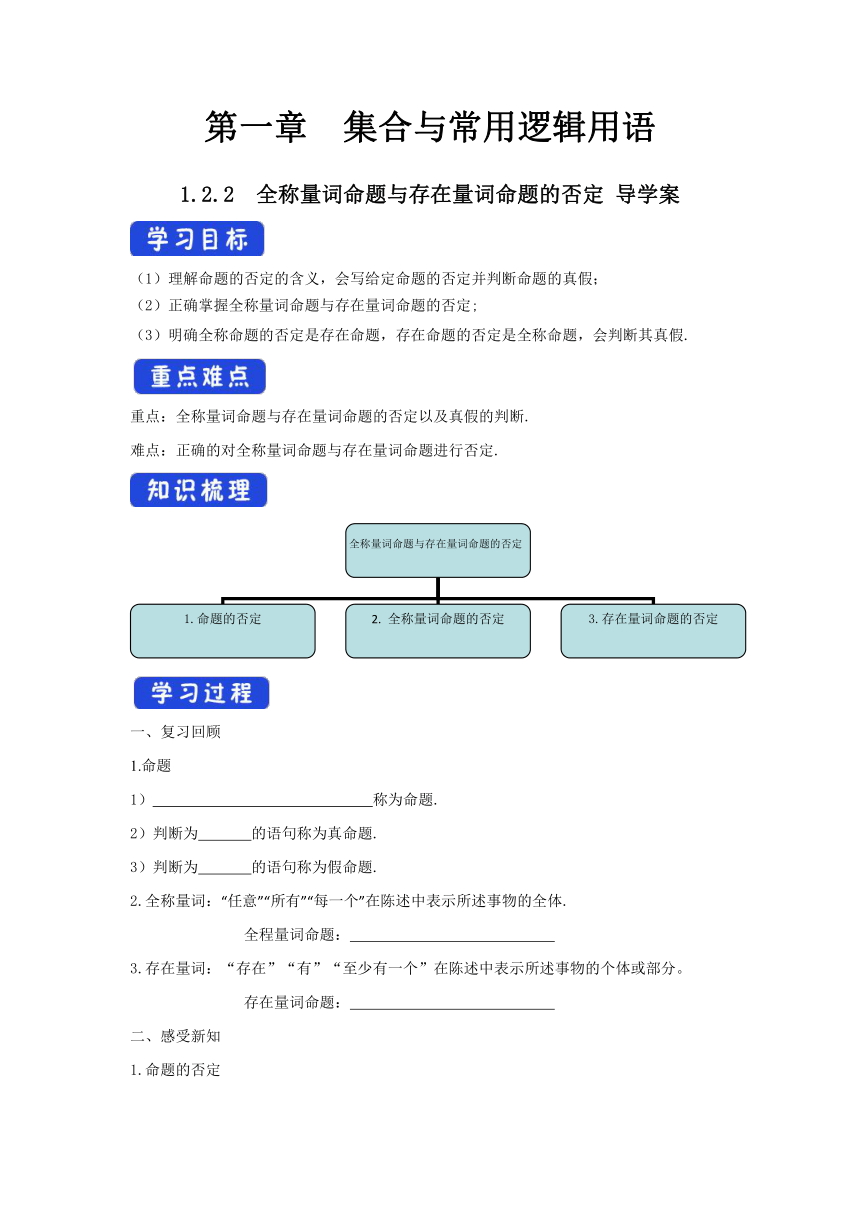
1.2.2 全称量词命题与存在量词命题的否定 导学案
(1)理解命题的否定的含义,会写给定命题的否定并判断命题的真假;
(2)正确掌握全称量词命题与存在量词命题的否定;
(3)明确全称命题的否定是存在命题,存在命题的否定是全称命题,会判断其真假.
重点:全称量词命题与存在量词命题的否定以及真假的判断.
难点:正确的对全称量词命题与存在量词命题进行否定.
一、复习回顾
1.命题
1) 称为命题.
2)判断为 的语句称为真命题.
3)判断为 的语句称为假命题.
2.全称量词:“任意”“所有”“每一个”在陈述中表示所述事物的全体.
全程量词命题:
3.存在量词:“存在”“有”“至少有一个”在陈述中表示所述事物的个体或部分。
存在量词命题:
二、感受新知
1.命题的否定
命题的否定: ,记作: ,读作:“非”或“的否定”。
(3)思考:命题与真假有什么关系呢?
命 题
命 题
归 纳 小 结
真
假
教材P29 练习A 1
2.全称量词命题与存在量词命题的否定
(1)下面我们来探究如何对全称量词命题与存在量词命题的否定进行否定.根据要求,认真思考回答问题:
1)命题
命 题
自然语言
存在整数是自然数。
符号语言
命题形式
真假判断
2)命题
命 题
自然语言
存在实数的平方小于0.
每一个实数的平方都不小于0。
符号语言
命题形式
真假判断
3)命题
命 题
自然语言
每一个有理数都是实数。
符号语言
命题形式
真假判断
(2)尝试与发现
记:“每一个素数都是奇数。”用类似的方法研究 和 的关系、符号表示以及真假性。
( )
命 题
自然语言
每一个素数都是奇数。
存在一个素数不是奇数。
符号语言
命题形式
真假判断
(3)想一想
全称量词命题的否定为:
存在量词命题的否定为:
3.经典例题
例1 写出下列命题的否定,并判断所得命题的真假:
(1)
(2)
(3) 至少有一个直角三角形不是等腰三角形。
例2 写出下列命题的否定,并判断所得命题的真假:
(1)
(2)
归纳方法:
教材P29 练习A 2、3 练习B 1
回顾本节课,你有什么收获?
作业:教材P29 练习B 2、3 教材P39 10
一、复习回顾
1.命题
1)可供真假判断的陈述语句称为命题.
2)判断为真的语句称为真命题.
3)判断为假的语句称为假命题.
2.全称量词:“任意”“所有”“每一个”在陈述中表示所述事物的全体.
全程量词命题:
3.存在量词:“存在”“有”“至少有一个”在陈述中表示所述事物的个体或部分。
存在量词命题:
二、感受新知
1.命题的否定
命题的否定:一般地,对命题加以否定,就得到一个新的命题,记作:“”,读作:“非”或“的否定”。
(3)思考:命题与真假有什么关系呢?
命 题
命 题
归 纳 小 结
命题与 的真假
相反
真
假
假
真
教材P29 练习A 1
解:(1) (2)
2.全称量词命题与存在量词命题的否定
(1)下面我们来探究如何对全称量词命题与存在量词命题的否定进行否定.根据要求,认真思考回答问题:
1)命题
命 题
自然语言
存在整数是自然数。
每一个整数都不是自然数。
符号语言
命题形式
存在量词命题
全称量词命题
真假判断
真命题
假命题
2)命题
命 题
自然语言
存在实数的平方小于0.
每一个实数的平方都不小于0。
符号语言
命题形式
存在量词命题
全称量词命题
真假判断
假命题
真命题
3)命题
命 题
自然语言
每一个有理数都是实数。
存在一个有理数不是实数。
符号语言
命题形式
全称量词命题
存在量词命题
真假判断
真命题
假命题
(2)尝试与发现
记:“每一个素数都是奇数。”用类似的方法研究 和 的关系、符号表示以及真假性。
( )
命 题
自然语言
每一个素数都是奇数。
存在一个素数不是奇数。
符号语言
命题形式
全称量词命题
存在量词命题
真假判断
假命题
真命题
(3)想一想:
全称量词命题的否定为:
存在量词命题的否定为:
3.经典例题
例1 写出下列命题的否定,并判断所得命题的真假:
解:(1)假命题
(2)真命题
(3) 所有直角三角形都是等腰三角形。假命题
例2 写出下列命题的否定,并判断所得命题的真假:
解:(1)假命题
(2) 真命题
归纳方法:
全称量词命题或存在量词命题的否定真假判断的策略。(1)写出该全称量词命题或存在量词命题的否定,在判断真假;(2)根据命题与其否定的真假相反可以转化为判断原全称量词命题或存在量词命题的真假。
1.2.2 全称量词命题与存在量词命题的否定 导学案
(1)理解命题的否定的含义,会写给定命题的否定并判断命题的真假;
(2)正确掌握全称量词命题与存在量词命题的否定;
(3)明确全称命题的否定是存在命题,存在命题的否定是全称命题,会判断其真假.
重点:全称量词命题与存在量词命题的否定以及真假的判断.
难点:正确的对全称量词命题与存在量词命题进行否定.
一、复习回顾
1.命题
1) 称为命题.
2)判断为 的语句称为真命题.
3)判断为 的语句称为假命题.
2.全称量词:“任意”“所有”“每一个”在陈述中表示所述事物的全体.
全程量词命题:
3.存在量词:“存在”“有”“至少有一个”在陈述中表示所述事物的个体或部分。
存在量词命题:
二、感受新知
1.命题的否定
命题的否定: ,记作: ,读作:“非”或“的否定”。
(3)思考:命题与真假有什么关系呢?
命 题
命 题
归 纳 小 结
真
假
教材P29 练习A 1
2.全称量词命题与存在量词命题的否定
(1)下面我们来探究如何对全称量词命题与存在量词命题的否定进行否定.根据要求,认真思考回答问题:
1)命题
命 题
自然语言
存在整数是自然数。
符号语言
命题形式
真假判断
2)命题
命 题
自然语言
存在实数的平方小于0.
每一个实数的平方都不小于0。
符号语言
命题形式
真假判断
3)命题
命 题
自然语言
每一个有理数都是实数。
符号语言
命题形式
真假判断
(2)尝试与发现
记:“每一个素数都是奇数。”用类似的方法研究 和 的关系、符号表示以及真假性。
( )
命 题
自然语言
每一个素数都是奇数。
存在一个素数不是奇数。
符号语言
命题形式
真假判断
(3)想一想
全称量词命题的否定为:
存在量词命题的否定为:
3.经典例题
例1 写出下列命题的否定,并判断所得命题的真假:
(1)
(2)
(3) 至少有一个直角三角形不是等腰三角形。
例2 写出下列命题的否定,并判断所得命题的真假:
(1)
(2)
归纳方法:
教材P29 练习A 2、3 练习B 1
回顾本节课,你有什么收获?
作业:教材P29 练习B 2、3 教材P39 10
一、复习回顾
1.命题
1)可供真假判断的陈述语句称为命题.
2)判断为真的语句称为真命题.
3)判断为假的语句称为假命题.
2.全称量词:“任意”“所有”“每一个”在陈述中表示所述事物的全体.
全程量词命题:
3.存在量词:“存在”“有”“至少有一个”在陈述中表示所述事物的个体或部分。
存在量词命题:
二、感受新知
1.命题的否定
命题的否定:一般地,对命题加以否定,就得到一个新的命题,记作:“”,读作:“非”或“的否定”。
(3)思考:命题与真假有什么关系呢?
命 题
命 题
归 纳 小 结
命题与 的真假
相反
真
假
假
真
教材P29 练习A 1
解:(1) (2)
2.全称量词命题与存在量词命题的否定
(1)下面我们来探究如何对全称量词命题与存在量词命题的否定进行否定.根据要求,认真思考回答问题:
1)命题
命 题
自然语言
存在整数是自然数。
每一个整数都不是自然数。
符号语言
命题形式
存在量词命题
全称量词命题
真假判断
真命题
假命题
2)命题
命 题
自然语言
存在实数的平方小于0.
每一个实数的平方都不小于0。
符号语言
命题形式
存在量词命题
全称量词命题
真假判断
假命题
真命题
3)命题
命 题
自然语言
每一个有理数都是实数。
存在一个有理数不是实数。
符号语言
命题形式
全称量词命题
存在量词命题
真假判断
真命题
假命题
(2)尝试与发现
记:“每一个素数都是奇数。”用类似的方法研究 和 的关系、符号表示以及真假性。
( )
命 题
自然语言
每一个素数都是奇数。
存在一个素数不是奇数。
符号语言
命题形式
全称量词命题
存在量词命题
真假判断
假命题
真命题
(3)想一想:
全称量词命题的否定为:
存在量词命题的否定为:
3.经典例题
例1 写出下列命题的否定,并判断所得命题的真假:
解:(1)假命题
(2)真命题
(3) 所有直角三角形都是等腰三角形。假命题
例2 写出下列命题的否定,并判断所得命题的真假:
解:(1)假命题
(2) 真命题
归纳方法:
全称量词命题或存在量词命题的否定真假判断的策略。(1)写出该全称量词命题或存在量词命题的否定,在判断真假;(2)根据命题与其否定的真假相反可以转化为判断原全称量词命题或存在量词命题的真假。
