沪科版九下:24.4直线与圆的位置关系1 教案
文档属性
| 名称 | 沪科版九下:24.4直线与圆的位置关系1 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 32.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 00:00:00 | ||
图片预览



文档简介
《直线与圆的位置关系1》教案
课 题
直线和圆的位置关系1
课 型
新授课
第一课时
教学目标
知识与技能
使学生掌握直线和圆的三种位置关系的定义及其判定方法和性质
过程与方法
使学生从运动的观点来观察直线和圆相交、相切、相离的关系、培养学生的辩证唯
物主义观点.
情感态度与价值观
1.积极参与数学活动,对数学产生好奇心和求知欲.
2.形成实事求是的态度以及独立思考的习惯.
通过直线和圆的位置关系的探究,向学生渗透类比、分
类、数形结合的思想,培养学生观察、分析和发现问题
的能力;
教学重点
掌握直线和圆的三种位置关系的性质与判定
教学难点
如何引导学生发现隐含在图形中的两个数量d和r并加以比较.
教与学策略
指导-自主学习 引导—探索法
课前准备(教具、活动准备等)
在教学中应多利用投影演示加强直观,渗透思想,指导方法,加强引导,使他们不断由“学会”向“会学”发展。
教 学 过 程
教学步骤
教 师 活 动
学 生 活 动
设 计 意 图
创
设
问
题
情
境
,
引
入
新
课
学
生
自
学
,
探
究
新
知
学
生
自
学
,
探
究
新
知
合
作
交
流
,
再
探
新
知
例
题
讲
解
合
作
交
流
,
再
探
新
知
合
作
交
流
随
堂
练
习
知
识
回
顾
,
总
结
收
获
我们已经研究了点和圆的位置关系,回忆一下有几种情况?是怎样判定各个位置关系的?点和圆的位置关系是用什么方法研究?(演示投影或放录像)
今天我们将研究在同一平面内“直线和圆的位置关系”探索、学习新知识
①利用投影演示直线和圆的运动变化过程,引导学生观察,直线和圆的位置关系在哪些方面发生了变化?观察“公共点个数”的变化。
②引导学生思考:Ⅰ直线和圆有三个(或三个以上)的公共点吗?为什么?
Ⅱ通过刚才的研究,你认为直线和圆的位置关系可分为几种类型?分类的标准各是什么?
③在此基础上,揭示直线和圆的位置关系的定义(板书)
④提问:Ⅰ有人说:“直线和圆有一个公共点时,叫做直线和圆相切”,你说这句话对吗?为什么?
引导学生对照定义,揭示唯一的含义。
Ⅱ有人说:“当直线和圆相离时,直线和圆一定没有公共点”,你说对吗?为什么?
引导学生认识凡定义都可反过来作判定
2、直线和圆的位置关系的判定和性质
引导1:通过刚才的研究我们已经知道,借助公共点的个数可以判定,直线和圆的位置关系,那么请同学们思考一下,能否象判定点和圆的位置关系那样,用数量关系来判定直线和圆的位置关系呢?
引导2:点和圆的位置关系的判定运用了哪两个数量之间的关系?直线和圆的位置关系中可以出现哪些量呢?说出你的思考过程?
引导3:如何用图形来反映半径和圆心到直线的距离,这两个量呢?(投影)
引导4:如何由数量关系并结合观察图形判定相应的位置关系呢?从而板书判定(略)
能否根据点和圆的位置关系,点到圆心的距离d和半径r作比较,类似地推导出如何用点到直线的距离d和半径r之间的关系来确定三种位置关系呢
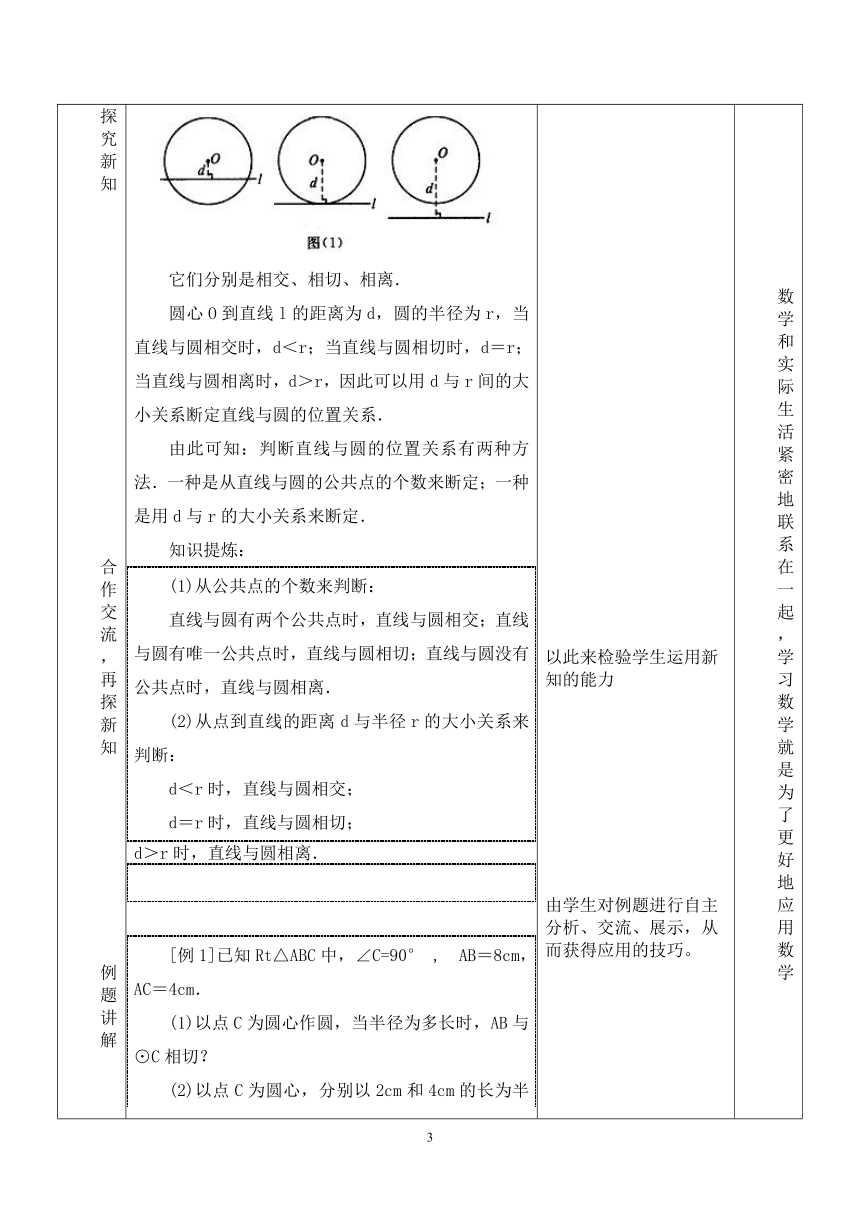
如图:
它们分别是相交、相切、相离.
圆心O到直线l的距离为d,圆的半径为r,当直线与圆相交时,d<r;当直线与圆相切时,d=r;当直线与圆相离时,d>r,因此可以用d与r间的大小关系断定直线与圆的位置关系.
由此可知:判断直线与圆的位置关系有两种方法.一种是从直线与圆的公共点的个数来断定;一种是用d与r的大小关系来断定.
知识提炼:
(1)从公共点的个数来判断:
直线与圆有两个公共点时,直线与圆相交;直线与圆有唯一公共点时,直线与圆相切;直线与圆没有公共点时,直线与圆相离.
(2)从点到直线的距离d与半径r的大小关系来判断:
d<r时,直线与圆相交;
d=r时,直线与圆相切;
d>r时,直线与圆相离.
[例1]已知Rt△ABC中,∠C=90° , AB=8cm,AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(2)以点C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
分析:根据d与r间的数量关系可知:
d=r时,相切;d<r时,相交;d>r时,相离.
解:(1)如上图,过点C作AB的垂线段CD.
∵AC=4cm,AB=8cm;
∴cosA=,
∴∠A=60°.
∴CD=ACsinA=4sin60°=2(cm).
因此,当半径长为2cm时,AB与⊙C相切.
(2)由(1)可知,圆心C到AB的距离d=2cm,所以,当r=2cm时,d>r,⊙C与AB相离;
当r=4cm时,d<r,⊙C与AB相交.
课堂练习
随堂练习
课堂小结
本节课学习了如下内容:
1.直线与圆的三种位置关系.
(1)从公共点数来判断.
(2)从d与r间的数量关系来判断.
2. 利用本节知识解决实际问题
直线和圆的位置关系(一)
1.复习点到直线的距离的定义
2.探索直线与圆的三种位置关系
(1)从公共点个数来判断
(2)从点到直线的距离d与半径r间的数量关系来判断
布置作业
目标检测
学生思考后口答
学生总结
学生归纳
以此来检验学生运用新知的能力
由学生对例题进行自主分析、交流、展示,从而获得应用的技巧。
学生谈收获与困惑
设
疑
激
趣
学生已经具备了自学的能力,能够按照要求完成任务。
设置问题串,由易到难符合学生的认知规律。
数
学
和
实
际
生
活
紧
密
地
联
系
在
一
起
,
学
习
数
学
就
是
为
了
更
好
地
应
用
数
学
合
作
交
流
培
养
学
生
的
合
作
意
识
渗透思想
题目设计基础性强,主要检测本节的基础内容。
课 题
直线和圆的位置关系1
课 型
新授课
第一课时
教学目标
知识与技能
使学生掌握直线和圆的三种位置关系的定义及其判定方法和性质
过程与方法
使学生从运动的观点来观察直线和圆相交、相切、相离的关系、培养学生的辩证唯
物主义观点.
情感态度与价值观
1.积极参与数学活动,对数学产生好奇心和求知欲.
2.形成实事求是的态度以及独立思考的习惯.
通过直线和圆的位置关系的探究,向学生渗透类比、分
类、数形结合的思想,培养学生观察、分析和发现问题
的能力;
教学重点
掌握直线和圆的三种位置关系的性质与判定
教学难点
如何引导学生发现隐含在图形中的两个数量d和r并加以比较.
教与学策略
指导-自主学习 引导—探索法
课前准备(教具、活动准备等)
在教学中应多利用投影演示加强直观,渗透思想,指导方法,加强引导,使他们不断由“学会”向“会学”发展。
教 学 过 程
教学步骤
教 师 活 动
学 生 活 动
设 计 意 图
创
设
问
题
情
境
,
引
入
新
课
学
生
自
学
,
探
究
新
知
学
生
自
学
,
探
究
新
知
合
作
交
流
,
再
探
新
知
例
题
讲
解
合
作
交
流
,
再
探
新
知
合
作
交
流
随
堂
练
习
知
识
回
顾
,
总
结
收
获
我们已经研究了点和圆的位置关系,回忆一下有几种情况?是怎样判定各个位置关系的?点和圆的位置关系是用什么方法研究?(演示投影或放录像)
今天我们将研究在同一平面内“直线和圆的位置关系”探索、学习新知识
①利用投影演示直线和圆的运动变化过程,引导学生观察,直线和圆的位置关系在哪些方面发生了变化?观察“公共点个数”的变化。
②引导学生思考:Ⅰ直线和圆有三个(或三个以上)的公共点吗?为什么?
Ⅱ通过刚才的研究,你认为直线和圆的位置关系可分为几种类型?分类的标准各是什么?
③在此基础上,揭示直线和圆的位置关系的定义(板书)
④提问:Ⅰ有人说:“直线和圆有一个公共点时,叫做直线和圆相切”,你说这句话对吗?为什么?
引导学生对照定义,揭示唯一的含义。
Ⅱ有人说:“当直线和圆相离时,直线和圆一定没有公共点”,你说对吗?为什么?
引导学生认识凡定义都可反过来作判定
2、直线和圆的位置关系的判定和性质
引导1:通过刚才的研究我们已经知道,借助公共点的个数可以判定,直线和圆的位置关系,那么请同学们思考一下,能否象判定点和圆的位置关系那样,用数量关系来判定直线和圆的位置关系呢?
引导2:点和圆的位置关系的判定运用了哪两个数量之间的关系?直线和圆的位置关系中可以出现哪些量呢?说出你的思考过程?
引导3:如何用图形来反映半径和圆心到直线的距离,这两个量呢?(投影)
引导4:如何由数量关系并结合观察图形判定相应的位置关系呢?从而板书判定(略)
能否根据点和圆的位置关系,点到圆心的距离d和半径r作比较,类似地推导出如何用点到直线的距离d和半径r之间的关系来确定三种位置关系呢
如图:
它们分别是相交、相切、相离.
圆心O到直线l的距离为d,圆的半径为r,当直线与圆相交时,d<r;当直线与圆相切时,d=r;当直线与圆相离时,d>r,因此可以用d与r间的大小关系断定直线与圆的位置关系.
由此可知:判断直线与圆的位置关系有两种方法.一种是从直线与圆的公共点的个数来断定;一种是用d与r的大小关系来断定.
知识提炼:
(1)从公共点的个数来判断:
直线与圆有两个公共点时,直线与圆相交;直线与圆有唯一公共点时,直线与圆相切;直线与圆没有公共点时,直线与圆相离.
(2)从点到直线的距离d与半径r的大小关系来判断:
d<r时,直线与圆相交;
d=r时,直线与圆相切;
d>r时,直线与圆相离.
[例1]已知Rt△ABC中,∠C=90° , AB=8cm,AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(2)以点C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
分析:根据d与r间的数量关系可知:
d=r时,相切;d<r时,相交;d>r时,相离.
解:(1)如上图,过点C作AB的垂线段CD.
∵AC=4cm,AB=8cm;
∴cosA=,
∴∠A=60°.
∴CD=ACsinA=4sin60°=2(cm).
因此,当半径长为2cm时,AB与⊙C相切.
(2)由(1)可知,圆心C到AB的距离d=2cm,所以,当r=2cm时,d>r,⊙C与AB相离;
当r=4cm时,d<r,⊙C与AB相交.
课堂练习
随堂练习
课堂小结
本节课学习了如下内容:
1.直线与圆的三种位置关系.
(1)从公共点数来判断.
(2)从d与r间的数量关系来判断.
2. 利用本节知识解决实际问题
直线和圆的位置关系(一)
1.复习点到直线的距离的定义
2.探索直线与圆的三种位置关系
(1)从公共点个数来判断
(2)从点到直线的距离d与半径r间的数量关系来判断
布置作业
目标检测
学生思考后口答
学生总结
学生归纳
以此来检验学生运用新知的能力
由学生对例题进行自主分析、交流、展示,从而获得应用的技巧。
学生谈收获与困惑
设
疑
激
趣
学生已经具备了自学的能力,能够按照要求完成任务。
设置问题串,由易到难符合学生的认知规律。
数
学
和
实
际
生
活
紧
密
地
联
系
在
一
起
,
学
习
数
学
就
是
为
了
更
好
地
应
用
数
学
合
作
交
流
培
养
学
生
的
合
作
意
识
渗透思想
题目设计基础性强,主要检测本节的基础内容。
