人教版数学八年级下册17.1 勾股定理 强化提升练习(含详细答案)
文档属性
| 名称 | 人教版数学八年级下册17.1 勾股定理 强化提升练习(含详细答案) |  | |
| 格式 | zip | ||
| 文件大小 | 300.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 19:41:32 | ||
图片预览


文档简介
17.1 勾股定理 强化提升练习
一.选择题(共10小题)
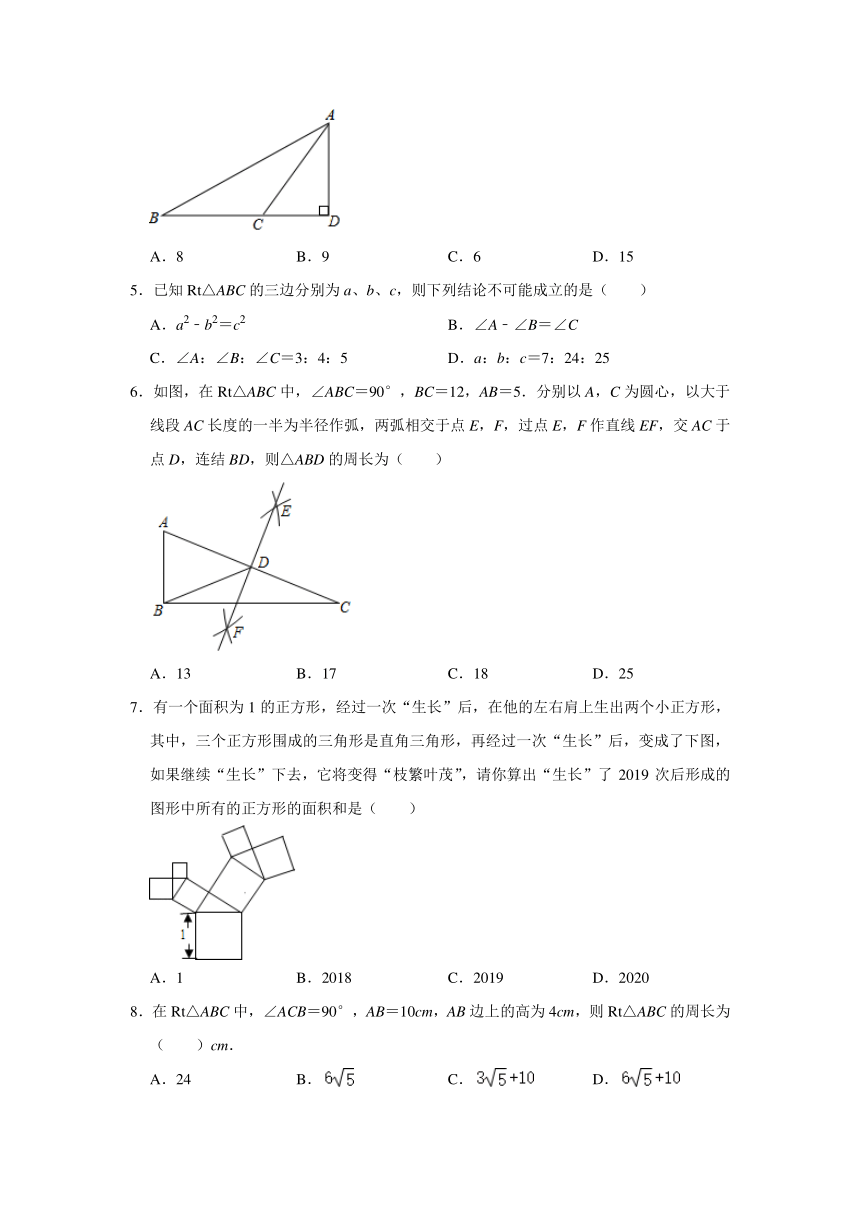
1.如图,在平面直角坐标系中,已知点A(﹣2,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的正半轴于点C,则点C的横坐标介于( )
A.0和1之间 B.1和2之间 C.2和3之间 D.3和4之间
2.如图,已知由16个边长为1的小正方形拼成的图案中,有五条线段PA、PB、PC、PD、PE,其中长度是有理数的有( )
A.1条 B.2条 C.3条 D.4条
3.如图,在等腰三角形ABC中,AC=BC=5,AB=8,D为底边上一动点(不与点A,B重合),DE⊥AC,DF⊥BC,垂足分别为E、F,则DE+DF=( )
A.5 B.8 C.13 D.4.8
4.如图△ABD中,∠D=90°,C是BD上一点,已知CB=9,AB=17,AD=8,则DC的长是( )
A.8 B.9 C.6 D.15
5.已知Rt△ABC的三边分别为a、b、c,则下列结论不可能成立的是( )
A.a2﹣b2=c2 B.∠A﹣∠B=∠C
C.∠A:∠B:∠C=3:4:5 D.a:b:c=7:24:25
6.如图,在Rt△ABC中,∠ABC=90°,BC=12,AB=5.分别以A,C为圆心,以大于线段AC长度的一半为半径作弧,两弧相交于点E,F,过点E,F作直线EF,交AC于点D,连结BD,则△ABD的周长为( )
A.13 B.17 C.18 D.25
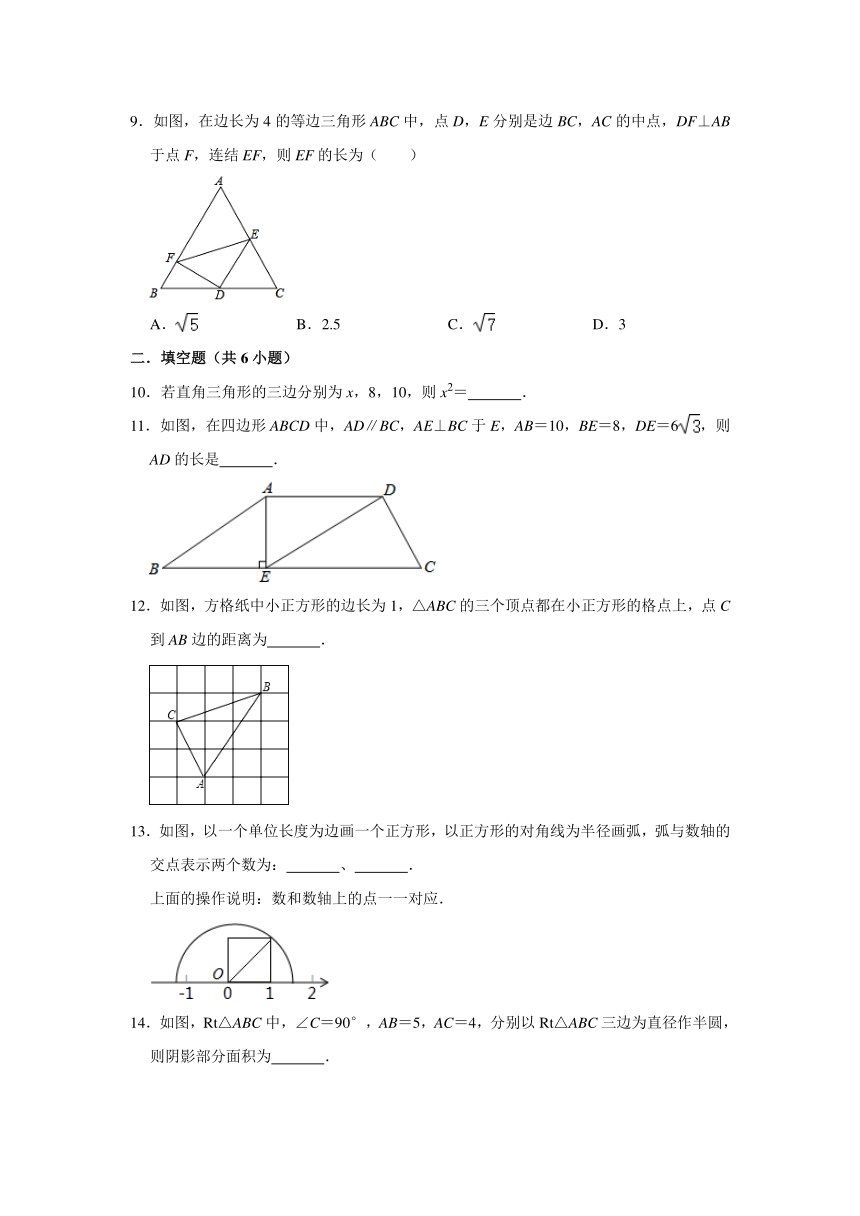
7.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是( )
A.1 B.2018 C.2019 D.2020
8.在Rt△ABC中,∠ACB=90°,AB=10cm,AB边上的高为4cm,则Rt△ABC的周长为( )cm.
A.24 B. C. D.
9.如图,在边长为4的等边三角形ABC中,点D,E分别是边BC,AC的中点,DF⊥AB于点F,连结EF,则EF的长为( )
A. B.2.5 C. D.3
二.填空题(共6小题)
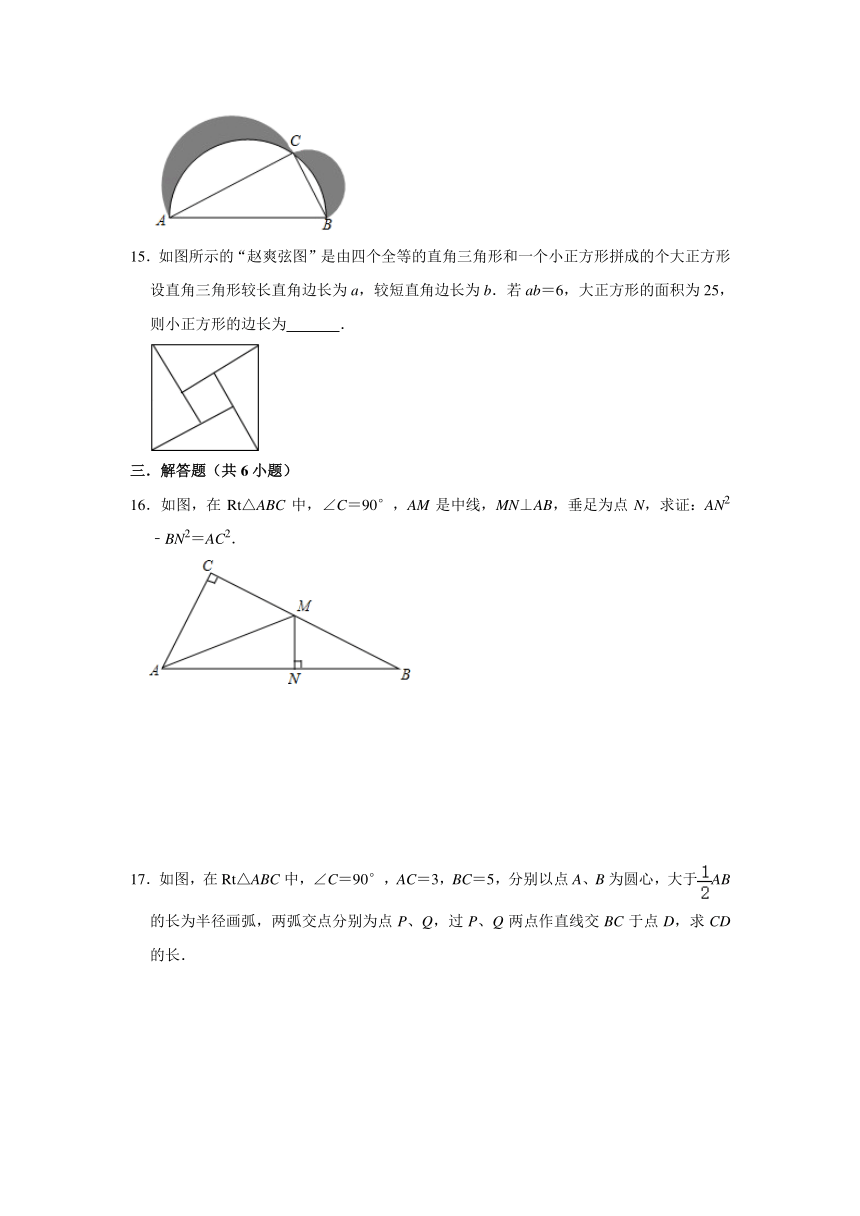
10.若直角三角形的三边分别为x,8,10,则x2= .
11.如图,在四边形ABCD中,AD∥BC,AE⊥BC于E,AB=10,BE=8,DE=6,则AD的长是 .
12.如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,点C到AB边的距离为 .
13.如图,以一个单位长度为边画一个正方形,以正方形的对角线为半径画弧,弧与数轴的交点表示两个数为: 、 .
上面的操作说明:数和数轴上的点一一对应.
14.如图,Rt△ABC中,∠C=90°,AB=5,AC=4,分别以Rt△ABC三边为直径作半圆,则阴影部分面积为 .
15.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的个大正方形设直角三角形较长直角边长为a,较短直角边长为b.若ab=6,大正方形的面积为25,则小正方形的边长为 .
三.解答题(共6小题)
16.如图,在Rt△ABC中,∠C=90°,AM是中线,MN⊥AB,垂足为点N,求证:AN2﹣BN2=AC2.
17.如图,在Rt△ABC中,∠C=90°,AC=3,BC=5,分别以点A、B为圆心,大于AB的长为半径画弧,两弧交点分别为点P、Q,过P、Q两点作直线交BC于点D,求CD的长.
18.如图,△ABC中,AB=4,∠ABC=45°,D是BC边上一点,且AD=AC,若BD﹣DC=1.求DC的长.
19.如图,在△ABC中,AB=AC,△ABC的高BH,CM交于点P.
(1)求证:PB=PC.
(2)若PB=5,PH=3,求AB.
20.如图,在四边形ABCD中,AB=AD=2,∠A=60°,BC2=20,CD=4,求∠ADC的度数.
21.利用如图4×4方格,每个小正方形的边长都为1.
(1)请求出图1中阴影正方形的面积与边长;
(2)请在图2中画出一个与图1中阴影部分面积不相等的正方形,要求它的边长为无理数,并求出它的边长;
(3)把分别表示图1与图2中的正方形的边长的实数在数轴上表示出来.
参考答案
一.选择题(共10小题)
1.【解答】解:∵点A,B的坐标分别为(﹣2,0),(0,3),
∴OA=2,OB=3,
在Rt△AOB中,由勾股定理得:AB==,
∴AC=AB=,
∴OC=﹣2,
∴点C的坐标为(﹣2,0),
∵,
∴,
即点C的横坐标介于1和2之间,
故选:B.
2.【解答】解:观察图形可知PA=4,
由勾股定理得:
PB==,
PC==5,
PD==2,
PE==,
故其中长度是有理数的有2条.
故选:B.
3.【解答】解:连接CD,过C点作底边AB上的高CG,
∵AC=BC=5,AB=8,
∴BG=4,CG===3,
∵S△ABC=S△ACD+S△DCB,
∴AB?CG=AC?DE+BC?DF,
∵AC=BC,
∴8×3=5×(DE+DF)
∴DE+DF=4.8.
故选:D.
4.【解答】解:∵△ABC中,∠D=90°,AB=17,AD=8,
∴BD===15,
∴DC=BD﹣CB=15﹣9=6.
故选:C.
5.【解答】解:(A)当∠A=90°时,此时a2=b2+c2,故A能成立.
(B)∵∠A=∠B+∠C,
∠A+∠B+∠C=180°,
∴∠A=90°,故B能成立.
(C)设∠A=3x,∠B=4x,∠C=5x,
∵∠A+∠B+∠C=180°,
∴x=15°,
∴∠C=75°,故C不能成立.
(D)设a=7x,b=24x,c=25x、
当∠C=90°,
∴a2+b2=c2,故D能成立,
故选:C.
6.【解答】解:∵∠ABC=90°,BC=12,AB=5,
∴AC==13,
根据题意可得EF是AC的垂直平分线,
∴D是AC的中点,
∴AD=AC=6.5,BD=AC=6.5,
∴△ABD的周长为6.5+6.5+5=18.
故选:C.
7.【解答】解:设直角三角形的是三条边分别是a,b,c.
根据勾股定理,得a2+b2=c2,
即正方形A的面积+正方形B的面积=正方形C的面积=1.
推而广之,“生长”了2019次后形成的图形中所有的正方形的面积和是2020×1=2020.
故选:D.
8.【解答】解:由勾股定理得,AC2+BC2=AB2=100,
由三角形的面积公式可知,?AC?BC=?AB?CD=20,
∴2?AC?BC=80
则(AC+BC)2=AC2+BC2+2?AC?BC=180,
解得,AC+BC=6,
∴Rt△ABC的周长=AC+BC+AB=6+10,
故选:D.
9.【解答】解:如图,在边长为4的等边三角形ABC中,点D,E分别是边BC,AC的中点,
∴AB=4,∠B=60°,BD=CD=2,DE是△ABC的中位线,
∴DE∥AB且DE=AB=2.
∵DF⊥AB,
∴∠DFB=90°,DF⊥DE,
∴∠BDF=30°,
∴BF=BD=1,
∴DF===.
在直角△DEF中,根据勾股定理得到:EF===.
故选:C.
二.填空题(共6小题)
10.【解答】解:分两种情况:
①两直角边分别为8,10,由勾股定理得x2=82+102=164,
②一直角边为8,斜边为10,由勾股定理得x2=102﹣82=36;
故答案为:36或164.
11.【解答】解:∵AE⊥BC,
∴∠AEB=90°,
∵AB=10,BE=8,
∴AE===6,
∵AD∥BC,
∴∠DAE=∠AEB=90°,
∴AD===6.
故答案为:6.
12.【解答】解:∵S△ABC=3×3﹣×1×2﹣×2×3﹣×1×3=,AB==,
∴点C到AB边的距离==.
故答案为:.
13.【解答】解:∵DO2=12+12=2,
∴DO=,
∵点A在1左边,点B在1右边.
∴点A表示的实数是1﹣,点B表示的实数是1+;
故答案是:1﹣,1+.
14.【解答】解:设别BC,AC,AB三边为直径的三个半圆面积分别表示为S1、S2、S3,
则有:S1=π()2=,
同理,S2=,S3=,
∵BC2+AC2=AB2,
∴S1+S2=S3;
∴S阴影=S1+S2+S△ABC﹣S3=S△ABC,
在直角△ABC中,BC==3,
则S阴影=S△ABC=AC?BC=×4×3=6.
故答案为6.
15.【解答】解:由题意可知:中间小正方形的边长为:a﹣b,
∵每一个直角三角形的面积为:ab=×6=3,
∴4×ab+(a﹣b)2=25,
∴(a﹣b)2=25﹣12=13,
∴a﹣b=,
故答案是:.
三.解答题(共6小题)
16.【解答】证明:∵MN⊥AB于N,
∴BN2=BM2﹣MN2,AN2=AM2﹣MN2
∴BN2﹣AN2=BM2﹣AM2,
又∵∠C=90°,
∴AM2=AC2+CM2
∴BN2﹣AN2=BM2﹣AC2﹣CM2,
又∵BM=CM,
∴BN2﹣AN2=﹣AC2,
即AN2﹣BN2=AC2.
17.【解答】解:连接AD.
∵PQ垂直平分线段AB,
∴DA=DB,设DA=DB=x,
在Rt△ACD中,∠C=90°,AD2=AC2+CD2,
∴x2=32+(5﹣x)2,
解得x=,
∴CD=BC﹣DB=5﹣=,
故答案为.
18.【解答】解:过点A作AE⊥BC于点E,如图所示.
∵AD=AC,AE⊥BC,
∴∠AEB=90°,DE=CE.
∵∠ABC=45°,
∴∠BAE=45°,
∴AE=BE.
在Rt△ABE中,AB=4,
∴AE2+BE2=AB2,即BE2+BE2=(4)2,
∴BE=4,
∴BD+DC=4.
又∵BD﹣DC=1,
∴DC+1+DC=4,
∴DC=2.
19.【解答】(1)证明:∵AB=AC,
∴∠ABC=∠ACB.
∵BH,CM为△ABC的高,
∴∠BMC=∠CHB=90°.
∴∠ABC+∠BCM=90°,∠ACB+∠CBH=90°.
∴∠BCM=∠CBH.
∴PB=PC.
(2)解:∵PB=PC,PB=5,
∴PC=5.
∵PH=3,∠CHB=90°,
∴CH=4.
设AB=x,则AH=x﹣4.
在Rt△ABH中,
∵AH 2+BH 2=AB 2,
∴(x﹣4) 2+(5+3) 2=x 2.
∴x=10.
即AB=10.
20.【解答】解:连接BD,
∵AB=AD=2,∠A=60°,
∴△ABD是等边三角形,
∴BD=2,∠ADB=60°,
∵BC2=20,CD=4,
则BD2+CD2=22+42=20,BC2=20,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=150°.
21.【解答】解(1)面积为4×4﹣4××1×3=10,
边长为;
(2)如图所示,正方形的边长为均可.(答案不唯一,合理即可.)
(3)表示或或的点如图所示.(答案不唯一,画出表示的点亦可)
