2019-2020学年九年级数学下册第27章圆达标检测卷含答案(新版)华东师大版(含答案)
文档属性
| 名称 | 2019-2020学年九年级数学下册第27章圆达标检测卷含答案(新版)华东师大版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 86.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 19:30:40 | ||
图片预览


文档简介
第27章达标检测卷
(120分,90分钟)
题 号 一 二 三 总 分
得 分
一、选择题(每题3分,共30分)
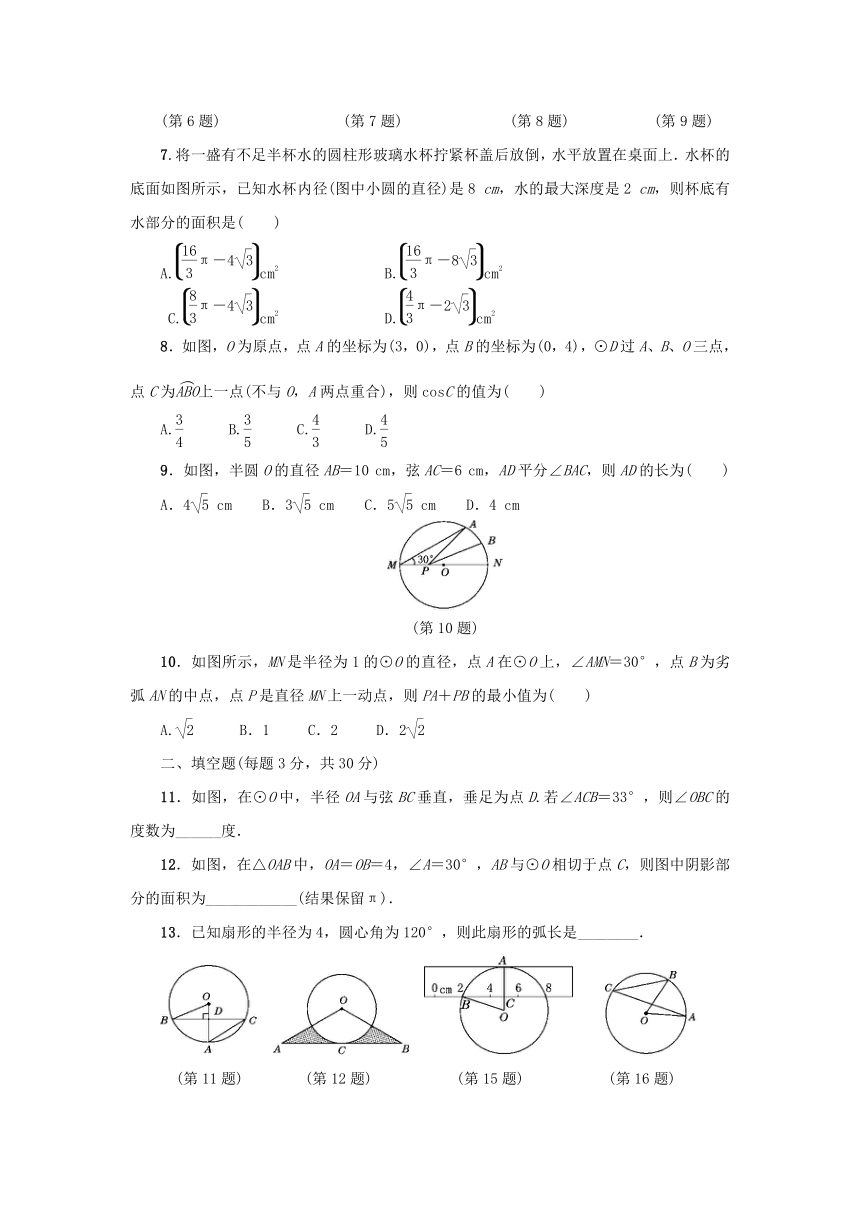
1.如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=20°,则∠C的度数是( )
A.70° B.50° C.45° D.20°
2.如图,在⊙O中,弦AB的长为8,OC⊥AB,垂足为C,且OC=3,则⊙O的半径为( )
A.5 B.10 C.8 D.6
(第1题) (第2题) (第3题) (第5题)
3.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠A=30°,则⊙O的半径是( )
A.1 B.2 C. D.
4.过⊙O内一点M的最长弦长为10 cm,最短弦长为8 cm,那么OM为( )
A.6 cm B.3 cm C.cm D.9 cm
5.如图,已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )
A.15° B.20° C.25° D.30°
6.如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与⊙O相切于点D,则下列结论中不一定正确的是( )
A.AG=BG B.AB∥EF C.AD∥BC D.∠ABC=∠ADC
(第6题) (第7题) (第8题) (第9题)
7.将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上.水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8 cm,水的最大深度是2 cm,则杯底有水部分的面积是( )
A.cm2 B.cm2
C.cm2 D.cm2
8.如图,O为原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A、B、O三点,点C为上一点(不与O,A两点重合),则cosC的值为( )
A. B. C. D.
9.如图,半圆O的直径AB=10 cm,弦AC=6 cm,AD平分∠BAC,则AD的长为( )
A.4 cm B.3 cm C.5 cm D.4 cm
(第10题)
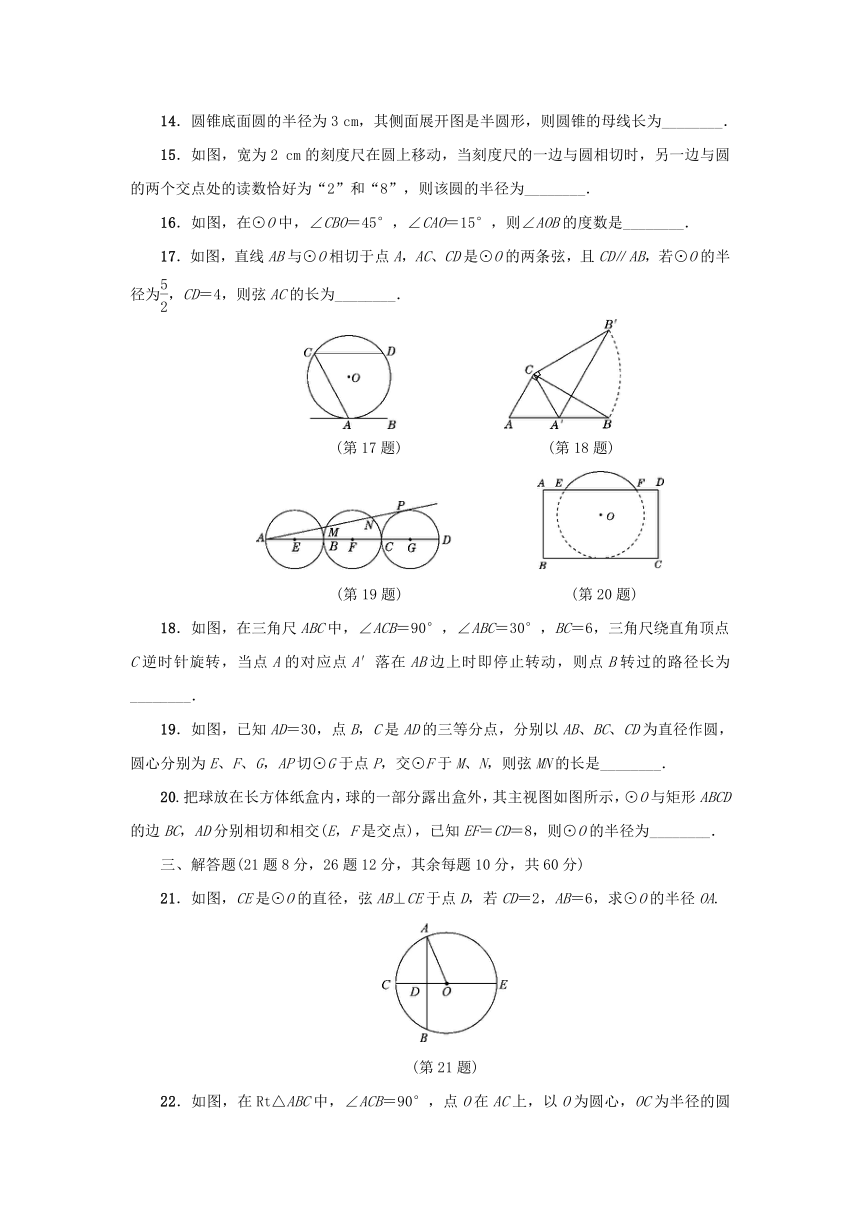
10.如图所示,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点,点P是直径MN上一动点,则PA+PB的最小值为( )
A. B.1 C.2 D.2
二、填空题(每题3分,共30分)
11.如图,在⊙O中,半径OA与弦BC垂直,垂足为点D.若∠ACB=33°,则∠OBC的度数为______度.
12.如图,在△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,则图中阴影部分的面积为____________(结果保留π).
13.已知扇形的半径为4,圆心角为120°,则此扇形的弧长是________.
(第11题) (第12题) (第15题) (第16题)
14.圆锥底面圆的半径为3 cm,其侧面展开图是半圆形,则圆锥的母线长为________.
15.如图,宽为2 cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数恰好为“2”和“8”,则该圆的半径为________.
16.如图,在⊙O中,∠CBO=45°,∠CAO=15°,则∠AOB的度数是________.
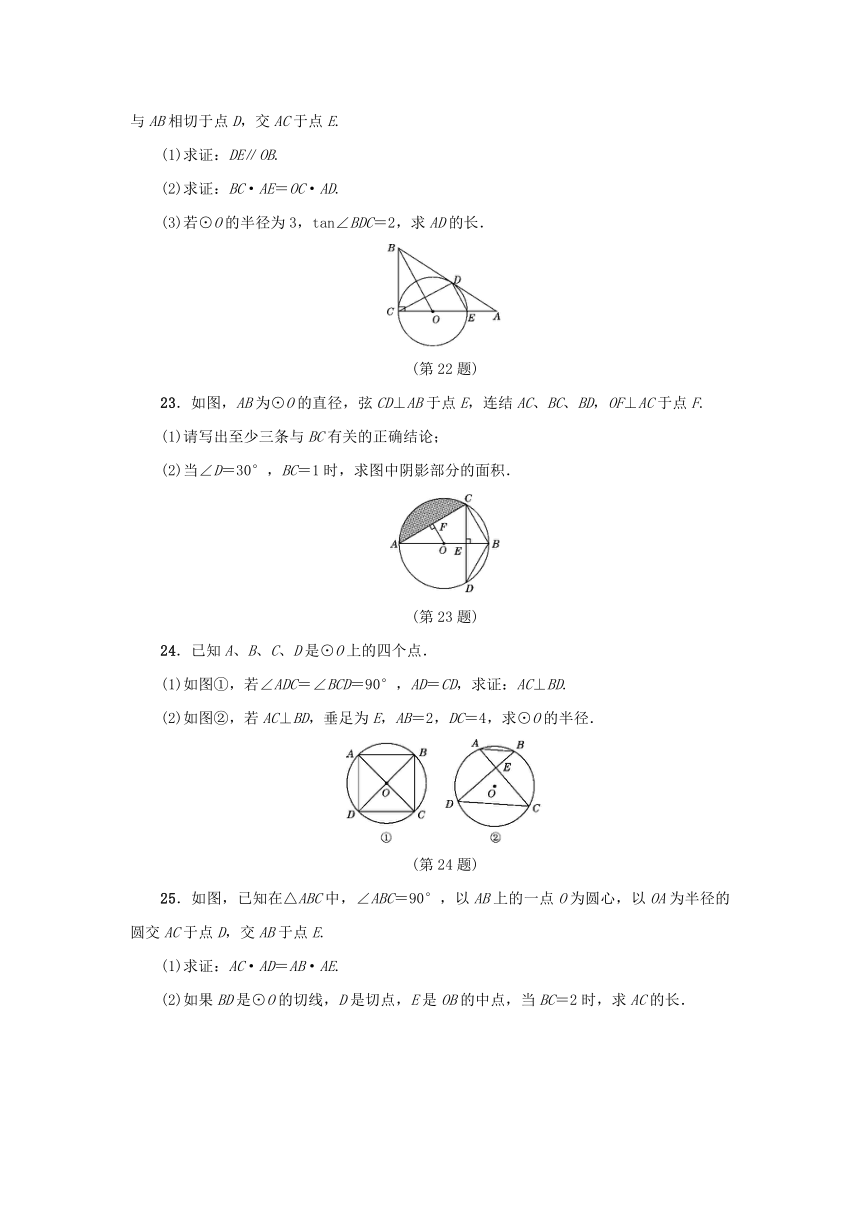
17.如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为,CD=4,则弦AC的长为________.
(第17题) (第18题)
(第19题) (第20题)
18.如图,在三角尺ABC中,∠ACB=90°,∠ABC=30°,BC=6,三角尺绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边上时即停止转动,则点B转过的路径长为________.
19.如图,已知AD=30,点B,C是AD的三等分点,分别以AB、BC、CD为直径作圆,圆心分别为E、F、G,AP切⊙G于点P,交⊙F于M、N,则弦MN的长是________.
20.把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图所示,⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为________.
三、解答题(21题8分,26题12分,其余每题10分,共60分)
21.如图,CE是⊙O的直径,弦AB⊥CE于点D,若CD=2,AB=6,求⊙O的半径OA.
(第21题)
22.如图,在Rt△ABC中,∠ACB=90°,点O在AC上,以O为圆心,OC为半径的圆与AB相切于点D,交AC于点E.
(1)求证:DE∥OB.
(2)求证:BC·AE=OC·AD.
(3)若⊙O的半径为3,tan∠BDC=2,求AD的长.
(第22题)
23.如图,AB为⊙O的直径,弦CD⊥AB于点E,连结AC、BC、BD,OF⊥AC于点F.
(1)请写出至少三条与BC有关的正确结论;
(2)当∠D=30°,BC=1时,求图中阴影部分的面积.
(第23题)
24.已知A、B、C、D是⊙O上的四个点.
(1)如图①,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD.
(2)如图②,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.
(第24题)
25.如图,已知在△ABC中,∠ABC=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
(1)求证:AC·AD=AB·AE.
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
(第25题)
26.如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴相交于点C,直线l对应的函数表达式为y=x+4,与x轴相交于点D,以C为顶点的抛物线经过点B.
(1)求抛物线对应的函数表达式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3)动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.
(第26题)
参考答案
一、1.B
2.A 点拨:连结OA,∵OC⊥AB,∴AC=BC=AB=4.
在Rt△OAC中,由勾股定理得OA===5.
3.A 点拨:本题运用数形结合思想,如图,过B作直径BB′,连结B′C,则∠B′=30°,∠B′CB=90°,∴BC=B′B,则B′B=2×1=2,故⊙O的半径为1.
(第3题)
4.B
5.B 点拨:连结OC,则∠AOC=110°,则∠P=110°-90°=20°.
6.C 点拨:∵EF是⊙O的切线,∴EF⊥CD,∴AB∥EF.根据垂径定理得AG=GB,再根据同弧所对的圆周角相等得∠ADC=∠ABC.
7.A
8.D 点拨:本题运用数形结合思想,连结AB,如图所示,易知AB为⊙D的直径,由勾股定理得AB==5,由同弧所对的圆周角相等,得∠C=∠OBA.在Rt△OAB中,cos∠OBA==.
(第8题)
9.A 点拨:如图,连结BD并延长,交AC的延长线于点E,连结BC,则∠ACB=90°,∠ADB=90°.又∵AB=10 cm,AC=6 cm,∴BC=8 cm.∵∠BAD=∠EAD,AD=AD,∠ADB=∠ADE=90°,∴△ADB≌△ADE,∴AE=AB=10 cm,BD=ED,∴CE=4 cm.∵∠ACB=90°,∴∠BCE=90°.∴BD=BE==2(cm),∴AD===4(cm).故选A.
(第9题)
10.A 点拨:如图,作点B关于MN的对称点B′,连结OA,OB,OB′,AB′,则AB′与MN的交点P′即为使PA+PB最小时的点,PA+PB的最小值=AB′.∵∠AMN=30°,∴∠AON=2∠AMN=2×30°=60°,∵点B为劣弧AN的中点,∴∠BON=∠AON=×60°=30°,由对称性知∠B′ON=∠BON=30°,∴∠AOB′=∠AON+∠B′ON=60°+30°=90°,∴△AOB′为等腰直角三角形,∴AB′=OA=×1=,即PA+PB的最小值为.故选A.
(第10题)
二、11.24
12.4-π 点拨:连结OC,则OC⊥AB.∵∠A=30°,∴∠AOC=60°.∵OA=OB,∴∠AOB=2∠AOC=120°.在Rt△AOC中,OC=OA=2,∴AC==2,∴AB=2AC=4,∴S△AOB=AB·OC=4,S扇形=π·22=π,∴S阴影=S△AOB-S扇形=4-π.
13.π 点拨:弧长为=π.
14.6 cm
15. cm 点拨:本题运用数形结合思想和方程思想,设半径为R cm,则OC=(R-2)cm,在Rt△OBC中,由勾股定理得BO2=OC2+BC2,即R2=(R-2)2+32,解得R=.
16.60° 点拨:连结OC,则∠OCB=45°,∠OCA=15°,所以∠ACB=30°.根据同弧所对的圆周角等于圆心角的一半,知∠AOB=60°.
17.2 点拨:连结AO并延长交CD于点E.连结OD.∵AB是⊙O的切线,∴EA⊥AB.又∵CD∥AB,∴AE⊥CD,∴CE=ED=2.在Rt△OED中,OE==,∴AE=+=4.在Rt△ACE中,AC==2.
18.2π 点拨:在△ABC中,∠ACB=90°,∠ABC=30°,则∠A=60°,由旋转知AC=A′C,∴△AA′C是等边三角形,∴旋转角∠ACA′=60°,则∠BCB′=60°,故点B转过的路径长为=2π.
19.8 点拨:连结GP,FN,过F作FH⊥MN,垂足为H,则△AFH∽△AGP,∴=,即=.则FH=3.HN===4,∴MN=2HN=8.
20.5 点拨:如图,设⊙O与BC相切于点G,作直线OG,分别交AD,劣弧EF于点H,I,再连结OF.在矩形ABCD中,AD∥BC,而IG⊥BC,∴IG⊥AD,∴FH=EF=4,设球的半径为r,则OH=8-r.在Rt△OFH中,r2-(8-r)2=42,解得r=5.
(第20题)
三、21.解:∵CE为⊙O的直径,AB⊥CE,∴AD=AB=3.
又CD=2,∴OD=OC-CD=OA-2.
OA2-OD2=AD2,即OA2-(OA-2)2=32,
∴OA=.
22.(1)证明:设OB与CD交于F.因为CE是⊙O的直径,所以∠EDC=90°.
又因为BC⊥AC,所以BC是⊙O的切线.
因为AB是⊙O的切线,所以BC=BD,∠CBF=∠DBF,
所以OB⊥CD,即∠CFO=90°.
所以∠CFO=∠EDC=90°,所以DE∥OB.
(2)证明:因为OB∥DE,
所以=.
又因为BD=BC,
OC=OE,所以=,
即BC·AE=OC·AD.
(3)解:因为BD=BC,
所以∠BDC=∠BCD.
因为∠BCO=∠CFO=90°,
所以∠BOC=∠BCD,
所以∠BOC=∠BDC.
所以BC=OC·tan∠BOC=3·tan∠BDC=3×2=6.
设AD=x.由(2)得6·AE=3x,
所以AE=.
在Rt△BCA中,有BC2+AC2=AB2,即62+=(6+x)2.
解得x1=4,x2=-12(舍去),所以AD=4.
23.解:(1)①BC=BD;②OF∥BC;③OF=BC;④BC⊥AC;⑤BC2=BE·AB;⑥BC2=CE2+BE2等.
(2)连结OC,则OC=OA=OB,∵∠D=30°,∴∠A=∠D=30°,∴∠AOC=120°.∵AB是⊙O的直径,
∴∠ACB=90°.在Rt△ABC中,∠A=30°,BC=1,∴AB=2,AC=.∵OF⊥AC,∴AF=CF.又∵OA=OB,∴OF是△ABC的中位线,∴OF=BC=,∴S△AOC=AC·OF=××=,S扇形OAC=π×OA2=,∴S阴影=S扇形OAC-S△AOC=-.
24.(1)证明:∵∠ADC=∠BCD=90°,∴AC、BD是⊙O的直径,∴∠DAB=∠ABC=90°,∴四边形ABCD是矩形.∵AD=CD,∴四边形ABCD是正方形,∴AC⊥BD.
(第24题)
(2)解:如图,作直径DF,连结CF、BF.∵DF是直径,∴∠DCF=∠DBF=90°,∴FB⊥DB.又∵AC⊥BD,∴BF∥AC,∴=,∴CF=AB.根据勾股定理,得DF2=CF2+DC2=AB2+DC2=20,∴DF=2,∴OD=,即⊙O的半径为.
25.(1)证明:如图,连结DE,
∵AE是⊙O的直径,
∴∠ADE=90°.
∴∠ADE=∠ABC.
在Rt△ADE和Rt△ABC中,∠A是公共角,
∴△ADE∽△ABC.
∴=,即AC·AD=AB·AE.
(第25题)
(2)解:如图,连结OD,
∵BD是⊙O的切线,∴OD⊥BD.
在Rt△OBD中,OE=BE=OD,
∴OB=2OD,∴∠OBD=30°.
易知∠BAC=30°.
在Rt△ABC中,AC=2BC=2×2=4.
26.解:(1)如图,连结AE.
由已知,得AE=CE=5,OE=3.
在Rt△AOE中,由勾股定理得,
OA===4.
∵OC⊥AB,∴由垂径定理,得OB=OA=4.
又∵OC=OE+CE=3+5=8.
∴B(0,-4),C(8,0).
∵抛物线的顶点为点C,
∴设抛物线对应的函数表达式为y=a(x-8)2.
将点B的坐标代入,得
64a=-4.a=-.
∴y=-(x-8)2.
∴y=-x2+x-4为所求抛物线对应的函数表达式.
(第26题)
(2)直线l与⊙E相切.理由如下:
在直线l对应的函数表达式y=x+4中,令y=0,得x+4=0,解得x=-,
∴点D的坐标为;
当x=0时,y=4,又易知A(0,4),∴点A在直线l上.
在Rt△AOE和Rt△DOA中,
∵=,=,∴=.
∵∠AOE=∠DOA=90°,
∴△AOE∽△DOA.
∴∠AEO=∠DAO.
∵∠AEO+∠EAO=90°,
∴∠DAO+∠EAO=90°,
即∠DAE=90°.
因此,直线l与⊙E相切.
(3)如图,过点P作直线l的垂线段PQ,垂足为Q;过点P作直线PM垂直于x轴,交直线l于点M.
设M,P.则
PM=m+4-=m2-m+8=(m-2)2+.
当m=2时,PM取得最小值.
此时,P.
对于△PQM,∵PM⊥x轴,
∴∠QMP=∠DAO=∠AEO.
又∵∠PQM=90°,
∴△PQM的三个内角固定不变.
∴在动点P运动的过程中,△PQM的三边的比例关系不变.
∴当PM取得最小值时,PQ也取得最小值.
PQ最小=PM最小·sin∠QMP=PM最小·sin∠AEO=×=.
所以,当抛物线上的动点P的坐标为时,点P到直线l的距离最小,其最小距离为.
(120分,90分钟)
题 号 一 二 三 总 分
得 分
一、选择题(每题3分,共30分)
1.如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=20°,则∠C的度数是( )
A.70° B.50° C.45° D.20°
2.如图,在⊙O中,弦AB的长为8,OC⊥AB,垂足为C,且OC=3,则⊙O的半径为( )
A.5 B.10 C.8 D.6
(第1题) (第2题) (第3题) (第5题)
3.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠A=30°,则⊙O的半径是( )
A.1 B.2 C. D.
4.过⊙O内一点M的最长弦长为10 cm,最短弦长为8 cm,那么OM为( )
A.6 cm B.3 cm C.cm D.9 cm
5.如图,已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )
A.15° B.20° C.25° D.30°
6.如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与⊙O相切于点D,则下列结论中不一定正确的是( )
A.AG=BG B.AB∥EF C.AD∥BC D.∠ABC=∠ADC
(第6题) (第7题) (第8题) (第9题)
7.将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上.水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8 cm,水的最大深度是2 cm,则杯底有水部分的面积是( )
A.cm2 B.cm2
C.cm2 D.cm2
8.如图,O为原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A、B、O三点,点C为上一点(不与O,A两点重合),则cosC的值为( )
A. B. C. D.
9.如图,半圆O的直径AB=10 cm,弦AC=6 cm,AD平分∠BAC,则AD的长为( )
A.4 cm B.3 cm C.5 cm D.4 cm
(第10题)
10.如图所示,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点,点P是直径MN上一动点,则PA+PB的最小值为( )
A. B.1 C.2 D.2
二、填空题(每题3分,共30分)
11.如图,在⊙O中,半径OA与弦BC垂直,垂足为点D.若∠ACB=33°,则∠OBC的度数为______度.
12.如图,在△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,则图中阴影部分的面积为____________(结果保留π).
13.已知扇形的半径为4,圆心角为120°,则此扇形的弧长是________.
(第11题) (第12题) (第15题) (第16题)
14.圆锥底面圆的半径为3 cm,其侧面展开图是半圆形,则圆锥的母线长为________.
15.如图,宽为2 cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数恰好为“2”和“8”,则该圆的半径为________.
16.如图,在⊙O中,∠CBO=45°,∠CAO=15°,则∠AOB的度数是________.
17.如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为,CD=4,则弦AC的长为________.
(第17题) (第18题)
(第19题) (第20题)
18.如图,在三角尺ABC中,∠ACB=90°,∠ABC=30°,BC=6,三角尺绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边上时即停止转动,则点B转过的路径长为________.
19.如图,已知AD=30,点B,C是AD的三等分点,分别以AB、BC、CD为直径作圆,圆心分别为E、F、G,AP切⊙G于点P,交⊙F于M、N,则弦MN的长是________.
20.把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图所示,⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为________.
三、解答题(21题8分,26题12分,其余每题10分,共60分)
21.如图,CE是⊙O的直径,弦AB⊥CE于点D,若CD=2,AB=6,求⊙O的半径OA.
(第21题)
22.如图,在Rt△ABC中,∠ACB=90°,点O在AC上,以O为圆心,OC为半径的圆与AB相切于点D,交AC于点E.
(1)求证:DE∥OB.
(2)求证:BC·AE=OC·AD.
(3)若⊙O的半径为3,tan∠BDC=2,求AD的长.
(第22题)
23.如图,AB为⊙O的直径,弦CD⊥AB于点E,连结AC、BC、BD,OF⊥AC于点F.
(1)请写出至少三条与BC有关的正确结论;
(2)当∠D=30°,BC=1时,求图中阴影部分的面积.
(第23题)
24.已知A、B、C、D是⊙O上的四个点.
(1)如图①,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD.
(2)如图②,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.
(第24题)
25.如图,已知在△ABC中,∠ABC=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
(1)求证:AC·AD=AB·AE.
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
(第25题)
26.如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴相交于点C,直线l对应的函数表达式为y=x+4,与x轴相交于点D,以C为顶点的抛物线经过点B.
(1)求抛物线对应的函数表达式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3)动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.
(第26题)
参考答案
一、1.B
2.A 点拨:连结OA,∵OC⊥AB,∴AC=BC=AB=4.
在Rt△OAC中,由勾股定理得OA===5.
3.A 点拨:本题运用数形结合思想,如图,过B作直径BB′,连结B′C,则∠B′=30°,∠B′CB=90°,∴BC=B′B,则B′B=2×1=2,故⊙O的半径为1.
(第3题)
4.B
5.B 点拨:连结OC,则∠AOC=110°,则∠P=110°-90°=20°.
6.C 点拨:∵EF是⊙O的切线,∴EF⊥CD,∴AB∥EF.根据垂径定理得AG=GB,再根据同弧所对的圆周角相等得∠ADC=∠ABC.
7.A
8.D 点拨:本题运用数形结合思想,连结AB,如图所示,易知AB为⊙D的直径,由勾股定理得AB==5,由同弧所对的圆周角相等,得∠C=∠OBA.在Rt△OAB中,cos∠OBA==.
(第8题)
9.A 点拨:如图,连结BD并延长,交AC的延长线于点E,连结BC,则∠ACB=90°,∠ADB=90°.又∵AB=10 cm,AC=6 cm,∴BC=8 cm.∵∠BAD=∠EAD,AD=AD,∠ADB=∠ADE=90°,∴△ADB≌△ADE,∴AE=AB=10 cm,BD=ED,∴CE=4 cm.∵∠ACB=90°,∴∠BCE=90°.∴BD=BE==2(cm),∴AD===4(cm).故选A.
(第9题)
10.A 点拨:如图,作点B关于MN的对称点B′,连结OA,OB,OB′,AB′,则AB′与MN的交点P′即为使PA+PB最小时的点,PA+PB的最小值=AB′.∵∠AMN=30°,∴∠AON=2∠AMN=2×30°=60°,∵点B为劣弧AN的中点,∴∠BON=∠AON=×60°=30°,由对称性知∠B′ON=∠BON=30°,∴∠AOB′=∠AON+∠B′ON=60°+30°=90°,∴△AOB′为等腰直角三角形,∴AB′=OA=×1=,即PA+PB的最小值为.故选A.
(第10题)
二、11.24
12.4-π 点拨:连结OC,则OC⊥AB.∵∠A=30°,∴∠AOC=60°.∵OA=OB,∴∠AOB=2∠AOC=120°.在Rt△AOC中,OC=OA=2,∴AC==2,∴AB=2AC=4,∴S△AOB=AB·OC=4,S扇形=π·22=π,∴S阴影=S△AOB-S扇形=4-π.
13.π 点拨:弧长为=π.
14.6 cm
15. cm 点拨:本题运用数形结合思想和方程思想,设半径为R cm,则OC=(R-2)cm,在Rt△OBC中,由勾股定理得BO2=OC2+BC2,即R2=(R-2)2+32,解得R=.
16.60° 点拨:连结OC,则∠OCB=45°,∠OCA=15°,所以∠ACB=30°.根据同弧所对的圆周角等于圆心角的一半,知∠AOB=60°.
17.2 点拨:连结AO并延长交CD于点E.连结OD.∵AB是⊙O的切线,∴EA⊥AB.又∵CD∥AB,∴AE⊥CD,∴CE=ED=2.在Rt△OED中,OE==,∴AE=+=4.在Rt△ACE中,AC==2.
18.2π 点拨:在△ABC中,∠ACB=90°,∠ABC=30°,则∠A=60°,由旋转知AC=A′C,∴△AA′C是等边三角形,∴旋转角∠ACA′=60°,则∠BCB′=60°,故点B转过的路径长为=2π.
19.8 点拨:连结GP,FN,过F作FH⊥MN,垂足为H,则△AFH∽△AGP,∴=,即=.则FH=3.HN===4,∴MN=2HN=8.
20.5 点拨:如图,设⊙O与BC相切于点G,作直线OG,分别交AD,劣弧EF于点H,I,再连结OF.在矩形ABCD中,AD∥BC,而IG⊥BC,∴IG⊥AD,∴FH=EF=4,设球的半径为r,则OH=8-r.在Rt△OFH中,r2-(8-r)2=42,解得r=5.
(第20题)
三、21.解:∵CE为⊙O的直径,AB⊥CE,∴AD=AB=3.
又CD=2,∴OD=OC-CD=OA-2.
OA2-OD2=AD2,即OA2-(OA-2)2=32,
∴OA=.
22.(1)证明:设OB与CD交于F.因为CE是⊙O的直径,所以∠EDC=90°.
又因为BC⊥AC,所以BC是⊙O的切线.
因为AB是⊙O的切线,所以BC=BD,∠CBF=∠DBF,
所以OB⊥CD,即∠CFO=90°.
所以∠CFO=∠EDC=90°,所以DE∥OB.
(2)证明:因为OB∥DE,
所以=.
又因为BD=BC,
OC=OE,所以=,
即BC·AE=OC·AD.
(3)解:因为BD=BC,
所以∠BDC=∠BCD.
因为∠BCO=∠CFO=90°,
所以∠BOC=∠BCD,
所以∠BOC=∠BDC.
所以BC=OC·tan∠BOC=3·tan∠BDC=3×2=6.
设AD=x.由(2)得6·AE=3x,
所以AE=.
在Rt△BCA中,有BC2+AC2=AB2,即62+=(6+x)2.
解得x1=4,x2=-12(舍去),所以AD=4.
23.解:(1)①BC=BD;②OF∥BC;③OF=BC;④BC⊥AC;⑤BC2=BE·AB;⑥BC2=CE2+BE2等.
(2)连结OC,则OC=OA=OB,∵∠D=30°,∴∠A=∠D=30°,∴∠AOC=120°.∵AB是⊙O的直径,
∴∠ACB=90°.在Rt△ABC中,∠A=30°,BC=1,∴AB=2,AC=.∵OF⊥AC,∴AF=CF.又∵OA=OB,∴OF是△ABC的中位线,∴OF=BC=,∴S△AOC=AC·OF=××=,S扇形OAC=π×OA2=,∴S阴影=S扇形OAC-S△AOC=-.
24.(1)证明:∵∠ADC=∠BCD=90°,∴AC、BD是⊙O的直径,∴∠DAB=∠ABC=90°,∴四边形ABCD是矩形.∵AD=CD,∴四边形ABCD是正方形,∴AC⊥BD.
(第24题)
(2)解:如图,作直径DF,连结CF、BF.∵DF是直径,∴∠DCF=∠DBF=90°,∴FB⊥DB.又∵AC⊥BD,∴BF∥AC,∴=,∴CF=AB.根据勾股定理,得DF2=CF2+DC2=AB2+DC2=20,∴DF=2,∴OD=,即⊙O的半径为.
25.(1)证明:如图,连结DE,
∵AE是⊙O的直径,
∴∠ADE=90°.
∴∠ADE=∠ABC.
在Rt△ADE和Rt△ABC中,∠A是公共角,
∴△ADE∽△ABC.
∴=,即AC·AD=AB·AE.
(第25题)
(2)解:如图,连结OD,
∵BD是⊙O的切线,∴OD⊥BD.
在Rt△OBD中,OE=BE=OD,
∴OB=2OD,∴∠OBD=30°.
易知∠BAC=30°.
在Rt△ABC中,AC=2BC=2×2=4.
26.解:(1)如图,连结AE.
由已知,得AE=CE=5,OE=3.
在Rt△AOE中,由勾股定理得,
OA===4.
∵OC⊥AB,∴由垂径定理,得OB=OA=4.
又∵OC=OE+CE=3+5=8.
∴B(0,-4),C(8,0).
∵抛物线的顶点为点C,
∴设抛物线对应的函数表达式为y=a(x-8)2.
将点B的坐标代入,得
64a=-4.a=-.
∴y=-(x-8)2.
∴y=-x2+x-4为所求抛物线对应的函数表达式.
(第26题)
(2)直线l与⊙E相切.理由如下:
在直线l对应的函数表达式y=x+4中,令y=0,得x+4=0,解得x=-,
∴点D的坐标为;
当x=0时,y=4,又易知A(0,4),∴点A在直线l上.
在Rt△AOE和Rt△DOA中,
∵=,=,∴=.
∵∠AOE=∠DOA=90°,
∴△AOE∽△DOA.
∴∠AEO=∠DAO.
∵∠AEO+∠EAO=90°,
∴∠DAO+∠EAO=90°,
即∠DAE=90°.
因此,直线l与⊙E相切.
(3)如图,过点P作直线l的垂线段PQ,垂足为Q;过点P作直线PM垂直于x轴,交直线l于点M.
设M,P.则
PM=m+4-=m2-m+8=(m-2)2+.
当m=2时,PM取得最小值.
此时,P.
对于△PQM,∵PM⊥x轴,
∴∠QMP=∠DAO=∠AEO.
又∵∠PQM=90°,
∴△PQM的三个内角固定不变.
∴在动点P运动的过程中,△PQM的三边的比例关系不变.
∴当PM取得最小值时,PQ也取得最小值.
PQ最小=PM最小·sin∠QMP=PM最小·sin∠AEO=×=.
所以,当抛物线上的动点P的坐标为时,点P到直线l的距离最小,其最小距离为.
