圆锥曲线与方程复习课件17张PPT
文档属性
| 名称 | 圆锥曲线与方程复习课件17张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-13 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
圆锥曲线定义:
(一)
圆
锥
曲
线
椭圆
双曲线
抛物线
定义
标准方程
几何性质
知识回顾(二)
双曲线的定义:
平面内到两个定点F1、F2的距离和等于常数 (大于F1F2 )的点的轨迹叫做椭圆。
(二)
可用表达式 表示。
平面内到两个定点F1、F2距离差的绝对值等于
常数(小于F1F2 )的点的轨迹叫做双曲线。
可用表达式 表示。
抛物线的定义:
平面内到一个定点F和一条定直线 l(F不在l上)
的距离相等的点的轨迹叫做抛物线.
可用表达式 MF=d 表示,其中d为F到l的距离.
椭圆的定义:
(三)
椭圆的标准方程:
双曲线的标准方程:
抛物线的标准方程:
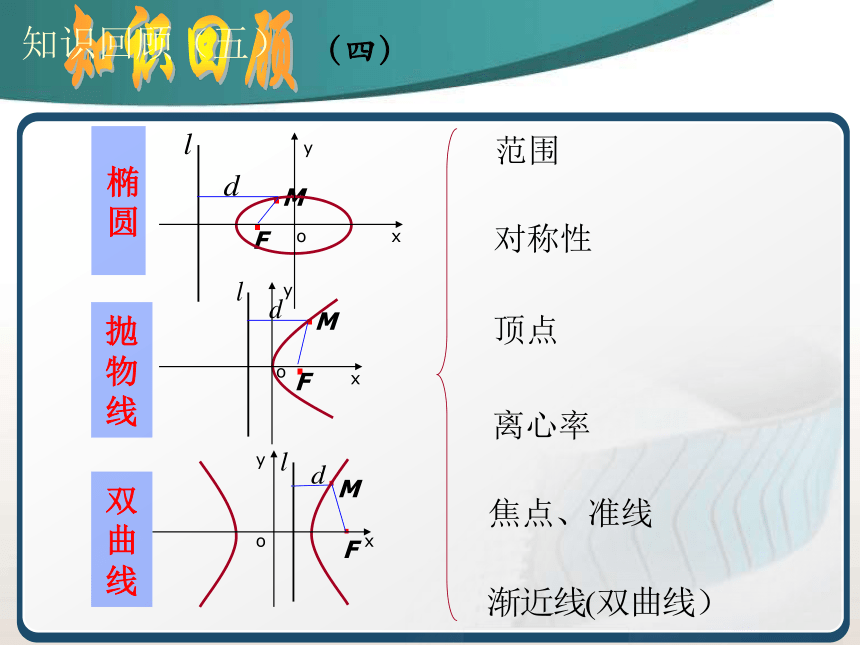
知识回顾(四)
(四)
椭
圆
抛
物
线
双
曲
线
知识回顾(五)
y
x
o
y
x
o
y
x
o
【核心解读】
1.椭圆中的特征三角形
a2=c2+b2,a>b>0,a最大,其中a,b,c构成
如图的直角三角形,我们把它称作“特
征三角形”.
2.双曲线渐近线的设法技巧
(1)由双曲线标准方程求其渐近线方程时,最简单实用的办法
是:把标准方程中的1换成0,即可得到两条渐近线的方程.如
双曲线 (a>0,b>0)的渐近线方程为 (a>
0,b>0),即 双曲线 (a>0,b>0)的渐近线方
程为 (a>0,b>0),即
(2)如果双曲线的渐近线为 时,它的双曲线方程可设
为 (λ≠0).
3.抛物线的焦点弦问题
抛物线过焦点F的弦长|AB|的一个重要结论.
(1)y2=2px(p>0)中,|AB|=x1+x2+p.
(2)y2=-2px(p>0)中,|AB|=-x1-x2+p.
(3)x2=2py(p>0)中,|AB|=y1+y2+p.
(4)x2=-2py(p>0)中,|AB|=-y1-y2+p.
基础训练
基础训练1、2、3
基础训练
基础训练4、5、6
4
(0,-1)
典型例题
典型例题1
【例1】
已知椭圆的中心在原点,焦点在坐标轴上,又过点
P(3,2),长轴长是短轴长的3倍,求该椭圆的方程。
解:由题知,椭圆的方程为标准方程。
小结:本题用待定系数法求椭圆的标准方程,
但在无法判断焦点所在的坐标轴时,要分情况讨论
历年真题
历年真题
历年真题
历年真题
课堂小结
本节课主要复习圆锥曲线的定义、标准方程、
几何性质及应用,同时注重与其他知识的综合
运用,在解题时除了要熟练掌握圆锥曲线基本知
识外,需注重利用数形结合思想解决实际问题。
课堂小结
圆锥曲线定义:
(一)
圆
锥
曲
线
椭圆
双曲线
抛物线
定义
标准方程
几何性质
知识回顾(二)
双曲线的定义:
平面内到两个定点F1、F2的距离和等于常数 (大于F1F2 )的点的轨迹叫做椭圆。
(二)
可用表达式 表示。
平面内到两个定点F1、F2距离差的绝对值等于
常数(小于F1F2 )的点的轨迹叫做双曲线。
可用表达式 表示。
抛物线的定义:
平面内到一个定点F和一条定直线 l(F不在l上)
的距离相等的点的轨迹叫做抛物线.
可用表达式 MF=d 表示,其中d为F到l的距离.
椭圆的定义:
(三)
椭圆的标准方程:
双曲线的标准方程:
抛物线的标准方程:
知识回顾(四)
(四)
椭
圆
抛
物
线
双
曲
线
知识回顾(五)
y
x
o
y
x
o
y
x
o
【核心解读】
1.椭圆中的特征三角形
a2=c2+b2,a>b>0,a最大,其中a,b,c构成
如图的直角三角形,我们把它称作“特
征三角形”.
2.双曲线渐近线的设法技巧
(1)由双曲线标准方程求其渐近线方程时,最简单实用的办法
是:把标准方程中的1换成0,即可得到两条渐近线的方程.如
双曲线 (a>0,b>0)的渐近线方程为 (a>
0,b>0),即 双曲线 (a>0,b>0)的渐近线方
程为 (a>0,b>0),即
(2)如果双曲线的渐近线为 时,它的双曲线方程可设
为 (λ≠0).
3.抛物线的焦点弦问题
抛物线过焦点F的弦长|AB|的一个重要结论.
(1)y2=2px(p>0)中,|AB|=x1+x2+p.
(2)y2=-2px(p>0)中,|AB|=-x1-x2+p.
(3)x2=2py(p>0)中,|AB|=y1+y2+p.
(4)x2=-2py(p>0)中,|AB|=-y1-y2+p.
基础训练
基础训练1、2、3
基础训练
基础训练4、5、6
4
(0,-1)
典型例题
典型例题1
【例1】
已知椭圆的中心在原点,焦点在坐标轴上,又过点
P(3,2),长轴长是短轴长的3倍,求该椭圆的方程。
解:由题知,椭圆的方程为标准方程。
小结:本题用待定系数法求椭圆的标准方程,
但在无法判断焦点所在的坐标轴时,要分情况讨论
历年真题
历年真题
历年真题
历年真题
课堂小结
本节课主要复习圆锥曲线的定义、标准方程、
几何性质及应用,同时注重与其他知识的综合
运用,在解题时除了要熟练掌握圆锥曲线基本知
识外,需注重利用数形结合思想解决实际问题。
课堂小结
