人教版 九年级数学(下) 26.1 反比例函数 同步练习卷 (含解析)
文档属性
| 名称 | 人教版 九年级数学(下) 26.1 反比例函数 同步练习卷 (含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-12 00:00:00 | ||
图片预览




文档简介
第26章 第一节 反比例函数 同步练习卷
一、选择题
1.已知是反比例函数,则函数图象在
A.第一,三象限 B.第二,四象限 C.第一,二象限 D.第三,四象限
2.在反比例函数的图象的每个象限内,随的增大而增大,则值可以是
A. B.1 C.2 D.3
3.已知反比例函数的图象经过点,,则的值为
A.0.5 B.1 C.2 D.4
4.下列函数中,随着的增大而减小的是
A. B. C. D.
5.直线与函数的图象有且只有一个公共点,则的值为
A.2 B. C. D.
6.若点,,,,,在反比例函数的图象上,且,则下列各式正确的是
A. B. C. D.
7.如图,过反比例函数图象上的一点作轴于点,连接,若,则的值是
A.2 B. C.4 D.
8.如图,正方形的边长是2,反比例函数图象经过点,则的值是
A.2 B. C.4 D.
9.如图,、是曲线上的点,经过、两点向轴、轴作垂线段,若,则
A.4 B.5 C.6 D.8
10.如图,双曲线与直线交于点,,并且点坐标为,点坐标为,根据图象信息可得关于的不等式的解为
A. B. C. D.或
二.填空题(共10小题)
11.若点在反比例函数的图象上,则 .
12.已知点、在函数的图象上,那么 (填“”或“”或“”
13.已知反比例函数的图象有一分支在第二象限,那么常数的取值范围是 .
14.直线与函数的图象交于点,若,则的取值范围是 .
15.已知反比例函数的图象上有两点,,,,且,,那么与之间的大小关系是 .
16.若直线与双曲线相交于点、,若点的坐标为,则点的坐标为 .
17.如图,一次函数和反比例函数的图象相交于,两点,则使成立的取值范围是 .
18.如图,已知两个反比例函数和在第一象限内的图象,设点在上,轴于点,交于点,轴于点,交于点,则四边形的面积为 .
19.如图,点在双曲线上,点在双曲线上,且轴,过点、分别向轴作垂线,垂足分别为点、,那么四边形的面积是 .
20.如图,正方形的边长为10,点的坐标为,点在轴上.若反比例函数的图象经过点,则的值为 .
三.解答题(共8小题)
21.已知,其中与成正比例,与成反比例,并且当时,当时,求与之间的函数关系式.
22.已知与成反比例,且当时,.
(1)求与的函数关系式;
(2)当时,求的值.
23.反比例函数与一次函数的图象都过.
(1)求点坐标;
(2)求反比例函数解析式.
24.如图,已知一次函数的图象与反比例函数的图象交于,两点.
(1)请直接写出不等式的解集;
(2)求反比例函数和一次函数的解析式;
(3)过点作轴的垂线,垂足为,连接,求的面积.
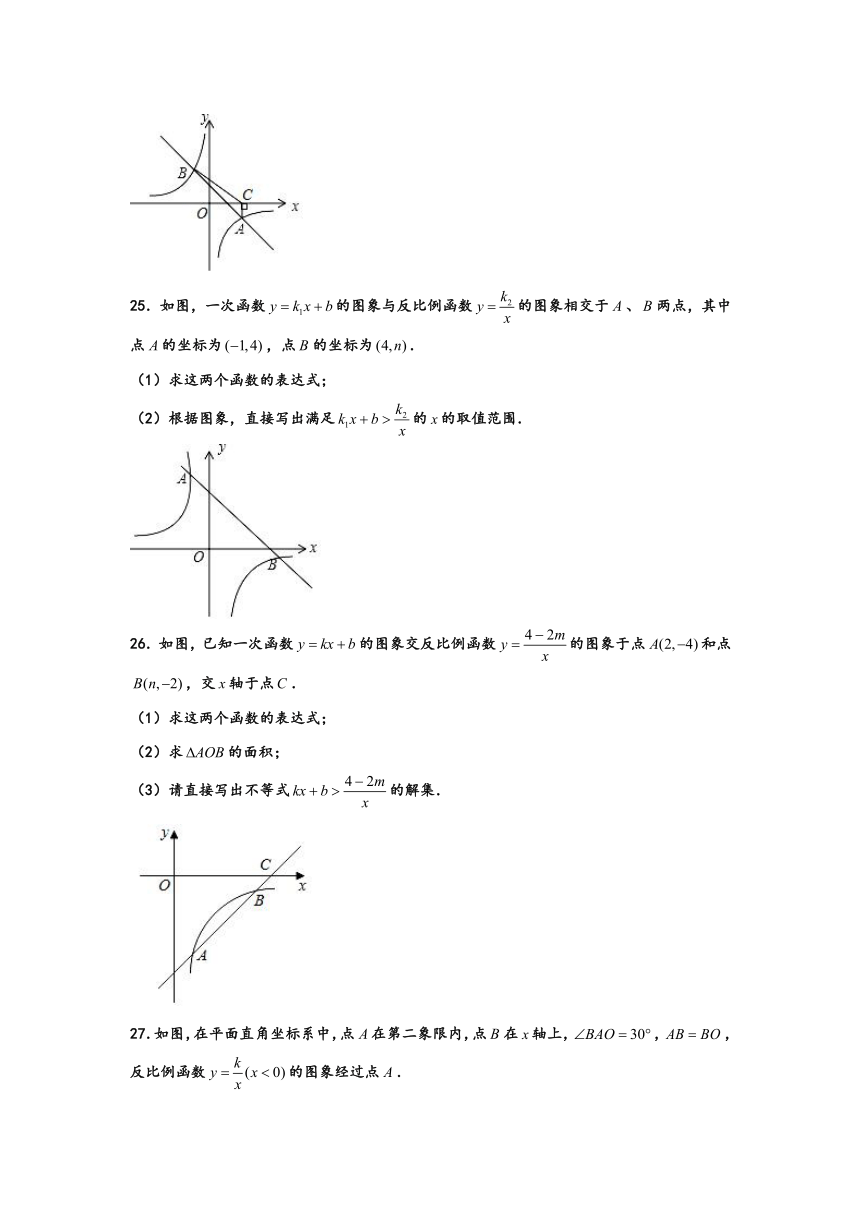
25.如图,一次函数的图象与反比例函数的图象相交于、两点,其中点的坐标为,点的坐标为.
(1)求这两个函数的表达式;
(2)根据图象,直接写出满足的的取值范围.
26.如图,已知一次函数的图象交反比例函数的图象于点和点,交轴于点.
(1)求这两个函数的表达式;
(2)求的面积;
(3)请直接写出不等式的解集.
27.如图,在平面直角坐标系中,点在第二象限内,点在轴上,,,反比例函数的图象经过点.
(1)求的度数;
(2)若,求点的坐标;
(3)若,求反比例函数的解析式.
28.已知,如图所示的双曲线是函数为常数,图象的一支.
(1)求常数的取值范围;
(2)若该函数的图象与一次函数的图象在第一象限的交点为,求点的坐标及反比例函数的表达式.
参考答案
一.选择题(共10小题)
1.已知是反比例函数,则函数图象在
A.第一,三象限 B.第二,四象限 C.第一,二象限 D.第三,四象限
解:依题意有,
解得,
因而函数是,
故函数经过第一,三象限.
故选:.
2.在反比例函数的图象的每个象限内,随的增大而增大,则值可以是
A. B.1 C.2 D.3
解:因为的图象,在每个象限内,的值随值的增大而增大,
所以,
即.
故选:.
3.已知反比例函数的图象经过点,,则的值为
A.0.5 B.1 C.2 D.4
解:将点代入解析式得,
,
.
故选:.
4.下列函数中,随着的增大而减小的是
A. B. C. D.
解:、中,随着的增大而增大,不符合题意;
、中,在每个象限内随着的增大而减小,不符合题意;
、中,随着的增大而减小,符合题意;
、中,在每个象限内随着的增大而增大,不符合题意;
故选:.
5.直线与函数的图象有且只有一个公共点,则的值为
A.2 B. C. D.
解:解得,
线与函数的图象有且只有一个公共点,
△,
,
故选:.
6.若点,,,,,在反比例函数的图象上,且,则下列各式正确的是
A. B. C. D.
解:反比例函数为,
函数图象在第二、四象限,在每个象限内,随着的增大而增大,
又,
,,
,
故选:.
7.如图,过反比例函数图象上的一点作轴于点,连接,若,则的值是
A.2 B. C.4 D.
解:,
,
,
由图可知,反比例函数图象位于第二四象限,
所以,,
.
故选:.
8.如图,正方形的边长是2,反比例函数图象经过点,则的值是
A.2 B. C.4 D.
解:正方形的边长是2,
,
在第三象限,
,
把代入反比例解析式得:,
故选:.
9.如图,、是曲线上的点,经过、两点向轴、轴作垂线段,若,则
A.4 B.5 C.6 D.8
解:、是曲线上的点,经过、两点向轴、轴作垂线段,
,
又,
,
.
故选:.
10.如图,双曲线与直线交于点,,并且点坐标为,点坐标为,根据图象信息可得关于的不等式的解为
A. B. C. D.或
解:点坐标为,点坐标为,
关于不等式的解集为:或,
故选:.
二.填空题(共10小题)
11.若点在反比例函数的图象上,则 .
解:将点代入反比例函数得,
.
故答案为.
12.已知点、在函数的图象上,那么 (填“”或“”或“”
解:把点、分别代入函数中得,,,
,
,
故答案为:.
13.已知反比例函数的图象有一分支在第二象限,那么常数的取值范围是 .
解:反比例函数的图象有一分支在第二象限,
,
解得,
故答案是:.
14.直线与函数的图象交于点,若,则的取值范围是 或 .
解:直线与函数的图象交于点,
直线与函数的图象交于另一个点的坐标是,
如图,若,则的取值范围是或,
故答案为或.
15.已知反比例函数的图象上有两点,,,,且,,那么与之间的大小关系是 .
解:反比例函数中,
此函数图象在一、三象限,
,,
,在第三象限;点,在第一象限,
,,
.
故答案为:.
16.若直线与双曲线相交于点、,若点的坐标为,则点的坐标为 .
解:把点的坐标代入直线与双曲线的解析式得:,,
解得:,,
即,,
解方程组得:,,
点的坐标为,
点的坐标为,
故答案为:.
17.如图,一次函数和反比例函数的图象相交于,两点,则使成立的取值范围是 或 .
解:观察函数图象可发现:当或时,一次函数图象在反比例函数图象上方,
使成立的取值范围是或.
故答案为:或.
18.如图,已知两个反比例函数和在第一象限内的图象,设点在上,轴于点,交于点,轴于点,交于点,则四边形的面积为 .
解:轴,轴,
,,
四边形的面积,
故答案为.
19.如图,点在双曲线上,点在双曲线上,且轴,过点、分别向轴作垂线,垂足分别为点、,那么四边形的面积是 2 .
解:过点作轴于点,
点在双曲线上,点在双曲线上,
矩形的面积为:1,矩形的面积是3,
矩形的面积为:,
故答案为2.
20.如图,正方形的边长为10,点的坐标为,点在轴上.若反比例函数的图象经过点,则的值为 12 .
解:如图,过点作轴于,在正方形中,,,
,
,
,
点的坐标为,
,
,
,
在和中,
,
,
,,
,
点的坐标为,
反比例函数的图象过点,
,
故答案为12.
三.解答题(共8小题)
21.已知,其中与成正比例,与成反比例,并且当时,当时,求与之间的函数关系式.
解:与成正比例,与成反比例,
,,
,
,
当时,当时,
,
解得:,
与之间的函数关系式为.
22.已知与成反比例,且当时,.
(1)求与的函数关系式;
(2)当时,求的值.
解:依题意可设,则,
.
该函数解析式为.
(2)当时,.
即当时,函数的值是.
23.反比例函数与一次函数的图象都过.
(1)求点坐标;
(2)求反比例函数解析式.
解:(1)将点代入得:
,
解得:,
点的坐标为;
(2)将点代入得:,
反比例函数解析式为.
24.如图,已知一次函数的图象与反比例函数的图象交于,两点.
(1)请直接写出不等式的解集;
(2)求反比例函数和一次函数的解析式;
(3)过点作轴的垂线,垂足为,连接,求的面积.
解:(1)由图象可知:不等式的解集为或;
(2)一次函数的图象与反比例函数的图象交于,两点.
,
解得,,,
反比例函数和一次函数的解析式分别为,;
(3).
25.如图,一次函数的图象与反比例函数的图象相交于、两点,其中点的坐标为,点的坐标为.
(1)求这两个函数的表达式;
(2)根据图象,直接写出满足的的取值范围.
解:(1)把点代入反比例函数得,,
反比例函数的解析式为,
将点代入得,,
,
将、的坐标代入得,
解得,
一次函数的解析式为;
(2)由图象可知:当或时,.
26.如图,已知一次函数的图象交反比例函数的图象于点和点,交轴于点.
(1)求这两个函数的表达式;
(2)求的面积;
(3)请直接写出不等式的解集.
解:(1)把的坐标代入得:,
反比例函数的表达式是;
把的坐标代入得:,
解得:,
点坐标为,
把、的坐标代入并解得:
,,
一次函数表达式为;
(2)当时,,
,
的面积;
(3)由图象知,或.
27.如图,在平面直角坐标系中,点在第二象限内,点在轴上,,,反比例函数的图象经过点.
(1)求的度数;
(2)若,求点的坐标;
(3)若,求反比例函数的解析式.
【解答】解(1),
;
(2)过点作轴于,
,
,,
;
(3)设,
,
,
在直角三角形中得出,
,
,
,
,
,
,
,
把点坐标代入得,,
解得
反比例函数的解析式为.
28.已知,如图所示的双曲线是函数为常数,图象的一支.
(1)求常数的取值范围;
(2)若该函数的图象与一次函数的图象在第一象限的交点为,求点的坐标及反比例函数的表达式.
解:(1)根据图象得,解得;
(2)点在一次函数的图象上,
,则点的坐标为.
又点在反比例函数为常数,的图象上,
,
反比例函数的表达式为.
