辽宁省鞍山市台安县2020年高一年级下学期必修三册7.3.1节正弦函数的性质与图像(共16张PPT)
文档属性
| 名称 | 辽宁省鞍山市台安县2020年高一年级下学期必修三册7.3.1节正弦函数的性质与图像(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-13 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
*
*
杨奎 02 10班
*
*
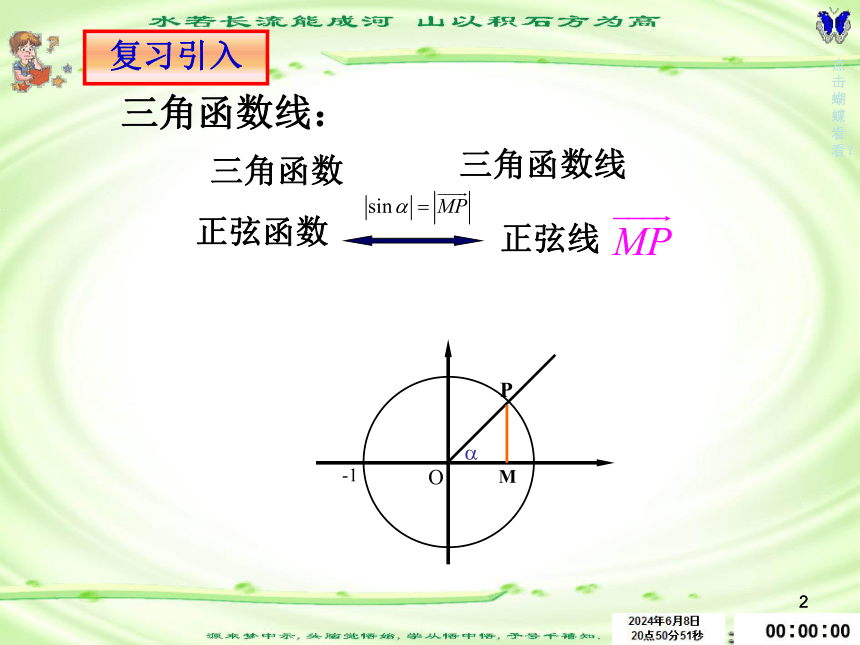
三角函数
三角函数线
正弦函数
?
P
M
三角函数线:
复习引入
*
*
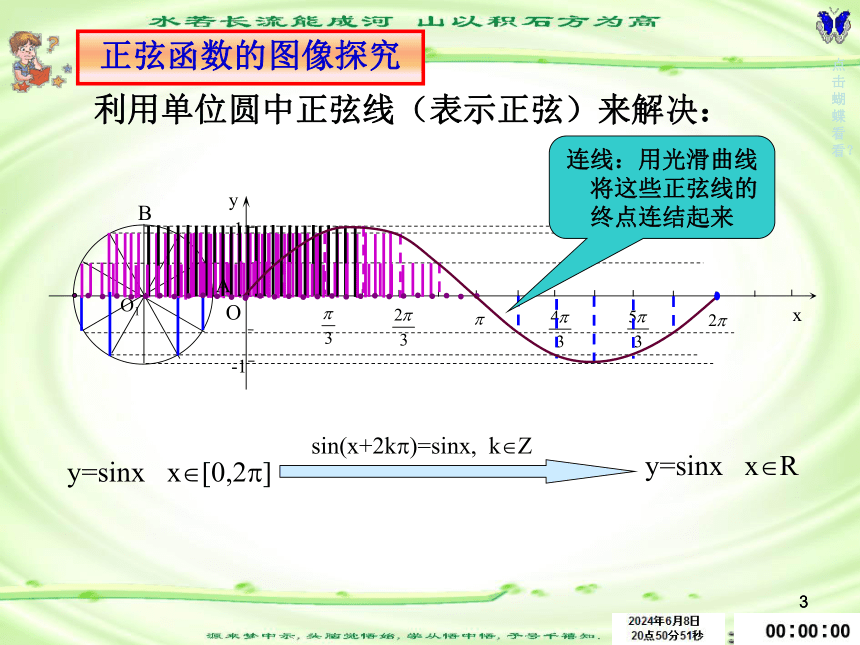
利用单位圆中正弦线(表示正弦)来解决:
y=sinx x?[0,2?]
y=sinx x?R
sin(x+2k?)=sinx, k?Z
连线:用光滑曲线
将这些正弦线的终点连结起来
A
B
正弦函数的图像探究
*
正弦曲线
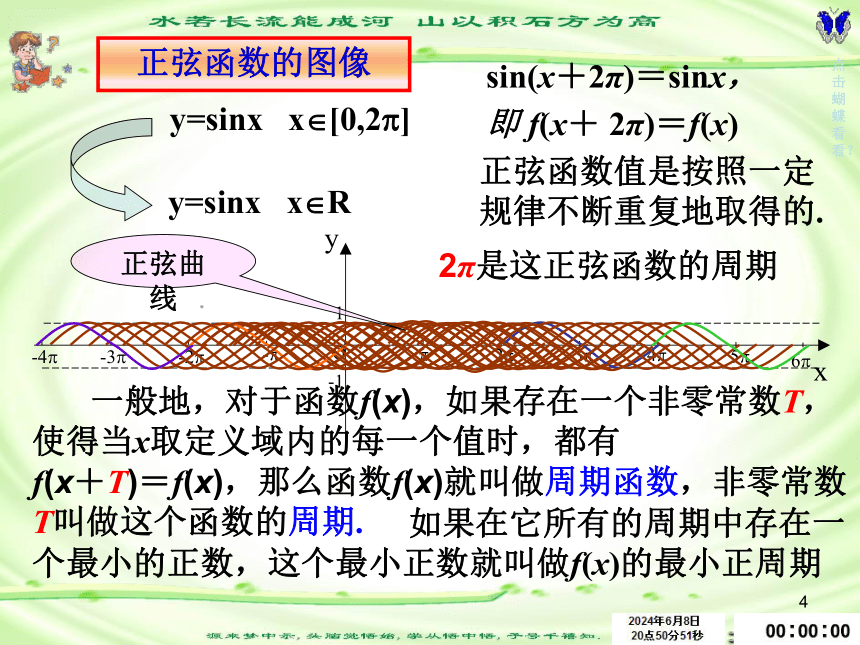
正弦函数的图像
sin(x+2π)=sinx,
即 f(x+ 2π)=f(x)
正弦函数值是按照一定规律不断重复地取得的.
2π是这正弦函数的周期
一般地,对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有
f(x+T)=f(x),那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期.
如果在它所有的周期中存在一个最小的正数,这个最小正数就叫做f(x)的最小正周期
*
观察正弦函数的图像填表
递增区间是
递减区间是
对称中心是
对称轴是
,
,
定义域:
值域:
奇偶性:
最值:
周期性:
*
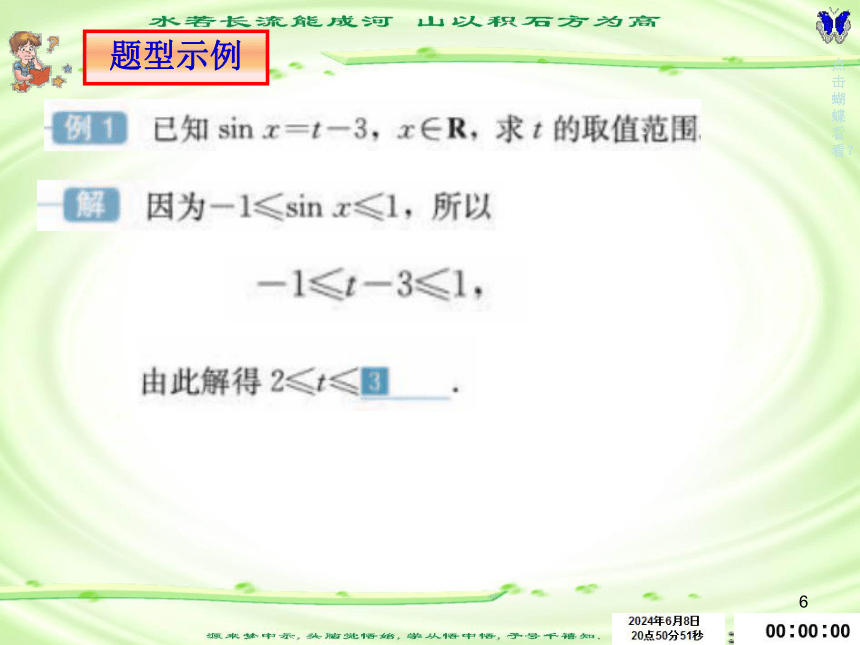
题型示例
*
题型示例
例2. 不求值,
解:∵
是增函数
*
*
*
*
如何作出正弦函数的图象(在精确度要求不太高时)?
(0,0)
( ? ,0)
( 2? ,0)
五点法——
0
1
0
-1
0
五个关键点-五点法作简图
x
sinx
*
*
例4 画出函数y=1+sinx,x?[0, 2?]的简图:
0
1
0
-1
0
1 2 1 0 1
y=sinx,x?[0, 2?]
y=1+sinx,x?[0, 2?]
“五点法”作图示例
x
sinx
1+sinx
*
题型示例
训1 求下列三角函数的周期:
解:
因为sin(2?+z)=sinz
即 f (x+2?)=f (x)
∴周期T=2?
则3sin(z+2?)=3sinz
即 f (x+4?)=f (x)
∴周期T=4?
*
求周期的一般公式
(1)y=sin2x(x∈R)的周期为2π/2=π;
的周期为2π/(1/2)=4π.
*
训2 函数 在什么区间上是增函数?
题型示例
解:要使函数
为增函数
,当且仅当
(k∈Z)
∴ 函数 在区间
上是增函数
*
定义域:
递增区间是
递减区间是
对称中心是
对称轴是
,
,
值域:
奇偶性:
最值:
周期性:
课堂小结
y=sinx的性质
*
再见!
知识是宝库,而实践是开启宝库的钥匙.
作业:大本19-21;小本73-74
*
*
杨奎 02 10班
*
*
三角函数
三角函数线
正弦函数
?
P
M
三角函数线:
复习引入
*
*
利用单位圆中正弦线(表示正弦)来解决:
y=sinx x?[0,2?]
y=sinx x?R
sin(x+2k?)=sinx, k?Z
连线:用光滑曲线
将这些正弦线的终点连结起来
A
B
正弦函数的图像探究
*
正弦曲线
正弦函数的图像
sin(x+2π)=sinx,
即 f(x+ 2π)=f(x)
正弦函数值是按照一定规律不断重复地取得的.
2π是这正弦函数的周期
一般地,对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有
f(x+T)=f(x),那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期.
如果在它所有的周期中存在一个最小的正数,这个最小正数就叫做f(x)的最小正周期
*
观察正弦函数的图像填表
递增区间是
递减区间是
对称中心是
对称轴是
,
,
定义域:
值域:
奇偶性:
最值:
周期性:
*
题型示例
*
题型示例
例2. 不求值,
解:∵
是增函数
*
*
*
*
如何作出正弦函数的图象(在精确度要求不太高时)?
(0,0)
( ? ,0)
( 2? ,0)
五点法——
0
1
0
-1
0
五个关键点-五点法作简图
x
sinx
*
*
例4 画出函数y=1+sinx,x?[0, 2?]的简图:
0
1
0
-1
0
1 2 1 0 1
y=sinx,x?[0, 2?]
y=1+sinx,x?[0, 2?]
“五点法”作图示例
x
sinx
1+sinx
*
题型示例
训1 求下列三角函数的周期:
解:
因为sin(2?+z)=sinz
即 f (x+2?)=f (x)
∴周期T=2?
则3sin(z+2?)=3sinz
即 f (x+4?)=f (x)
∴周期T=4?
*
求周期的一般公式
(1)y=sin2x(x∈R)的周期为2π/2=π;
的周期为2π/(1/2)=4π.
*
训2 函数 在什么区间上是增函数?
题型示例
解:要使函数
为增函数
,当且仅当
(k∈Z)
∴ 函数 在区间
上是增函数
*
定义域:
递增区间是
递减区间是
对称中心是
对称轴是
,
,
值域:
奇偶性:
最值:
周期性:
课堂小结
y=sinx的性质
*
再见!
知识是宝库,而实践是开启宝库的钥匙.
作业:大本19-21;小本73-74
