第三章 图形的平移与旋转综合能力测试卷(含解析)
文档属性
| 名称 | 第三章 图形的平移与旋转综合能力测试卷(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-13 00:00:00 | ||
图片预览



文档简介
第三章 综合能力测试卷
时间120分钟 满分120分
一.选择题(每小题3分,共36分)
1.(2019?鸡西)下列图形是我国国产品牌汽车的标识,其中是中心对称图形的是( )
A. B.
C. D.
2.(2019春?西湖区校级期中)下列现象中,不属于平移的是( )
A.滑雪运动员在平坦的雪地上滑行
B.钟摆的摆动
C.大楼上上下下迎送来客的电梯
D.火车在笔直的铁轨上飞驰而过
3.(2019秋?汝阳县期中)如图是6级台阶侧面示意图,如果要在台阶上铺红地毯,那么地毯长度至少需要( )
A.8米 B.5米 C.4米 D.3米
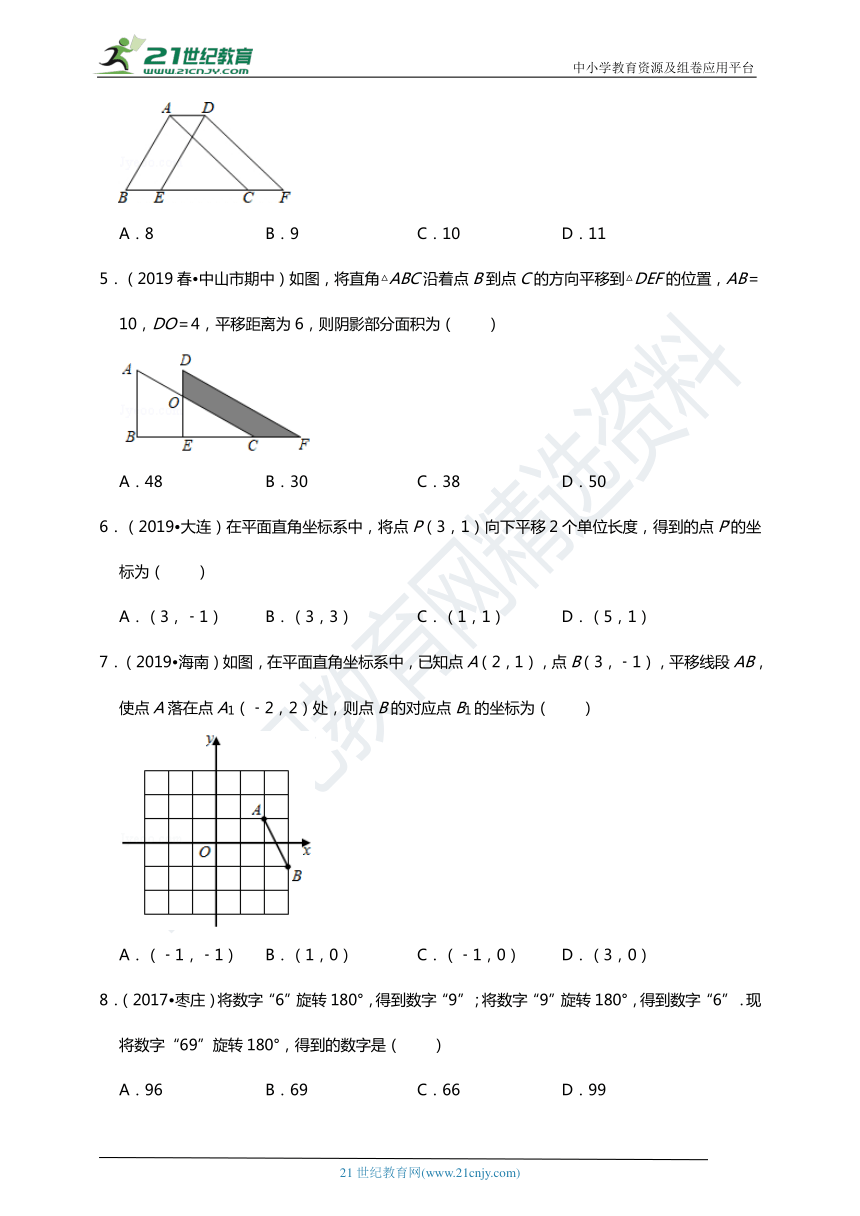
4.(2019春?鹿城区校级期中)如图,将△ABC沿BC方向向右平移3个单位得到△DEF,已知四边形ABFD的周长为16.求△ABC的周长( )
A.8 B.9 C.10 D.11
5.(2019春?中山市期中)如图,将直角△ABC沿着点B到点C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A.48 B.30 C.38 D.50
6.(2019?大连)在平面直角坐标系中,将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为( )
A.(3,﹣1) B.(3,3) C.(1,1) D.(5,1)
7.(2019?海南)如图,在平面直角坐标系中,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在点A1(﹣2,2)处,则点B的对应点B1的坐标为( )
A.(﹣1,﹣1) B.(1,0) C.(﹣1,0) D.(3,0)
8.(2017?枣庄)将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
9.(2019?湘潭)如图,将△OAB绕点O逆时针旋转70°到△OCD的位置,若∠AOB=40°,则∠AOD=( )
A.45° B.40° C.35° D.30°
10.(2019?天津)如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是( )
A.AC=AD B.AB⊥EB C.BC=DE D.∠A=∠EBC
11.(2019?吉林)把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A.30° B.90° C.120° D.180°
12.(2018?潍坊)在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
A.Q(3,240°) B.Q(3,﹣120°) C.Q(3,600°) D.Q(3,﹣500°)
二.填空题(每小题4分,共24分)
13.(2019?曲靖二模)如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE=
14.(2019?郫都区模拟)如图,在长方形ABCD中,AB=7cm,BC=10cm,现将长方形ABCD向右平移3cm,再向下平移4cm后到长方形A'B'C'D'的位置,A'B'交BC于点E,A'D'交DC于点F,那么长方形A'ECF的周长为 cm.
15.(2020?百色模拟)三角形ABC中任意一点P(x0,y0)经平移后対应点为P1(x0+5,y0+3),将三角形ABC作同样的平移得到三角形A1B1C1,若A(﹣2,3),则A1的坐标为 .
16.(2019秋?天河区校级期中)如图,△ABC绕着点C旋转至△DEC,点B,C,D共线,∠B=90°,∠A=30°,BC=1,则BD= .
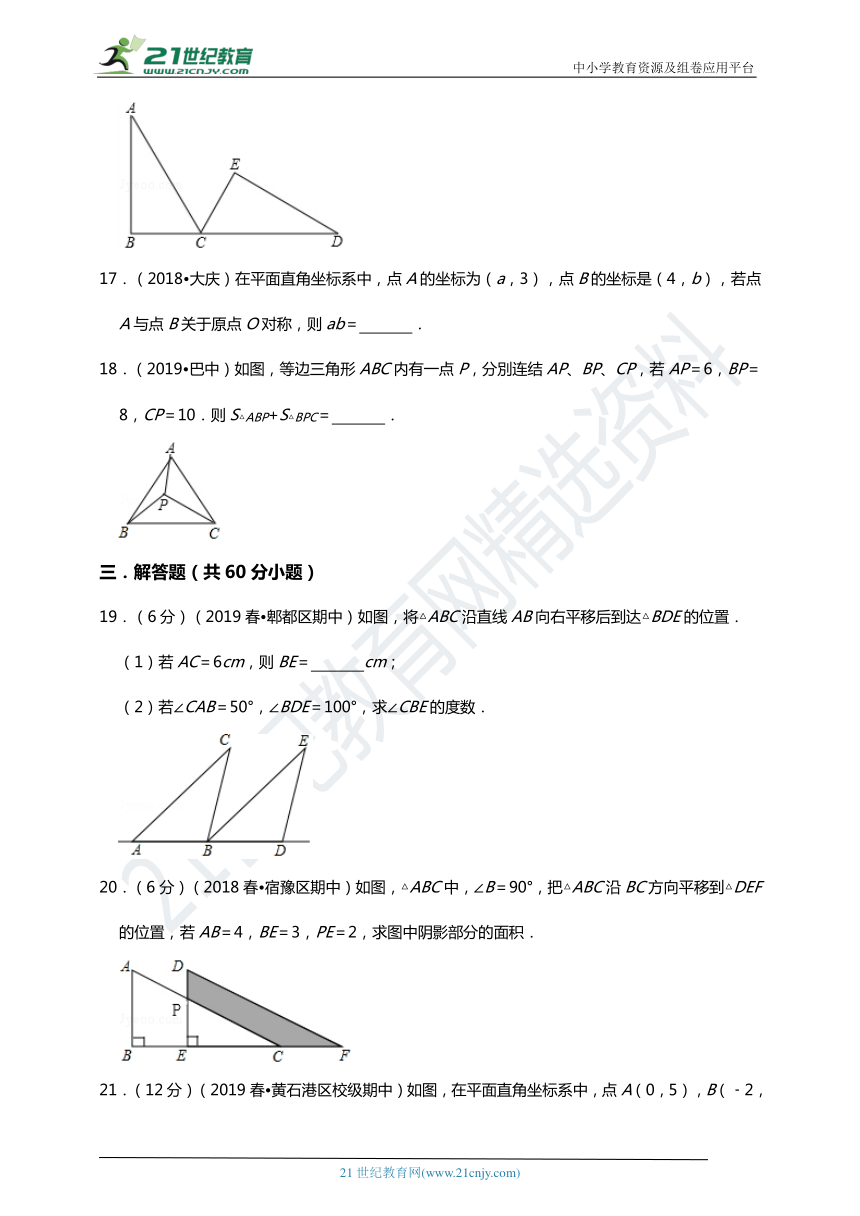
17.(2018?大庆)在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点O对称,则ab= .
18.(2019?巴中)如图,等边三角形ABC内有一点P,分別连结AP、BP、CP,若AP=6,BP=8,CP=10.则S△ABP+S△BPC= .
三.解答题(共60分小题)
19.(6分)(2019春?郫都区期中)如图,将△ABC沿直线AB向右平移后到达△BDE的位置.
(1)若AC=6cm,则BE= cm;
(2)若∠CAB=50°,∠BDE=100°,求∠CBE的度数.
20.(6分)(2018春?宿豫区期中)如图,△ABC中,∠B=90°,把△ABC沿BC方向平移到△DEF的位置,若AB=4,BE=3,PE=2,求图中阴影部分的面积.
21.(12分)(2019春?黄石港区校级期中)如图,在平面直角坐标系中,点A(0,5),B(﹣2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点C,点D在第一象限,直线AC交x轴于点F.
(1)点D坐标为 ;
(2)线段CD由线段AB经过怎样平移得到?
(3)求△BCF的面积.
22.(8分)(2019?苏州)如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
23.(8分)(2016?荆门)如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
24.(10分)(2013?福州)如图,在平面直角坐标系xOy中,点A的坐标为(﹣2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个单位长度;△AOC与△BOD关于直线对称,则对称轴是 ;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是 度;
(2)连结AD,交OC于点E,求∠AEO的度数.
25.(10分)(2011?聊城)将两块大小相同的含30°角的直角三角板(∠BAC=∠B′A′C=30°)按图①方式放置,固定三角板A′B′C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A′C交于点E,AC与A′B′交于点F,AB与A′B′相交于点O.
(1)求证:△BCE≌△B′CF;
(2)当旋转角等于30°时,AB与A′B′垂直吗?请说明理由.
第三章综合能力测试卷
参考答案与试题解析
一.选择题
1.(2019?鸡西)下列图形是我国国产品牌汽车的标识,其中是中心对称图形的是( )
A. B.
C. D.
【分析】根据中心对称图形的概念求解即可.
【解答】解:A、不是中心对称图形,本选项错误;
B、不是中心对称图形,本选项错误;
C、是中心对称图形,本选项正确;
D、不是中心对称图形,本选项错误.
故选:C.
2.(2019春?西湖区校级期中)下列现象中,不属于平移的是( )
A.滑雪运动员在平坦的雪地上滑行
B.钟摆的摆动
C.大楼上上下下迎送来客的电梯
D.火车在笔直的铁轨上飞驰而过
【分析】根据平移不改变图形的形状、大小和方向,结合图形对选项进行一一分析,选出正确答案.
【解答】解:A、滑雪运动员在平坦的雪地上滑雪,属于平移得到,故本选项不合题意;
B、钟摆的摆动,不属于平移得到,故本选项符合题意;
C、大楼上上下下迎送来客的电梯,属于平移得到,故本选项不合题意;
D、火车在笔直的铁轨上飞驰而过,属于平移得到,故本选项不合题意.
故选:B.
3.(2019秋?汝阳县期中)如图是6级台阶侧面示意图,如果要在台阶上铺红地毯,那么地毯长度至少需要( )
A.8米 B.5米 C.4米 D.3米
【分析】根据六级台阶的高等于3米,六级台阶的长等于5米求解即可.
【解答】解:∵六级台阶的高等于3米,六级台阶的长等于5米,
∴要买地毯的长:3+5=8(米).
故选:A.
4.(2019春?鹿城区校级期中)如图,将△ABC沿BC方向向右平移3个单位得到△DEF,已知四边形ABFD的周长为16.求△ABC的周长( )
A.8 B.9 C.10 D.11
【分析】先根据平移的性质得出AD=3,BF=BC+CF=BC+3,DF=AC,再根据四边形ABFD的周长=16即可得出结论.
【解答】解:∵将△ABC沿边BC向右平移13个单位得到△DEF,
∴AD=3,BF=BC+CF=BC+3,DF=AC,
又∵AB+BF+DF+AD=16,
∴△ABC的周长=AB+BC+AC=16﹣3﹣3=10.
故选:C.
5.(2019春?中山市期中)如图,将直角△ABC沿着点B到点C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A.48 B.30 C.38 D.50
【分析】先利用平移的性质得到S△ABC=S△DEF,DE=AB=10,BE=6,则OE=4,再利用面积的和差得到阴影部分面积=S梯形ABEO,然后根据梯形的面积公式计算即可.
【解答】解:∵直角△ABC沿着点B到点C的方向平移到△DEF的位置,
∴S△ABC=S△DEF,DE=AB=10,BE=6,
∴OE=DE﹣DO=10﹣4=6,
∵阴影部分面积=S△DEF﹣S△OEC=S△ABC﹣S△OEC=S梯形ABEO=×(6+10)×6=48.
故选:A.
6.(2019?大连)在平面直角坐标系中,将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为( )
A.(3,﹣1) B.(3,3) C.(1,1) D.(5,1)
【分析】根据向下平移,横坐标不变、纵坐标相减列式计算即可得解.
【解答】解:将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为(3,1﹣2),即(3,﹣1),
故选:A.
7.(2019?海南)如图,在平面直角坐标系中,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在点A1(﹣2,2)处,则点B的对应点B1的坐标为( )
A.(﹣1,﹣1) B.(1,0) C.(﹣1,0) D.(3,0)
【分析】由点A(2,1)平移后A1(﹣2,2)可得坐标的变化规律,由此可得点B的对应点B1的坐标.
【解答】解:由点A(2,1)平移后A1(﹣2,2)可得坐标的变化规律是:左移4个单位,上移1个单位,
∴点B的对应点B1的坐标(﹣1,0).
故选:C.
8.(2017?枣庄)将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
【分析】直接利用中心对称图形的性质结合69的特点得出答案.
【解答】解:现将数字“69”旋转180°,得到的数字是:69.
故选:B.
9.(2019?湘潭)如图,将△OAB绕点O逆时针旋转70°到△OCD的位置,若∠AOB=40°,则∠AOD=( )
A.45° B.40° C.35° D.30°
【分析】首先根据旋转角定义可以知道∠BOD=70°,而∠AOB=40°,然后根据图形即可求出∠AOD.
【解答】解:∵△OAB绕点O逆时针旋转70°到△OCD的位置,
∴∠BOD=70°,
而∠AOB=40°,
∴∠AOD=70°﹣40°=30°.
故选:D.
10.(2019?天津)如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是( )
A.AC=AD B.AB⊥EB C.BC=DE D.∠A=∠EBC
【分析】根据旋转的性质得到AC=CD,BC=CE,AB=DE,故A错误,C错误;
得到∠ACD=∠BCE,根据三角形的内角和得到∠A=∠ADC=,∠CBE=,求得∠A=∠EBC,故D正确;由于∠A+∠ABC不一定等于90°,于是得到∠ABC+∠CBE不一定等于90°,故B错误.
【解答】解:∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD,BC=CE,AB=DE,故A错误,C错误;
∴∠ACD=∠BCE,
∴∠A=∠ADC=,∠CBE=,
∴∠A=∠EBC,故D正确;
∵∠A+∠ABC不一定等于90°,
∴∠ABC+∠CBE不一定等于90°,故B错误
故选:D.
11.(2019?吉林)把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A.30° B.90° C.120° D.180°
【分析】根据图形的对称性,用360°除以3计算即可得解.
【解答】解:∵360°÷3=120°,
∴旋转的角度是120°的整数倍,
∴旋转的角度至少是120°.
故选:C.
12.(2018?潍坊)在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
A.Q(3,240°) B.Q(3,﹣120°) C.Q(3,600°) D.Q(3,﹣500°)
【分析】根据中心对称的性质解答即可.
【解答】解:∵P(3,60°)或P(3,﹣300°)或P(3,420°),
由点P关于点O成中心对称的点Q可得:点Q的极坐标为(3,240°),(3,﹣120°),(3,600°),
故选:D.
二.填空题
13.(2019?曲靖二模)如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE= 105°
【分析】本题利用平移的性质可求解.
【解答】解:由平移可知∠DEF=∠ABC=75°,
∵BE∥CF,
∴∠EFC=180°﹣∠DEF=180°﹣75°=105°.
故答案是:105°.
14.(2019?郫都区模拟)如图,在长方形ABCD中,AB=7cm,BC=10cm,现将长方形ABCD向右平移3cm,再向下平移4cm后到长方形A'B'C'D'的位置,A'B'交BC于点E,A'D'交DC于点F,那么长方形A'ECF的周长为 20 cm.
【分析】根据平移的距离表示出长方形A'ECF的长和宽,即可求出结论.
【解答】解:由题意得到BE=3cm,DF=4cm,
∵AB=DE=7cm,BC=10cm,
∴EC=10cm﹣3cm=7cm,FC=7cm﹣4cm=3cm,
∴长方形A'ECF的周长=2×(7+3)=20(cm),
故答案为20.
15.(2020?百色模拟)三角形ABC中任意一点P(x0,y0)经平移后対应点为P1(x0+5,y0+3),将三角形ABC作同样的平移得到三角形A1B1C1,若A(﹣2,3),则A1的坐标为 (3,6) .
【分析】根据点P平移前后的坐标,可得出坐标平移规律:横坐标加5,纵坐标加3,从而可得到A1的坐标.
【解答】解:∵三角形ABC中任意一点P(x0,y0)经平移后対应点为P1(x0+5,y0+3),
∴坐标平移规律是:横坐标加5,纵坐标加3,
∴将三角形ABC作同样的平移得到三角形A1B1C1,若A(﹣2,3),则A1的坐标为(﹣2+5,3+3),即(3,6).
故答案为(3,6).
16.(2019秋?天河区校级期中)如图,△ABC绕着点C旋转至△DEC,点B,C,D共线,∠B=90°,∠A=30°,BC=1,则BD= 3 .
【分析】由直角三角形的性质求出AC=2BC,根据旋转的性质可求出CD的长,则BD可求出.
【解答】解:∵∠B=90°,∠A=30°,BC=1,
∴AC=2BC=2,
∵△ABC绕着点C旋转至△DEC,
∴CD=AC=2,
∴BD=BC+CD=1+2=3,
故答案为:3.
17.(2018?大庆)在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点O对称,则ab= 12 .
【分析】直接利用关于原点对称点的性质得出a,b的值,进而得出答案.
【解答】解:∵点A的坐标为(a,3),点B的坐标是(4,b),点A与点B关于原点O对称,
∴a=﹣4,b=﹣3,
则ab=12.
故答案为:12.
18.(2019?巴中)如图,等边三角形ABC内有一点P,分別连结AP、BP、CP,若AP=6,BP=8,CP=10.则S△ABP+S△BPC= 24+16 .
【分析】将△BPC绕点B逆时针旋转60°后得△AP'B,根据旋转的性质可得∠PBP′=∠CAB=60°,BP=BP′,可得△BPP′为等边三角形,可得BP′=BP=8=PP',由勾股定理的逆定理可得,△APP′是直角三角形,由三角形的面积公式可求解.
【解答】解:如图,将△BPC绕点B逆时针旋转60°后得△AP'B,连接PP′,
根据旋转的性质可知,
旋转角∠PBP′=∠CAB=60°,BP=BP′,
∴△BPP′为等边三角形,
∴BP′=BP=8=PP';
由旋转的性质可知,AP′=PC=10,
在△BPP′中,PP′=8,AP=6,
由勾股定理的逆定理得,△APP′是直角三角形,
∴S△ABP+S△BPC=S四边形AP'BP=S△BP'B+S△AP'P=BP2+×PP'×AP=24+16
故答案为:24+16
三.解答题
19.(2019春?郫都区期中)如图,将△ABC沿直线AB向右平移后到达△BDE的位置.
(1)若AC=6cm,则BE= 6 cm;
(2)若∠CAB=50°,∠BDE=100°,求∠CBE的度数.
【分析】(1)由平移性质知△ABC≌△BDE,据此可得BE=AC=6cm;
(2)由△ABC≌△BDE得∠DBE=∠CAB=50°、∠BDE=∠ABC=100°,根据∠CBE=180°﹣∠ABC﹣∠DBE可得答案.
【解答】解:(1)∵将△ABC沿直线AB向右平移得到△BDE,
∴△ABC≌△BDE,
∴BE=AC=6cm,
故答案为:6;
(2)由(1)知△ABC≌△BDE,
∴∠DBE=∠CAB=50°、∠BDE=∠ABC=100°,
∴∠CBE=180°﹣∠ABC﹣∠DBE=30°.
20.(2018春?宿豫区期中)如图,△ABC中,∠B=90°,把△ABC沿BC方向平移到△DEF的位置,若AB=4,BE=3,PE=2,求图中阴影部分的面积.
【分析】根据平移的性质得到S△ABC=S△DEF,则利用S阴影部分+S△PEC=S梯形ABEP+S△PEC得到S阴影部分=S梯形ABEP,然后根据梯形的面积公式求解.
【解答】解:∵△ABC沿BC方向平移到△DEF的位置
∴S△ABC=S△DEF,
∴S阴影部分+S△PEC=S梯形ABEP+S△PEC,
∴S阴影部分=S梯形ABEP=×(4+2)×3=9.
21.(2019春?黄石港区校级期中)如图,在平面直角坐标系中,点A(0,5),B(﹣2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点C,点D在第一象限,直线AC交x轴于点F.
(1)点D坐标为 (5,8) ;
(2)线段CD由线段AB经过怎样平移得到?
(3)求△BCF的面积.
【分析】(1)根据点B移动到A的平移规律可得结论.
(2)根据点B移动到A的平移规律可得结论.
(3)求出直线AC的解析式,可得点F的坐标,再利用三角形的面积公式计算即可.
【解答】解:(1)∵点B向右平移2个单位,再向上平移5个单位得到点A,
∴点C(3,3)向右平移2个单位,再向上平移5个单位得到点D(5,8).
故答案为(5,8).
(2)向右平移5个单位,再向上平移3个单位
(3)设直线AC的解析式为y=kx+b,则有,
解得,
∴直线AC的解析式为y=﹣x+5,
∴点F的坐标为(,0),
∴OF=,
∵OB=2,
∴BF=,
∴S△BCF=×BF×?y=××3=.
22.(2019?苏州)如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
【分析】(1)由旋转的性质可得AC=AF,利用SAS证明△ABC≌△AEF,根据全等三角形的对应边相等即可得出EF=BC;
(2)根据等腰三角形的性质以及三角形内角和定理求出∠BAE=180°﹣65°×2=50°,那么∠FAG=50°.由△ABC≌△AEF,得出∠F=∠C=28°,再根据三角形外角的性质即可求出∠FGC=∠FAG+∠F=78°.
【解答】(1)证明:∵∠CAF=∠BAE,
∴∠BAC=∠EAF.
∵将线段AC绕A点旋转到AF的位置,
∴AC=AF.
在△ABC与△AEF中,
,
∴△ABC≌△AEF(SAS),
∴EF=BC;
(2)解:∵AB=AE,∠ABC=65°,
∴∠BAE=180°﹣65°×2=50°,
∴∠FAG=∠BAE=50°.
∵△ABC≌△AEF,
∴∠F=∠C=28°,
∴∠FGC=∠FAG+∠F=50°+28°=78°.
23.(2016?荆门)如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
【分析】(1)根据题意补全图形,如图所示;
(2)由旋转的性质得到∠DCF为直角,由EF与CD平行,得到∠EFC为直角,利用SAS得到三角形BDC与三角形EFC全等,利用全等三角形对应角相等即可得证.
【解答】解:(1)补全图形,如图所示;
(2)由旋转的性质得:∠DCF=90°,
∴∠DCE+∠ECF=90°,
∵∠ACB=90°,
∴∠DCE+∠BCD=90°,
∴∠ECF=∠BCD,
∵EF∥DC,
∴∠EFC+∠DCF=180°,
∴∠EFC=90°,
在△BDC和△EFC中,
,
∴△BDC≌△EFC(SAS),
∴∠BDC=∠EFC=90°.
24.(2013?福州)如图,在平面直角坐标系xOy中,点A的坐标为(﹣2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 2 个单位长度;△AOC与△BOD关于直线对称,则对称轴是 y轴 ;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是 120 度;
(2)连结AD,交OC于点E,求∠AEO的度数.
【分析】(1)由点A的坐标为(﹣2,0),根据平移的性质得到△AOC沿x轴向右平移2个单位得到△OBD,则△AOC与△BOD关于y轴对称;根据等边三角形的性质得∠AOC=∠BOD=60°,则∠AOD=120°,根据旋转的定义得△AOC绕原点O顺时针旋转120°得到△DOB;
(2)根据旋转的性质得到OA=OD,而∠AOC=∠BOD=60°,得到∠DOC=60°,所以OE为等腰△AOD的顶角的平分线,根据等腰三角形的性质得到OE垂直平分AD,则∠AEO=90°.
【解答】解:(1)∵点A的坐标为(﹣2,0),
∴△AOC沿x轴向右平移2个单位得到△OBD;
∴△AOC与△BOD关于y轴对称;
∵△AOC为等边三角形,
∴∠AOC=∠BOD=60°,
∴∠AOD=120°,
∴△AOC绕原点O顺时针旋转120°得到△DOB.
(2)如图,∵等边△AOC绕原点O顺时针旋转120°得到△DOB,
∴OA=OD,
∵∠AOC=∠BOD=60°,
∴∠DOC=60°,
即OE为等腰△AOD的顶角的平分线,
∴OE垂直平分AD,
∴∠AEO=90°.
故答案为2;y轴;120.
25.(2011?聊城)将两块大小相同的含30°角的直角三角板(∠BAC=∠B′A′C=30°)按图①方式放置,固定三角板A′B′C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A′C交于点E,AC与A′B′交于点F,AB与A′B′相交于点O.
(1)求证:△BCE≌△B′CF;
(2)当旋转角等于30°时,AB与A′B′垂直吗?请说明理由.
【分析】(1)根据题意可知∠B=∠B′,BC=B′C,∠BCE=∠B′CF,利用ASA即可证出△BCE≌△B′CF;
(2)由旋转角等于30°得出∠ECF=30°,所以∠FCB′=60°,根据四边形的内角和可知∠BOB′的度数为
360°﹣60°﹣60°﹣150°,最后计算出∠BOB′的度数即可.
【解答】(1)证明:两块大小相同的含30°角的直角三角板,所以∠BCA=∠B′CA′,
∵∠BCA﹣∠A′CA=∠B′CA′﹣∠A′CA,
即∠BCE=∠B′CF
∵,
∴△BCE≌△B′CF(ASA);
(2)解:AB与A′B′垂直,理由如下:
旋转角等于30°,即∠ECF=30°,
所以∠FCB′=60°,
又∠B=∠B′=60°,
根据四边形的内角和可知∠BOB′的度数为360°﹣60°﹣60°﹣150°=90°,
所以AB与A′B′垂直.
时间120分钟 满分120分
一.选择题(每小题3分,共36分)
1.(2019?鸡西)下列图形是我国国产品牌汽车的标识,其中是中心对称图形的是( )
A. B.
C. D.
2.(2019春?西湖区校级期中)下列现象中,不属于平移的是( )
A.滑雪运动员在平坦的雪地上滑行
B.钟摆的摆动
C.大楼上上下下迎送来客的电梯
D.火车在笔直的铁轨上飞驰而过
3.(2019秋?汝阳县期中)如图是6级台阶侧面示意图,如果要在台阶上铺红地毯,那么地毯长度至少需要( )
A.8米 B.5米 C.4米 D.3米
4.(2019春?鹿城区校级期中)如图,将△ABC沿BC方向向右平移3个单位得到△DEF,已知四边形ABFD的周长为16.求△ABC的周长( )
A.8 B.9 C.10 D.11
5.(2019春?中山市期中)如图,将直角△ABC沿着点B到点C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A.48 B.30 C.38 D.50
6.(2019?大连)在平面直角坐标系中,将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为( )
A.(3,﹣1) B.(3,3) C.(1,1) D.(5,1)
7.(2019?海南)如图,在平面直角坐标系中,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在点A1(﹣2,2)处,则点B的对应点B1的坐标为( )
A.(﹣1,﹣1) B.(1,0) C.(﹣1,0) D.(3,0)
8.(2017?枣庄)将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
9.(2019?湘潭)如图,将△OAB绕点O逆时针旋转70°到△OCD的位置,若∠AOB=40°,则∠AOD=( )
A.45° B.40° C.35° D.30°
10.(2019?天津)如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是( )
A.AC=AD B.AB⊥EB C.BC=DE D.∠A=∠EBC
11.(2019?吉林)把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A.30° B.90° C.120° D.180°
12.(2018?潍坊)在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
A.Q(3,240°) B.Q(3,﹣120°) C.Q(3,600°) D.Q(3,﹣500°)
二.填空题(每小题4分,共24分)
13.(2019?曲靖二模)如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE=
14.(2019?郫都区模拟)如图,在长方形ABCD中,AB=7cm,BC=10cm,现将长方形ABCD向右平移3cm,再向下平移4cm后到长方形A'B'C'D'的位置,A'B'交BC于点E,A'D'交DC于点F,那么长方形A'ECF的周长为 cm.
15.(2020?百色模拟)三角形ABC中任意一点P(x0,y0)经平移后対应点为P1(x0+5,y0+3),将三角形ABC作同样的平移得到三角形A1B1C1,若A(﹣2,3),则A1的坐标为 .
16.(2019秋?天河区校级期中)如图,△ABC绕着点C旋转至△DEC,点B,C,D共线,∠B=90°,∠A=30°,BC=1,则BD= .
17.(2018?大庆)在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点O对称,则ab= .
18.(2019?巴中)如图,等边三角形ABC内有一点P,分別连结AP、BP、CP,若AP=6,BP=8,CP=10.则S△ABP+S△BPC= .
三.解答题(共60分小题)
19.(6分)(2019春?郫都区期中)如图,将△ABC沿直线AB向右平移后到达△BDE的位置.
(1)若AC=6cm,则BE= cm;
(2)若∠CAB=50°,∠BDE=100°,求∠CBE的度数.
20.(6分)(2018春?宿豫区期中)如图,△ABC中,∠B=90°,把△ABC沿BC方向平移到△DEF的位置,若AB=4,BE=3,PE=2,求图中阴影部分的面积.
21.(12分)(2019春?黄石港区校级期中)如图,在平面直角坐标系中,点A(0,5),B(﹣2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点C,点D在第一象限,直线AC交x轴于点F.
(1)点D坐标为 ;
(2)线段CD由线段AB经过怎样平移得到?
(3)求△BCF的面积.
22.(8分)(2019?苏州)如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
23.(8分)(2016?荆门)如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
24.(10分)(2013?福州)如图,在平面直角坐标系xOy中,点A的坐标为(﹣2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个单位长度;△AOC与△BOD关于直线对称,则对称轴是 ;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是 度;
(2)连结AD,交OC于点E,求∠AEO的度数.
25.(10分)(2011?聊城)将两块大小相同的含30°角的直角三角板(∠BAC=∠B′A′C=30°)按图①方式放置,固定三角板A′B′C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A′C交于点E,AC与A′B′交于点F,AB与A′B′相交于点O.
(1)求证:△BCE≌△B′CF;
(2)当旋转角等于30°时,AB与A′B′垂直吗?请说明理由.
第三章综合能力测试卷
参考答案与试题解析
一.选择题
1.(2019?鸡西)下列图形是我国国产品牌汽车的标识,其中是中心对称图形的是( )
A. B.
C. D.
【分析】根据中心对称图形的概念求解即可.
【解答】解:A、不是中心对称图形,本选项错误;
B、不是中心对称图形,本选项错误;
C、是中心对称图形,本选项正确;
D、不是中心对称图形,本选项错误.
故选:C.
2.(2019春?西湖区校级期中)下列现象中,不属于平移的是( )
A.滑雪运动员在平坦的雪地上滑行
B.钟摆的摆动
C.大楼上上下下迎送来客的电梯
D.火车在笔直的铁轨上飞驰而过
【分析】根据平移不改变图形的形状、大小和方向,结合图形对选项进行一一分析,选出正确答案.
【解答】解:A、滑雪运动员在平坦的雪地上滑雪,属于平移得到,故本选项不合题意;
B、钟摆的摆动,不属于平移得到,故本选项符合题意;
C、大楼上上下下迎送来客的电梯,属于平移得到,故本选项不合题意;
D、火车在笔直的铁轨上飞驰而过,属于平移得到,故本选项不合题意.
故选:B.
3.(2019秋?汝阳县期中)如图是6级台阶侧面示意图,如果要在台阶上铺红地毯,那么地毯长度至少需要( )
A.8米 B.5米 C.4米 D.3米
【分析】根据六级台阶的高等于3米,六级台阶的长等于5米求解即可.
【解答】解:∵六级台阶的高等于3米,六级台阶的长等于5米,
∴要买地毯的长:3+5=8(米).
故选:A.
4.(2019春?鹿城区校级期中)如图,将△ABC沿BC方向向右平移3个单位得到△DEF,已知四边形ABFD的周长为16.求△ABC的周长( )
A.8 B.9 C.10 D.11
【分析】先根据平移的性质得出AD=3,BF=BC+CF=BC+3,DF=AC,再根据四边形ABFD的周长=16即可得出结论.
【解答】解:∵将△ABC沿边BC向右平移13个单位得到△DEF,
∴AD=3,BF=BC+CF=BC+3,DF=AC,
又∵AB+BF+DF+AD=16,
∴△ABC的周长=AB+BC+AC=16﹣3﹣3=10.
故选:C.
5.(2019春?中山市期中)如图,将直角△ABC沿着点B到点C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A.48 B.30 C.38 D.50
【分析】先利用平移的性质得到S△ABC=S△DEF,DE=AB=10,BE=6,则OE=4,再利用面积的和差得到阴影部分面积=S梯形ABEO,然后根据梯形的面积公式计算即可.
【解答】解:∵直角△ABC沿着点B到点C的方向平移到△DEF的位置,
∴S△ABC=S△DEF,DE=AB=10,BE=6,
∴OE=DE﹣DO=10﹣4=6,
∵阴影部分面积=S△DEF﹣S△OEC=S△ABC﹣S△OEC=S梯形ABEO=×(6+10)×6=48.
故选:A.
6.(2019?大连)在平面直角坐标系中,将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为( )
A.(3,﹣1) B.(3,3) C.(1,1) D.(5,1)
【分析】根据向下平移,横坐标不变、纵坐标相减列式计算即可得解.
【解答】解:将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为(3,1﹣2),即(3,﹣1),
故选:A.
7.(2019?海南)如图,在平面直角坐标系中,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在点A1(﹣2,2)处,则点B的对应点B1的坐标为( )
A.(﹣1,﹣1) B.(1,0) C.(﹣1,0) D.(3,0)
【分析】由点A(2,1)平移后A1(﹣2,2)可得坐标的变化规律,由此可得点B的对应点B1的坐标.
【解答】解:由点A(2,1)平移后A1(﹣2,2)可得坐标的变化规律是:左移4个单位,上移1个单位,
∴点B的对应点B1的坐标(﹣1,0).
故选:C.
8.(2017?枣庄)将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
【分析】直接利用中心对称图形的性质结合69的特点得出答案.
【解答】解:现将数字“69”旋转180°,得到的数字是:69.
故选:B.
9.(2019?湘潭)如图,将△OAB绕点O逆时针旋转70°到△OCD的位置,若∠AOB=40°,则∠AOD=( )
A.45° B.40° C.35° D.30°
【分析】首先根据旋转角定义可以知道∠BOD=70°,而∠AOB=40°,然后根据图形即可求出∠AOD.
【解答】解:∵△OAB绕点O逆时针旋转70°到△OCD的位置,
∴∠BOD=70°,
而∠AOB=40°,
∴∠AOD=70°﹣40°=30°.
故选:D.
10.(2019?天津)如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是( )
A.AC=AD B.AB⊥EB C.BC=DE D.∠A=∠EBC
【分析】根据旋转的性质得到AC=CD,BC=CE,AB=DE,故A错误,C错误;
得到∠ACD=∠BCE,根据三角形的内角和得到∠A=∠ADC=,∠CBE=,求得∠A=∠EBC,故D正确;由于∠A+∠ABC不一定等于90°,于是得到∠ABC+∠CBE不一定等于90°,故B错误.
【解答】解:∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD,BC=CE,AB=DE,故A错误,C错误;
∴∠ACD=∠BCE,
∴∠A=∠ADC=,∠CBE=,
∴∠A=∠EBC,故D正确;
∵∠A+∠ABC不一定等于90°,
∴∠ABC+∠CBE不一定等于90°,故B错误
故选:D.
11.(2019?吉林)把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A.30° B.90° C.120° D.180°
【分析】根据图形的对称性,用360°除以3计算即可得解.
【解答】解:∵360°÷3=120°,
∴旋转的角度是120°的整数倍,
∴旋转的角度至少是120°.
故选:C.
12.(2018?潍坊)在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
A.Q(3,240°) B.Q(3,﹣120°) C.Q(3,600°) D.Q(3,﹣500°)
【分析】根据中心对称的性质解答即可.
【解答】解:∵P(3,60°)或P(3,﹣300°)或P(3,420°),
由点P关于点O成中心对称的点Q可得:点Q的极坐标为(3,240°),(3,﹣120°),(3,600°),
故选:D.
二.填空题
13.(2019?曲靖二模)如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE= 105°
【分析】本题利用平移的性质可求解.
【解答】解:由平移可知∠DEF=∠ABC=75°,
∵BE∥CF,
∴∠EFC=180°﹣∠DEF=180°﹣75°=105°.
故答案是:105°.
14.(2019?郫都区模拟)如图,在长方形ABCD中,AB=7cm,BC=10cm,现将长方形ABCD向右平移3cm,再向下平移4cm后到长方形A'B'C'D'的位置,A'B'交BC于点E,A'D'交DC于点F,那么长方形A'ECF的周长为 20 cm.
【分析】根据平移的距离表示出长方形A'ECF的长和宽,即可求出结论.
【解答】解:由题意得到BE=3cm,DF=4cm,
∵AB=DE=7cm,BC=10cm,
∴EC=10cm﹣3cm=7cm,FC=7cm﹣4cm=3cm,
∴长方形A'ECF的周长=2×(7+3)=20(cm),
故答案为20.
15.(2020?百色模拟)三角形ABC中任意一点P(x0,y0)经平移后対应点为P1(x0+5,y0+3),将三角形ABC作同样的平移得到三角形A1B1C1,若A(﹣2,3),则A1的坐标为 (3,6) .
【分析】根据点P平移前后的坐标,可得出坐标平移规律:横坐标加5,纵坐标加3,从而可得到A1的坐标.
【解答】解:∵三角形ABC中任意一点P(x0,y0)经平移后対应点为P1(x0+5,y0+3),
∴坐标平移规律是:横坐标加5,纵坐标加3,
∴将三角形ABC作同样的平移得到三角形A1B1C1,若A(﹣2,3),则A1的坐标为(﹣2+5,3+3),即(3,6).
故答案为(3,6).
16.(2019秋?天河区校级期中)如图,△ABC绕着点C旋转至△DEC,点B,C,D共线,∠B=90°,∠A=30°,BC=1,则BD= 3 .
【分析】由直角三角形的性质求出AC=2BC,根据旋转的性质可求出CD的长,则BD可求出.
【解答】解:∵∠B=90°,∠A=30°,BC=1,
∴AC=2BC=2,
∵△ABC绕着点C旋转至△DEC,
∴CD=AC=2,
∴BD=BC+CD=1+2=3,
故答案为:3.
17.(2018?大庆)在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点O对称,则ab= 12 .
【分析】直接利用关于原点对称点的性质得出a,b的值,进而得出答案.
【解答】解:∵点A的坐标为(a,3),点B的坐标是(4,b),点A与点B关于原点O对称,
∴a=﹣4,b=﹣3,
则ab=12.
故答案为:12.
18.(2019?巴中)如图,等边三角形ABC内有一点P,分別连结AP、BP、CP,若AP=6,BP=8,CP=10.则S△ABP+S△BPC= 24+16 .
【分析】将△BPC绕点B逆时针旋转60°后得△AP'B,根据旋转的性质可得∠PBP′=∠CAB=60°,BP=BP′,可得△BPP′为等边三角形,可得BP′=BP=8=PP',由勾股定理的逆定理可得,△APP′是直角三角形,由三角形的面积公式可求解.
【解答】解:如图,将△BPC绕点B逆时针旋转60°后得△AP'B,连接PP′,
根据旋转的性质可知,
旋转角∠PBP′=∠CAB=60°,BP=BP′,
∴△BPP′为等边三角形,
∴BP′=BP=8=PP';
由旋转的性质可知,AP′=PC=10,
在△BPP′中,PP′=8,AP=6,
由勾股定理的逆定理得,△APP′是直角三角形,
∴S△ABP+S△BPC=S四边形AP'BP=S△BP'B+S△AP'P=BP2+×PP'×AP=24+16
故答案为:24+16
三.解答题
19.(2019春?郫都区期中)如图,将△ABC沿直线AB向右平移后到达△BDE的位置.
(1)若AC=6cm,则BE= 6 cm;
(2)若∠CAB=50°,∠BDE=100°,求∠CBE的度数.
【分析】(1)由平移性质知△ABC≌△BDE,据此可得BE=AC=6cm;
(2)由△ABC≌△BDE得∠DBE=∠CAB=50°、∠BDE=∠ABC=100°,根据∠CBE=180°﹣∠ABC﹣∠DBE可得答案.
【解答】解:(1)∵将△ABC沿直线AB向右平移得到△BDE,
∴△ABC≌△BDE,
∴BE=AC=6cm,
故答案为:6;
(2)由(1)知△ABC≌△BDE,
∴∠DBE=∠CAB=50°、∠BDE=∠ABC=100°,
∴∠CBE=180°﹣∠ABC﹣∠DBE=30°.
20.(2018春?宿豫区期中)如图,△ABC中,∠B=90°,把△ABC沿BC方向平移到△DEF的位置,若AB=4,BE=3,PE=2,求图中阴影部分的面积.
【分析】根据平移的性质得到S△ABC=S△DEF,则利用S阴影部分+S△PEC=S梯形ABEP+S△PEC得到S阴影部分=S梯形ABEP,然后根据梯形的面积公式求解.
【解答】解:∵△ABC沿BC方向平移到△DEF的位置
∴S△ABC=S△DEF,
∴S阴影部分+S△PEC=S梯形ABEP+S△PEC,
∴S阴影部分=S梯形ABEP=×(4+2)×3=9.
21.(2019春?黄石港区校级期中)如图,在平面直角坐标系中,点A(0,5),B(﹣2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点C,点D在第一象限,直线AC交x轴于点F.
(1)点D坐标为 (5,8) ;
(2)线段CD由线段AB经过怎样平移得到?
(3)求△BCF的面积.
【分析】(1)根据点B移动到A的平移规律可得结论.
(2)根据点B移动到A的平移规律可得结论.
(3)求出直线AC的解析式,可得点F的坐标,再利用三角形的面积公式计算即可.
【解答】解:(1)∵点B向右平移2个单位,再向上平移5个单位得到点A,
∴点C(3,3)向右平移2个单位,再向上平移5个单位得到点D(5,8).
故答案为(5,8).
(2)向右平移5个单位,再向上平移3个单位
(3)设直线AC的解析式为y=kx+b,则有,
解得,
∴直线AC的解析式为y=﹣x+5,
∴点F的坐标为(,0),
∴OF=,
∵OB=2,
∴BF=,
∴S△BCF=×BF×?y=××3=.
22.(2019?苏州)如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
【分析】(1)由旋转的性质可得AC=AF,利用SAS证明△ABC≌△AEF,根据全等三角形的对应边相等即可得出EF=BC;
(2)根据等腰三角形的性质以及三角形内角和定理求出∠BAE=180°﹣65°×2=50°,那么∠FAG=50°.由△ABC≌△AEF,得出∠F=∠C=28°,再根据三角形外角的性质即可求出∠FGC=∠FAG+∠F=78°.
【解答】(1)证明:∵∠CAF=∠BAE,
∴∠BAC=∠EAF.
∵将线段AC绕A点旋转到AF的位置,
∴AC=AF.
在△ABC与△AEF中,
,
∴△ABC≌△AEF(SAS),
∴EF=BC;
(2)解:∵AB=AE,∠ABC=65°,
∴∠BAE=180°﹣65°×2=50°,
∴∠FAG=∠BAE=50°.
∵△ABC≌△AEF,
∴∠F=∠C=28°,
∴∠FGC=∠FAG+∠F=50°+28°=78°.
23.(2016?荆门)如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
【分析】(1)根据题意补全图形,如图所示;
(2)由旋转的性质得到∠DCF为直角,由EF与CD平行,得到∠EFC为直角,利用SAS得到三角形BDC与三角形EFC全等,利用全等三角形对应角相等即可得证.
【解答】解:(1)补全图形,如图所示;
(2)由旋转的性质得:∠DCF=90°,
∴∠DCE+∠ECF=90°,
∵∠ACB=90°,
∴∠DCE+∠BCD=90°,
∴∠ECF=∠BCD,
∵EF∥DC,
∴∠EFC+∠DCF=180°,
∴∠EFC=90°,
在△BDC和△EFC中,
,
∴△BDC≌△EFC(SAS),
∴∠BDC=∠EFC=90°.
24.(2013?福州)如图,在平面直角坐标系xOy中,点A的坐标为(﹣2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 2 个单位长度;△AOC与△BOD关于直线对称,则对称轴是 y轴 ;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是 120 度;
(2)连结AD,交OC于点E,求∠AEO的度数.
【分析】(1)由点A的坐标为(﹣2,0),根据平移的性质得到△AOC沿x轴向右平移2个单位得到△OBD,则△AOC与△BOD关于y轴对称;根据等边三角形的性质得∠AOC=∠BOD=60°,则∠AOD=120°,根据旋转的定义得△AOC绕原点O顺时针旋转120°得到△DOB;
(2)根据旋转的性质得到OA=OD,而∠AOC=∠BOD=60°,得到∠DOC=60°,所以OE为等腰△AOD的顶角的平分线,根据等腰三角形的性质得到OE垂直平分AD,则∠AEO=90°.
【解答】解:(1)∵点A的坐标为(﹣2,0),
∴△AOC沿x轴向右平移2个单位得到△OBD;
∴△AOC与△BOD关于y轴对称;
∵△AOC为等边三角形,
∴∠AOC=∠BOD=60°,
∴∠AOD=120°,
∴△AOC绕原点O顺时针旋转120°得到△DOB.
(2)如图,∵等边△AOC绕原点O顺时针旋转120°得到△DOB,
∴OA=OD,
∵∠AOC=∠BOD=60°,
∴∠DOC=60°,
即OE为等腰△AOD的顶角的平分线,
∴OE垂直平分AD,
∴∠AEO=90°.
故答案为2;y轴;120.
25.(2011?聊城)将两块大小相同的含30°角的直角三角板(∠BAC=∠B′A′C=30°)按图①方式放置,固定三角板A′B′C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A′C交于点E,AC与A′B′交于点F,AB与A′B′相交于点O.
(1)求证:△BCE≌△B′CF;
(2)当旋转角等于30°时,AB与A′B′垂直吗?请说明理由.
【分析】(1)根据题意可知∠B=∠B′,BC=B′C,∠BCE=∠B′CF,利用ASA即可证出△BCE≌△B′CF;
(2)由旋转角等于30°得出∠ECF=30°,所以∠FCB′=60°,根据四边形的内角和可知∠BOB′的度数为
360°﹣60°﹣60°﹣150°,最后计算出∠BOB′的度数即可.
【解答】(1)证明:两块大小相同的含30°角的直角三角板,所以∠BCA=∠B′CA′,
∵∠BCA﹣∠A′CA=∠B′CA′﹣∠A′CA,
即∠BCE=∠B′CF
∵,
∴△BCE≌△B′CF(ASA);
(2)解:AB与A′B′垂直,理由如下:
旋转角等于30°,即∠ECF=30°,
所以∠FCB′=60°,
又∠B=∠B′=60°,
根据四边形的内角和可知∠BOB′的度数为360°﹣60°﹣60°﹣150°=90°,
所以AB与A′B′垂直.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
