2020年人教版八年级数学下册 16.2.2二次根式的除法课件(共16张PPT)
文档属性
| 名称 | 2020年人教版八年级数学下册 16.2.2二次根式的除法课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 568.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-13 18:58:04 | ||
图片预览






文档简介
(共16张PPT)
16.2 二根次式的乘除
第十六章 二次根式
导入新课
讲授新课
当堂练习
课堂小结
第2课时 二次根式的除法
情境引入
1.理解二次根式的除法则及商的算术平方根的性质.掌握最简二
次根式的特点.(重点)
2.合理简洁地进行二次根式的除法运算.(难点)
导入新课
问题1 设长方形的面积为S,其中一边长为a,则另一边长表示为: ;
问题3 上面列式是什么运算?又该如何计算呢?
二次根式的除法运算
讲授新课
1.计算下列各式:
观察计算结果,你发现什么规律?(请用式子表示这一规律).
(a≥0,b>0)
归纳总结
二次根式的除法法则
首页
文字叙述
算术平方根的商等于被开方数商的算术平方根.
想一想:除式中被开方数b为什么不能等于0?
二次根式的商的算术平方根的性质
把二次根式的除法法则反过来,就得到
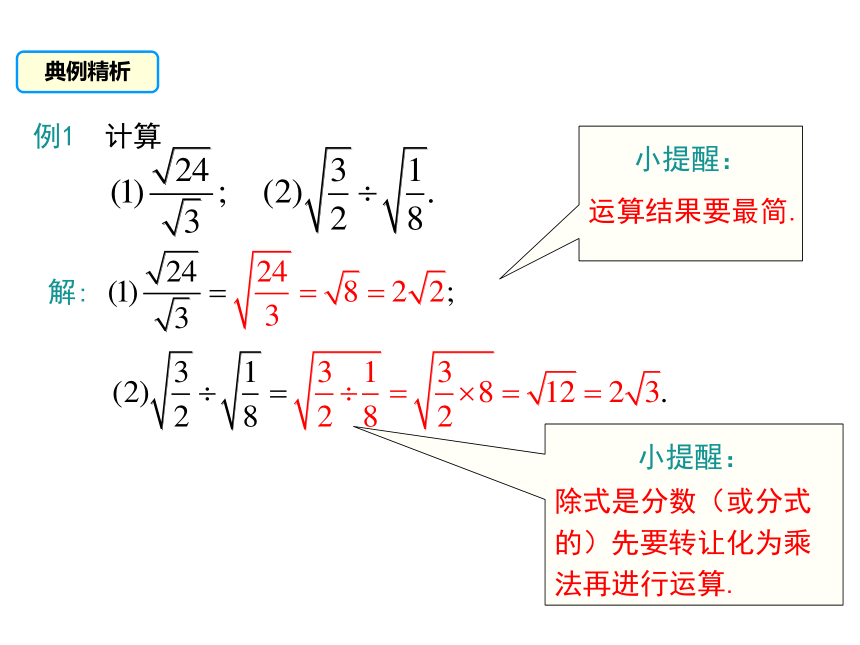
典例精析
例1 计算
解:
小提醒:
运算结果要最简.
小提醒:
除式是分数(或分式的)先要转让化为乘法再进行运算.
归纳总结
二次根式的乘法扩充法则
解:
首页
二次根式的商的算术平方根的性质
类似的,把二次根式的除法法则反过来,就得到
我们知道,把二次根式的乘法法则反过来就得到积的算术平方根的性质.
小提醒:
记住成立的条件!
利用它可以进行二次根式的化简.
例2 化简
解:
典例精析
还有其他解法吗?
补充解法:
分母有理化
把分母中的根号化去,使分母变成有理数的这个过程就叫做分母有理化.
化简:
解:
典例精析
例2 化简
B组:
解:
定义
满足如下两个特点:
(1)被开方数中不含分母;
(2)被开方数中不含能开得尽方的因数或因式
我们把满足上述两个条件的二次根式,叫做最简二次根式.
(简记为:一根号无分母,分母无根号;二不能再开方)
当堂练习
1.计算 的结果是( )
A. 3 B. 5 C. 6 D. 8
A
2.把 分母有理化得( )
A. B. C. D.
D
B
4. 在二次根式 中属于最简二次根式的是 .
5. 已知长方形的面积S=2cm2, 若一边长a= cm,则另一边长b= cm.
6.已知x>y>0,化简:
7.化简:
解:
课堂小结
二次根式除法
法则
性质
拓展法则:
相关概念
分母有理化
最简二次根式
16.2 二根次式的乘除
第十六章 二次根式
导入新课
讲授新课
当堂练习
课堂小结
第2课时 二次根式的除法
情境引入
1.理解二次根式的除法则及商的算术平方根的性质.掌握最简二
次根式的特点.(重点)
2.合理简洁地进行二次根式的除法运算.(难点)
导入新课
问题1 设长方形的面积为S,其中一边长为a,则另一边长表示为: ;
问题3 上面列式是什么运算?又该如何计算呢?
二次根式的除法运算
讲授新课
1.计算下列各式:
观察计算结果,你发现什么规律?(请用式子表示这一规律).
(a≥0,b>0)
归纳总结
二次根式的除法法则
首页
文字叙述
算术平方根的商等于被开方数商的算术平方根.
想一想:除式中被开方数b为什么不能等于0?
二次根式的商的算术平方根的性质
把二次根式的除法法则反过来,就得到
典例精析
例1 计算
解:
小提醒:
运算结果要最简.
小提醒:
除式是分数(或分式的)先要转让化为乘法再进行运算.
归纳总结
二次根式的乘法扩充法则
解:
首页
二次根式的商的算术平方根的性质
类似的,把二次根式的除法法则反过来,就得到
我们知道,把二次根式的乘法法则反过来就得到积的算术平方根的性质.
小提醒:
记住成立的条件!
利用它可以进行二次根式的化简.
例2 化简
解:
典例精析
还有其他解法吗?
补充解法:
分母有理化
把分母中的根号化去,使分母变成有理数的这个过程就叫做分母有理化.
化简:
解:
典例精析
例2 化简
B组:
解:
定义
满足如下两个特点:
(1)被开方数中不含分母;
(2)被开方数中不含能开得尽方的因数或因式
我们把满足上述两个条件的二次根式,叫做最简二次根式.
(简记为:一根号无分母,分母无根号;二不能再开方)
当堂练习
1.计算 的结果是( )
A. 3 B. 5 C. 6 D. 8
A
2.把 分母有理化得( )
A. B. C. D.
D
B
4. 在二次根式 中属于最简二次根式的是 .
5. 已知长方形的面积S=2cm2, 若一边长a= cm,则另一边长b= cm.
6.已知x>y>0,化简:
7.化简:
解:
课堂小结
二次根式除法
法则
性质
拓展法则:
相关概念
分母有理化
最简二次根式
