人教新课标A版 选修4-2 第一讲线性变换与二阶矩阵 一 线性变换与二阶矩阵(43张PPT)
文档属性
| 名称 | 人教新课标A版 选修4-2 第一讲线性变换与二阶矩阵 一 线性变换与二阶矩阵(43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-13 00:00:00 | ||
图片预览









文档简介
(共43张PPT)
了解矩阵的概念
掌握五类特殊的线性变换及其二阶矩阵
用代数方法表示几何变换,进而就可以从代数的角度研究几何变换
体验在直角坐标系中线性变换与二阶矩阵之间的一一对应关系
1.二阶矩阵的概念
2.线性变换及其对应的二阶矩阵
线性变换与二阶矩阵之间的一一对应关系
旋转变换
反射变换
伸缩变换
投影变换
切变变换
(一)几种特殊线性变换及其二阶矩阵
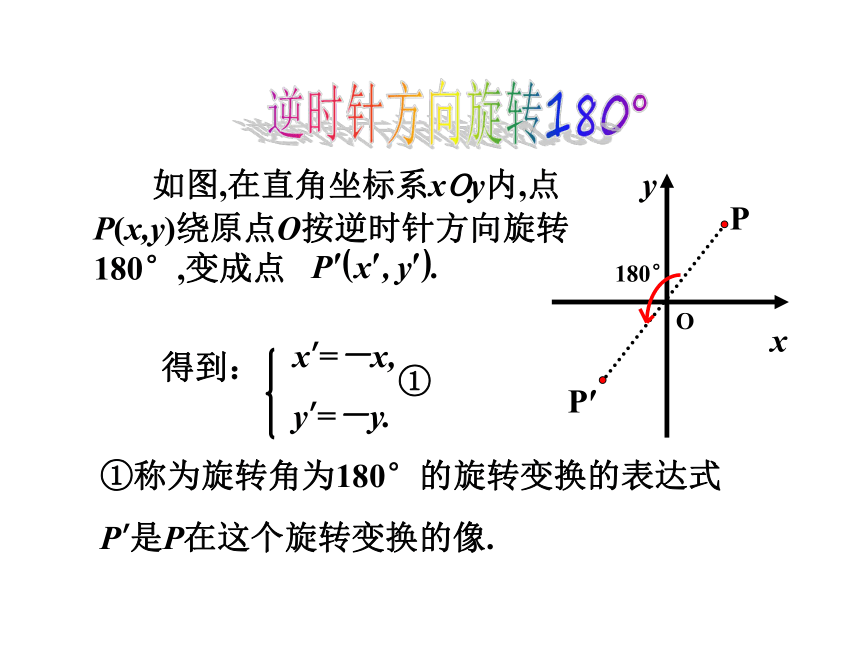
1.旋转变换
①称为旋转角为180°的旋转变换的表达式
P’是P在这个旋转变换的像.
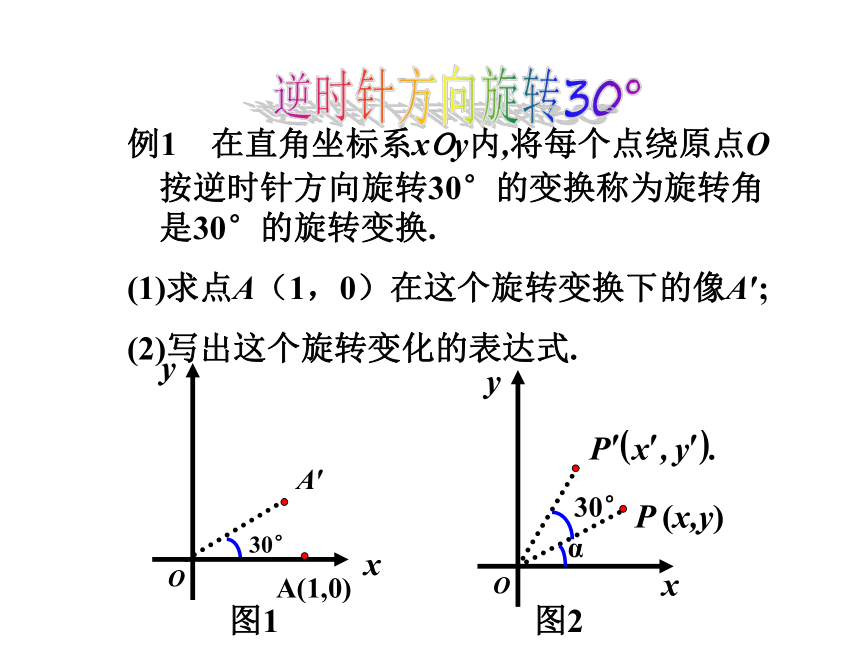
例1 在直角坐标系xoy内,将每个点绕原点O按逆时针方向旋转30°的变换称为旋转角是30°的旋转变换.
求点A(1,0)在这个旋转变换下的像A′;
写出这个旋转变化的表达式.
图1
图2
即:
即得到正方形数表:
由两角和的三角函数公式得:
其中系数a,b,c,d均为常数,则称③的几何变换为线性变换. ③式叫做这个线性变换的坐标变换公式.
在平面直角坐标系xOy中,很多平面变换(平面内有点构成的集合)到它自身的映射都具有下列形式
定义
零矩阵:
记为:
单位矩阵:
记为:
2.反射变换
平面上的任意一点P变成它关于直线l的对称点P’的线性变换叫做关于直线l的反射.
例:在直角坐标系xOy内,任意点P(x,y)关于直线y=x的对称点为P’(x’,y’).则相应
的坐标变换公式是:
对应的二阶矩阵是
3.伸缩变换
在直角坐标系xOy内,将每个点的横坐标变为原来的k1倍,纵坐标变为原来的k2 ,其中k1 ,k2均为非零常数,称这样的几何变换为伸缩变换.
定义
伸缩变换的坐标变换公式为:
对应的二阶矩阵:
4.投影变换
设l是一条给定的直线.对平面内任意一点P作直线l的垂线,垂足为P’,称点P’为点P在直线l上的投影.
平面上每一点P变成它在直线l上的投影P’,这个变换称为关与直线l的投影变换.
定义
在直角坐标系xOy内,任意点P关于x轴的投影变换的坐标变换公式为:
对应的二阶矩阵:
5.切变变换
如图,在直角坐标系xOy内,将每一点P(x,y)沿与x轴平行的方向平移ky各单位变成P’,其中k为常数,称这类变换为平行于x轴的切变变换.
定义
平行与x轴的切变变换的坐标变换公式为:
对应的二阶矩阵:
平行于y轴的切变变换的坐标公式?
对应的二阶矩阵:
(二)变换、矩阵的相等
即:
对应的二阶矩阵:
即:
即:
即:
对应的二阶矩阵:
1.旋转变换的坐标变换公式
2.对应的二阶矩阵
1.旋转角度
设σ,ρ是同一直角坐标平面内的两个线性变换.若对平面内任意点P,都有σ(P)= ρ(P),则这两个线性变换相等,记为σ=ρ.
定义
设σ,ρ所对应的二阶矩阵分别为
A= ,B= .若σ=ρ,
则a1=a2,b1=b2,c1=c2,d1=d2.这时我们称二阶
矩阵A与二阶矩阵B相等.
定义
解:由矩阵定义:
1.几种特殊的线性变换:旋转变换、反射变换、伸缩变换、投影变换、切变变换
(要求:理解并掌握各变换所对应的坐标变换公式及其对应的二阶矩阵.)
2.变换和矩阵的相等
(1)变换相等:对应坐标变换公式和二阶矩阵相等
(2)矩阵相等:对应系数相等
注:两个线性变换相等当且仅当对应的 二阶矩阵相等
1.(1)坐标变换公式为:
对应的二阶矩阵:
(2)坐标变换公式为:
对应的二阶矩阵:
(2)设P(x,y)是平面直角坐标系xOy内的任意一点,则它在这个变换下的像为P’(x+y,0),因此,坐标变换公式是
对应的二阶矩阵是
5.由X = Y,得x = 3 , y =-9 , z = 0.
6.设P(x0 , y0)是平面直角坐标系xOy内的任意一点,它关于直线l:y=2x的投影变换下的像为P’(x’,y’).
易得:过点P(x0,y0)垂直于直线的斜率为k=-1/2.于是,直线方程为:
解方程组:
得直线l:y=2x与直线y-y0=-1/2(x-x0)的坐标((x0+2y0)/5,(2x0+4y0)/5).
∵M是线段PP’的中点,所以
即:
∴坐标变换公式:
对应的二阶矩阵:
(2)对应的坐标变换公式:
对应的二阶矩阵:
了解矩阵的概念
掌握五类特殊的线性变换及其二阶矩阵
用代数方法表示几何变换,进而就可以从代数的角度研究几何变换
体验在直角坐标系中线性变换与二阶矩阵之间的一一对应关系
1.二阶矩阵的概念
2.线性变换及其对应的二阶矩阵
线性变换与二阶矩阵之间的一一对应关系
旋转变换
反射变换
伸缩变换
投影变换
切变变换
(一)几种特殊线性变换及其二阶矩阵
1.旋转变换
①称为旋转角为180°的旋转变换的表达式
P’是P在这个旋转变换的像.
例1 在直角坐标系xoy内,将每个点绕原点O按逆时针方向旋转30°的变换称为旋转角是30°的旋转变换.
求点A(1,0)在这个旋转变换下的像A′;
写出这个旋转变化的表达式.
图1
图2
即:
即得到正方形数表:
由两角和的三角函数公式得:
其中系数a,b,c,d均为常数,则称③的几何变换为线性变换. ③式叫做这个线性变换的坐标变换公式.
在平面直角坐标系xOy中,很多平面变换(平面内有点构成的集合)到它自身的映射都具有下列形式
定义
零矩阵:
记为:
单位矩阵:
记为:
2.反射变换
平面上的任意一点P变成它关于直线l的对称点P’的线性变换叫做关于直线l的反射.
例:在直角坐标系xOy内,任意点P(x,y)关于直线y=x的对称点为P’(x’,y’).则相应
的坐标变换公式是:
对应的二阶矩阵是
3.伸缩变换
在直角坐标系xOy内,将每个点的横坐标变为原来的k1倍,纵坐标变为原来的k2 ,其中k1 ,k2均为非零常数,称这样的几何变换为伸缩变换.
定义
伸缩变换的坐标变换公式为:
对应的二阶矩阵:
4.投影变换
设l是一条给定的直线.对平面内任意一点P作直线l的垂线,垂足为P’,称点P’为点P在直线l上的投影.
平面上每一点P变成它在直线l上的投影P’,这个变换称为关与直线l的投影变换.
定义
在直角坐标系xOy内,任意点P关于x轴的投影变换的坐标变换公式为:
对应的二阶矩阵:
5.切变变换
如图,在直角坐标系xOy内,将每一点P(x,y)沿与x轴平行的方向平移ky各单位变成P’,其中k为常数,称这类变换为平行于x轴的切变变换.
定义
平行与x轴的切变变换的坐标变换公式为:
对应的二阶矩阵:
平行于y轴的切变变换的坐标公式?
对应的二阶矩阵:
(二)变换、矩阵的相等
即:
对应的二阶矩阵:
即:
即:
即:
对应的二阶矩阵:
1.旋转变换的坐标变换公式
2.对应的二阶矩阵
1.旋转角度
设σ,ρ是同一直角坐标平面内的两个线性变换.若对平面内任意点P,都有σ(P)= ρ(P),则这两个线性变换相等,记为σ=ρ.
定义
设σ,ρ所对应的二阶矩阵分别为
A= ,B= .若σ=ρ,
则a1=a2,b1=b2,c1=c2,d1=d2.这时我们称二阶
矩阵A与二阶矩阵B相等.
定义
解:由矩阵定义:
1.几种特殊的线性变换:旋转变换、反射变换、伸缩变换、投影变换、切变变换
(要求:理解并掌握各变换所对应的坐标变换公式及其对应的二阶矩阵.)
2.变换和矩阵的相等
(1)变换相等:对应坐标变换公式和二阶矩阵相等
(2)矩阵相等:对应系数相等
注:两个线性变换相等当且仅当对应的 二阶矩阵相等
1.(1)坐标变换公式为:
对应的二阶矩阵:
(2)坐标变换公式为:
对应的二阶矩阵:
(2)设P(x,y)是平面直角坐标系xOy内的任意一点,则它在这个变换下的像为P’(x+y,0),因此,坐标变换公式是
对应的二阶矩阵是
5.由X = Y,得x = 3 , y =-9 , z = 0.
6.设P(x0 , y0)是平面直角坐标系xOy内的任意一点,它关于直线l:y=2x的投影变换下的像为P’(x’,y’).
易得:过点P(x0,y0)垂直于直线的斜率为k=-1/2.于是,直线方程为:
解方程组:
得直线l:y=2x与直线y-y0=-1/2(x-x0)的坐标((x0+2y0)/5,(2x0+4y0)/5).
∵M是线段PP’的中点,所以
即:
∴坐标变换公式:
对应的二阶矩阵:
(2)对应的坐标变换公式:
对应的二阶矩阵:
