人教新课标A版 选修4-2 第二讲变换的复合与二阶矩阵的乘法 一 复合变换与二阶矩阵的乘法(32张PPT)
文档属性
| 名称 | 人教新课标A版 选修4-2 第二讲变换的复合与二阶矩阵的乘法 一 复合变换与二阶矩阵的乘法(32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-13 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
直角坐标系中,连续进行两次线性变换,其作用效果是否能用一个线性变换来表示?
是否存在一个二阶矩阵与之对应?
若存在,这个线性变换的二阶矩阵与原来两个线性变换的二阶矩阵由什么关系?
掌握矩阵乘积的概念;
了解矩阵乘法的运算律,并能灵活应用.
通过从特殊到一般,从具体到抽象的过程,理解一般性的概念和结论.
培养学生抽象思维能力.
重点:
难点:
1.矩阵乘积的概念;
2.矩阵乘法的运算律.
1.矩阵乘积的概念;
2.矩阵乘法的运算律.
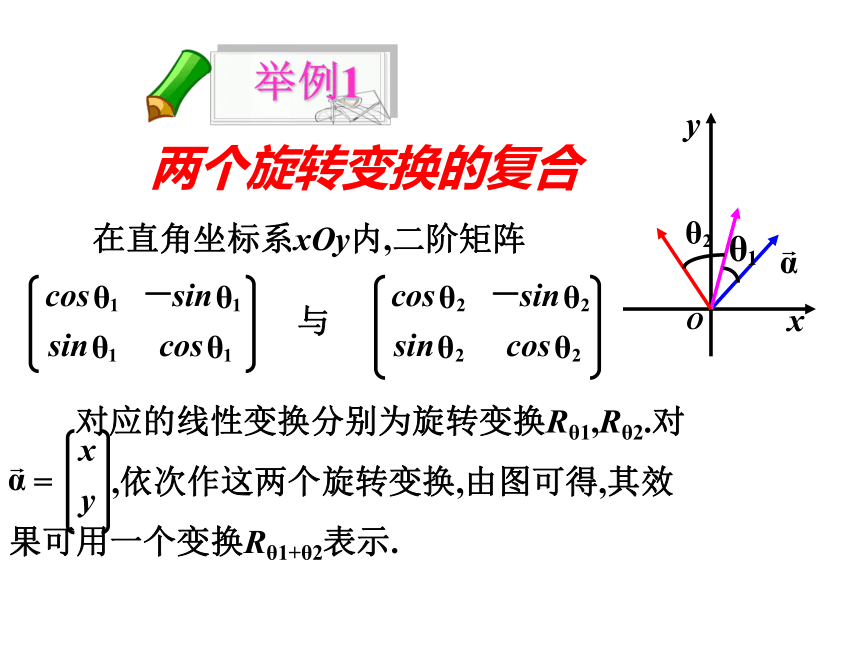
两个旋转变换的复合
两个线性变换的复合仍然是线性变换
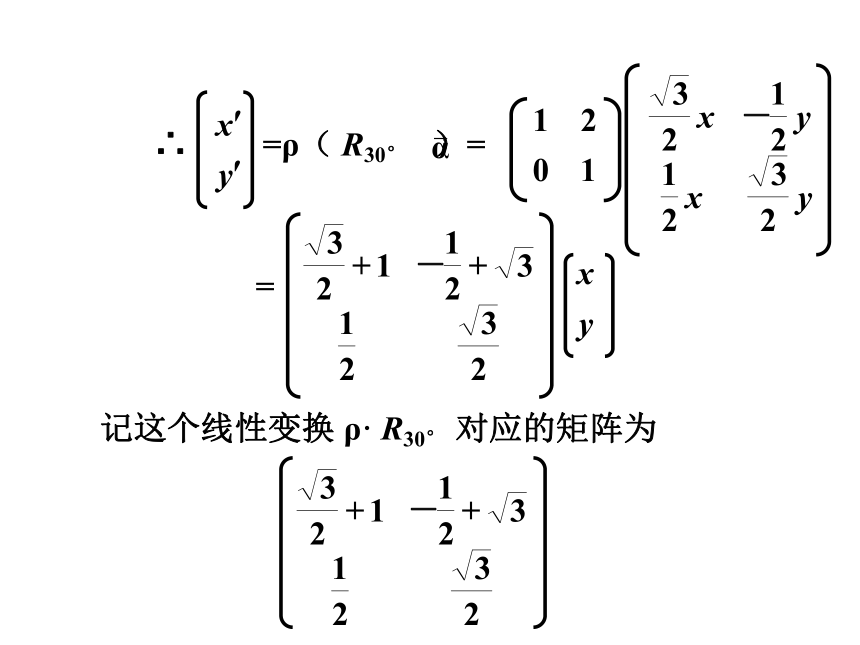
记这个线性变换 ρ· R30° 对应的矩阵为
上述这个线性变换就称为变换g和变换f的复合变换,记为f·g.
复合变换f·g对应的矩阵为
称这个矩阵为矩阵A与B的乘积,记为AB
一一
对应
特殊线性变换的复合
复合前后矩阵的关系
线性变换的复合与二阶矩阵的乘积
两个线性变换的复合变换仍然是线性变换;
两个线性变换的复合变换的二阶矩阵是原来两个线性变换的“乘积”.
矩阵乘法的内在规律:
矩阵AB第一行的第一个元素等于A的第一行的元素与B的第一列的元素的乘积之和;
矩阵AB第一行的第二个元素等于A的第一行的元素与B的第二列的元素的乘积之和;
矩阵AB第二行的第一个元素等于A的第二行的元素与B的第一列的元素的乘积之和;
矩阵AB第二行的第二个元素等于A的第二行的元素与B的第二列的元素的乘积之和.
线性变换f·g的复合顺序:先做线性变换g再做线性变换f.
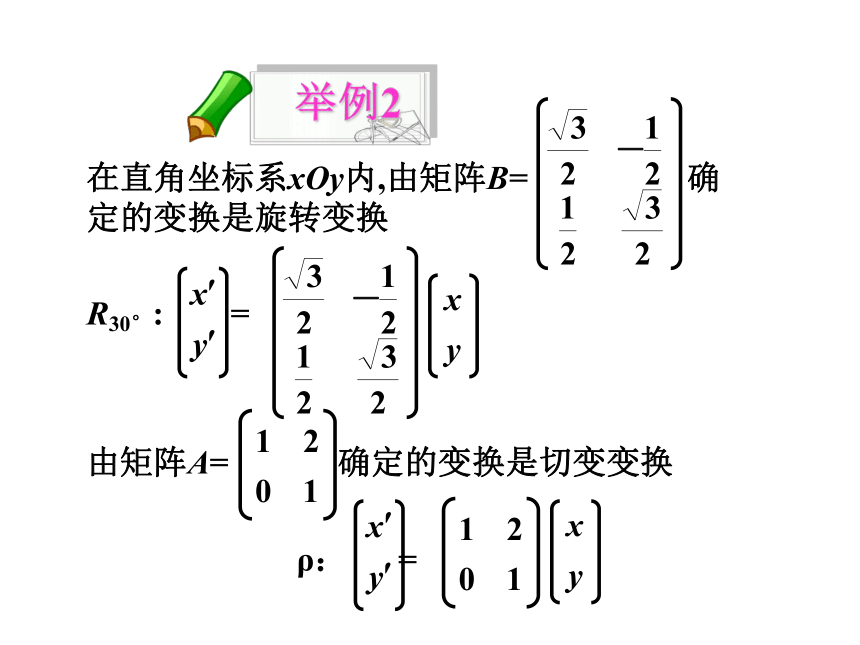
解:
=
(3)
∴可得到:
3.用矩阵的乘积证明下面等式
直角坐标系中,连续进行两次线性变换,其作用效果是否能用一个线性变换来表示?
是否存在一个二阶矩阵与之对应?
若存在,这个线性变换的二阶矩阵与原来两个线性变换的二阶矩阵由什么关系?
掌握矩阵乘积的概念;
了解矩阵乘法的运算律,并能灵活应用.
通过从特殊到一般,从具体到抽象的过程,理解一般性的概念和结论.
培养学生抽象思维能力.
重点:
难点:
1.矩阵乘积的概念;
2.矩阵乘法的运算律.
1.矩阵乘积的概念;
2.矩阵乘法的运算律.
两个旋转变换的复合
两个线性变换的复合仍然是线性变换
记这个线性变换 ρ· R30° 对应的矩阵为
上述这个线性变换就称为变换g和变换f的复合变换,记为f·g.
复合变换f·g对应的矩阵为
称这个矩阵为矩阵A与B的乘积,记为AB
一一
对应
特殊线性变换的复合
复合前后矩阵的关系
线性变换的复合与二阶矩阵的乘积
两个线性变换的复合变换仍然是线性变换;
两个线性变换的复合变换的二阶矩阵是原来两个线性变换的“乘积”.
矩阵乘法的内在规律:
矩阵AB第一行的第一个元素等于A的第一行的元素与B的第一列的元素的乘积之和;
矩阵AB第一行的第二个元素等于A的第一行的元素与B的第二列的元素的乘积之和;
矩阵AB第二行的第一个元素等于A的第二行的元素与B的第一列的元素的乘积之和;
矩阵AB第二行的第二个元素等于A的第二行的元素与B的第二列的元素的乘积之和.
线性变换f·g的复合顺序:先做线性变换g再做线性变换f.
解:
=
(3)
∴可得到:
3.用矩阵的乘积证明下面等式
