人教新课标A版 选修4-2 第一讲线性变换与二阶矩阵 二 二阶矩阵与平面向量的乘法(24张PPT)
文档属性
| 名称 | 人教新课标A版 选修4-2 第一讲线性变换与二阶矩阵 二 二阶矩阵与平面向量的乘法(24张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 694.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-13 21:26:18 | ||
图片预览





文档简介
(共24张PPT)
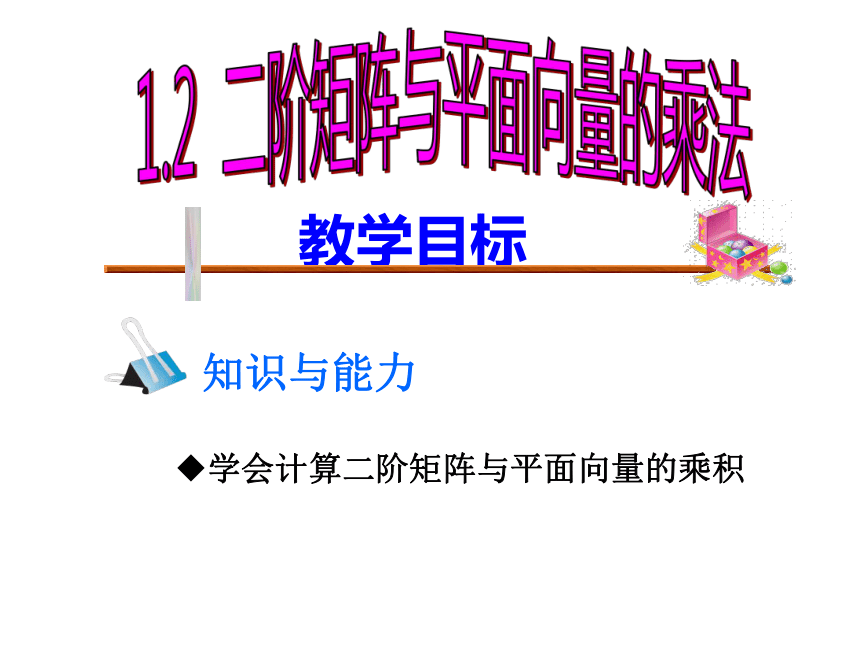
平面直角坐标系xOy内,任意点A(x,y)
点A(x,y)
有序实
数对(x,y)
一一对应
应对一一
应对一一
通过上一节的学习,我们知道线性变换和二阶矩阵是一一对应的.那么能否用二阶矩阵表示线性变换呢?
学会计算二阶矩阵与平面向量的乘积
以变换的观点认识矩阵与向量乘法的意义.
培养学生的反向思维,进一步搞清二阶矩阵与线性变换之间的联系.
二阶矩阵与平面向量的乘积.
以变换的观点认识矩阵与向量乘法的意义.
规定:所有平面向量都写成列向量的形式.
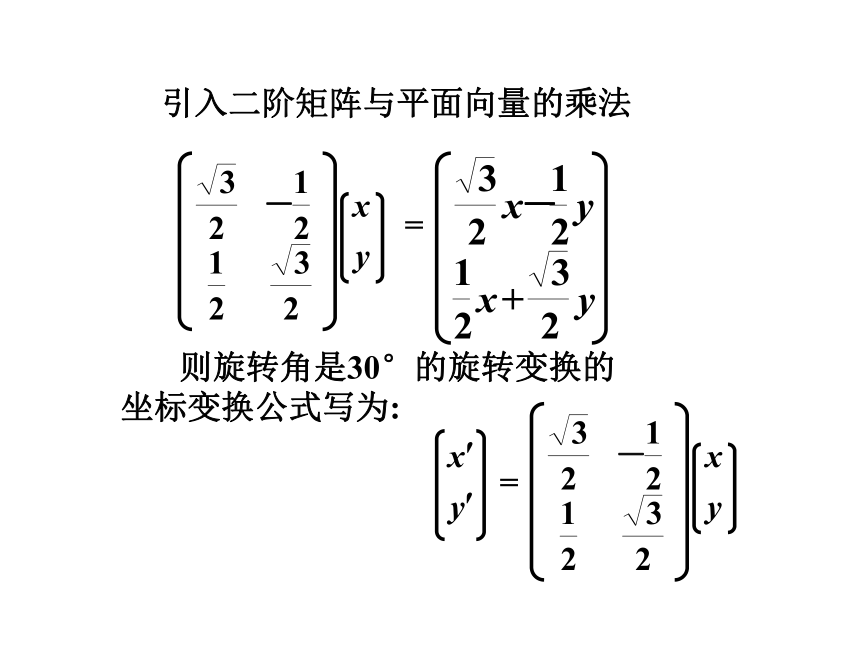
由上一节知道旋转角是30°的旋转变换公式是:
引入二阶矩阵与平面向量的乘法
则旋转角是30°的旋转变换的坐标变换公式写为:
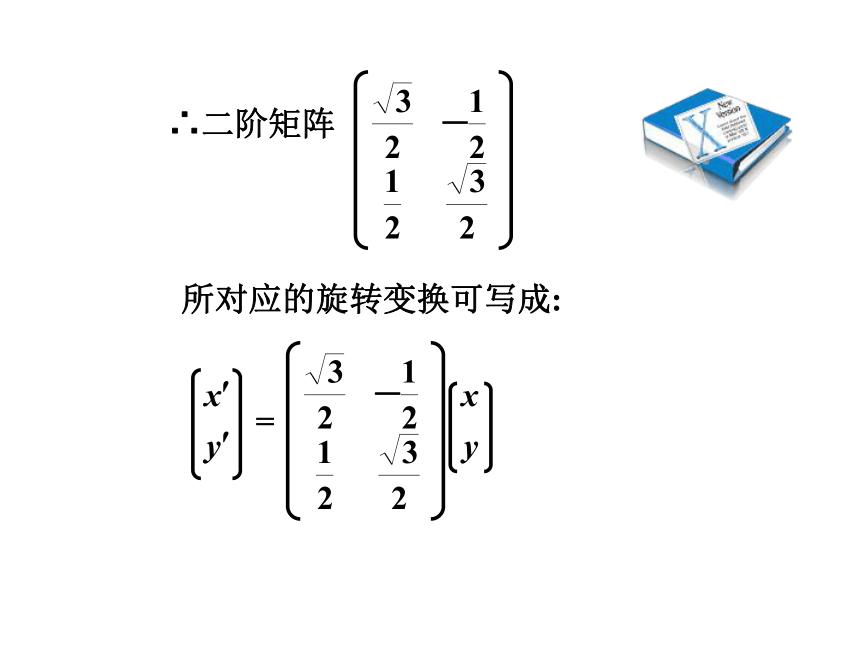
∴二阶矩阵
所对应的旋转变换可写成:
思考题的答案:
能用二阶矩阵表示线性变换
任何一个线性变换
都可表示成
实现了用二阶矩阵和平面向量的乘积来表示线性变换的目的.
好棒噢
1.不能.
则:
解得:
即矩阵M对应的线性变换把点C变成点(8/5,-2/5)
→
o⊙⊙
平面直角坐标系xOy内,任意点A(x,y)
点A(x,y)
有序实
数对(x,y)
一一对应
应对一一
应对一一
通过上一节的学习,我们知道线性变换和二阶矩阵是一一对应的.那么能否用二阶矩阵表示线性变换呢?
学会计算二阶矩阵与平面向量的乘积
以变换的观点认识矩阵与向量乘法的意义.
培养学生的反向思维,进一步搞清二阶矩阵与线性变换之间的联系.
二阶矩阵与平面向量的乘积.
以变换的观点认识矩阵与向量乘法的意义.
规定:所有平面向量都写成列向量的形式.
由上一节知道旋转角是30°的旋转变换公式是:
引入二阶矩阵与平面向量的乘法
则旋转角是30°的旋转变换的坐标变换公式写为:
∴二阶矩阵
所对应的旋转变换可写成:
思考题的答案:
能用二阶矩阵表示线性变换
任何一个线性变换
都可表示成
实现了用二阶矩阵和平面向量的乘积来表示线性变换的目的.
好棒噢
1.不能.
则:
解得:
即矩阵M对应的线性变换把点C变成点(8/5,-2/5)
→
o⊙⊙
