湘教版2020年八年级数学下册1.3 直角三角形全等的判定课件(42张)
文档属性
| 名称 | 湘教版2020年八年级数学下册1.3 直角三角形全等的判定课件(42张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-13 15:58:55 | ||
图片预览











文档简介
(共42张PPT)
1.3 直角三角形全等的判定
【知识再现】
1.形状和大小完全相等的两个三角形叫_______
三角形.?
2.证明三角形全等的定理有:AAS,________,SSS, ______.?
全等
ASA
SAS
【新知预习】阅读教材P19-20,完成探究并归纳结论:
1.(1)“HL”中“H”代表什么?“L”代表什么?“HL”表示的是什么意思?
(2)如何验证“HL”可以判定两个三角形全等?
(3)到目前为止,我们学习了几种三角形全等的判别方法?各是什么?那么对于直角三角形全等的判别方法有几种?
解:(1)斜边;直角边;斜边和一条直角边对应相等的两个直角三角形全等.
(2)利用勾股定理求出另一直角边长,然后利用SSS证明.
(3)4种;分别是AAS,ASA,SSS,SAS;直角三角形全等的判定方法有AAS,ASA,SSS,SAS,HL,5种.
2.运用“HL”证明直角三角形全等通常写成什么格式?
通常写成下面的格式:
在Rt△ABC与Rt△DEF中,
∵
∴Rt△ABC≌Rt△DEF(HL).
【基础小练】
请自我检测一下预习的效果吧!
1.(2019·黔南州期末)如图,BE=CF,AE⊥BC,
DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则
还需要添加一个条件是 ( )
D
A.AE=DF B.∠A=∠D
C.∠B=∠C D.AB=DC
2.如图,AB⊥AC于A,BD⊥CD于D,若AC=DB,则下列
结论中不正确的是 ( )
C
A.∠A=∠D
B.∠ABC=∠DCB
C.OB=OD
D.OA=OD
知识点一 用“HL”证明直角三角形全等
(P20例1拓展)
【典例1】如图,在△ABC和△DCB中,
∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB.
(2)△OBC是何种三角形?证明你的结论.
【自主解答】(1)在△ABC和△DCB中,∠A=∠D=90°,AC=BD,BC为公共边,
∴Rt△ABC≌Rt△DCB(HL).
(2)△OBC是等腰三角形.
∵Rt△ABC≌Rt△DCB,
∴∠ACB=∠DBC,
∴OB=OC,
∴△OBC是等腰三角形.
【学霸提醒】
应用“HL”定理的两个误区
1.用“HL”定理证明三角形全等的前提是在直角三角形中,在一般三角形中不能应用.
2.不能把“HL”定理错误地认为是应用“SSA”.
【题组训练】
1.(2019·蔡甸区期末)如图,BE,CD是△ABC的高,且
BD=EC,判定△BCD≌△CBE的依据是“_______”.?
HL
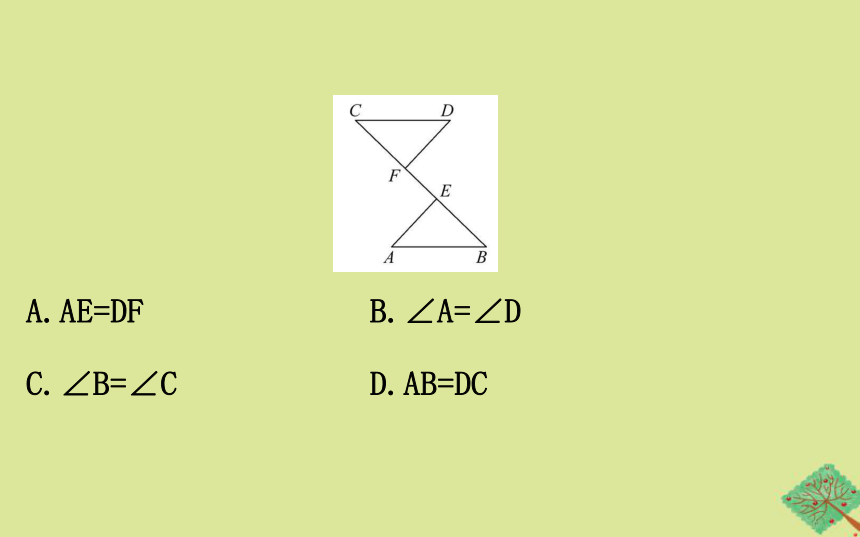
★★2.如图,点C,E,B,F在一条直线上,AB⊥CF于点B,DE⊥CF于点E,AC=DF,AB=DE.求证:CE=BF..
【解题指南】解答本题的两个关键
1.利用“HL”证明Rt△ABC≌Rt△DEF.
2.根据全等三角形的性质和等式的性质解题.
证明:∵AB⊥CF,DE⊥CF,
∴∠ABC=∠DEF=90°.
在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL),∴BC=EF,
∴BC-BE=EF-BE,即CE=BF.
知识点二 直角三角形全等的应用(P20例2拓展)
【典例2】已知:线段c,直线l及l外一点A.
求作:Rt△ABC,使直角边AC(AC⊥l,垂足为点C),斜边AB=c.(用尺规作图,写出结论,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑).
【自主解答】如图所示:
(规范作图)
则Rt△ABC就是所求作的三角形.(写出结论)
【学霸提醒】
常见尺规作直角三角形的三种方法
1.已知斜边和一条直角边:作直角,截取一直角边,然后以直角边的端点为圆心,以斜边长为半径画弧,交另一直角边于一点,连接即可.
2.已知斜边与一锐角:作一条线段等于斜边,以斜边的一个端点为顶点作等于给定锐角的角,然后过斜边另一端点作锐角另一边的垂线即可.
3.已知两直角边:作直角,在其两边分别截取两段等于给定直角边长度的线段,连接即可.
【题组训练】
1.在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,
如图,那么下列各条件中,不能使
Rt△ABC≌Rt△A′B′C′的是 ( )
B
A.AB=A′B′=5,BC=B′C′=3
B.AB=B′C′=5,∠A=∠B′=40°
C.AC=A′C′=5,BC=B′C′=3
D.AC=A′C′=5,∠A=∠A′=40°
★2.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与
BE相交于点F,若BF=AC,则∠ABC=_______度.
45
★3.如图,AB=DE,∠A=∠D=90°,那么要得到
△ABC≌△DEF,可以添加一个条件是________,
△ABC与△DEF全等的理由是____________________.?
AC=DF
SAS(答案不唯一)
★★4.如图所示,已知线段AB,请你以点A为直角顶点,利用尺规作图作Rt△ACD,使得点C在线段AB的延长线上且AC=2AB,另一条直角边AD=AB.(保留作图痕迹,不写作法)
解:如图所示,△ACD即为所求.
【火眼金睛】
如图,已知∠B=∠ACD,∠ACB=∠D=90°,AC是△ABC和△ACD的公共边,所以就可以证明△ABC和△ACD全等.你认为正确吗?为什么?
【正解】不正确,理由如下:
因为∠B=∠ACD,但对应边AC≠AD,
所以△ABC和△ACD不全等.
【一题多变】
如图,已知CE⊥AB,DF⊥AB,AC=BD,CE=DF,求证:AC∥BD.
证明:∵CE⊥AB,DF⊥AB,
∴∠CEA=∠DFB=90°.
又∵AC=BD,CE=DF,
∴Rt△ACE≌Rt△BDF(HL).
∴∠A=∠B,∴AC∥BD.
【母题变式】
【变式一】(变换条件)如图所示,AB⊥BC,DC⊥AC,垂足分别为B,C,过D点作BC的垂线交BC于F,交AC于E,AB=EC,试判断AC和ED的长度有什么关系,并说明理由. .
解:AC=ED,理由如下:
∵AB⊥BC,DC⊥AC,ED⊥BC,
∴∠B=∠EFC=∠DCE=90°.
∴∠A+∠ACB=90°,∠CEF+∠ACB=90°.
∴∠A=∠CEF.
在△ABC和△ECD中,
∴△ABC≌△ECD.∴AC=ED.
【变式二】(变换条件和问法)上题中,若把AB=EC改为AB=CF,判断AC与CD的数量关系,并说明理由.
解:AC=CD,理由如下:∵AB⊥BC, ED⊥BC,DC⊥AC,∴∠B=∠CFD=∠DCE=90°,
∴∠A+∠ACB=90°,∠ACB+∠DCF=90°,
∴∠A=∠DCF,
在△ABC和△CFD中,
∴△ABC≌△CFD.∴AC=CD.
1.3 直角三角形全等的判定
【知识再现】
1.形状和大小完全相等的两个三角形叫_______
三角形.?
2.证明三角形全等的定理有:AAS,________,SSS, ______.?
全等
ASA
SAS
【新知预习】阅读教材P19-20,完成探究并归纳结论:
1.(1)“HL”中“H”代表什么?“L”代表什么?“HL”表示的是什么意思?
(2)如何验证“HL”可以判定两个三角形全等?
(3)到目前为止,我们学习了几种三角形全等的判别方法?各是什么?那么对于直角三角形全等的判别方法有几种?
解:(1)斜边;直角边;斜边和一条直角边对应相等的两个直角三角形全等.
(2)利用勾股定理求出另一直角边长,然后利用SSS证明.
(3)4种;分别是AAS,ASA,SSS,SAS;直角三角形全等的判定方法有AAS,ASA,SSS,SAS,HL,5种.
2.运用“HL”证明直角三角形全等通常写成什么格式?
通常写成下面的格式:
在Rt△ABC与Rt△DEF中,
∵
∴Rt△ABC≌Rt△DEF(HL).
【基础小练】
请自我检测一下预习的效果吧!
1.(2019·黔南州期末)如图,BE=CF,AE⊥BC,
DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则
还需要添加一个条件是 ( )
D
A.AE=DF B.∠A=∠D
C.∠B=∠C D.AB=DC
2.如图,AB⊥AC于A,BD⊥CD于D,若AC=DB,则下列
结论中不正确的是 ( )
C
A.∠A=∠D
B.∠ABC=∠DCB
C.OB=OD
D.OA=OD
知识点一 用“HL”证明直角三角形全等
(P20例1拓展)
【典例1】如图,在△ABC和△DCB中,
∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB.
(2)△OBC是何种三角形?证明你的结论.
【自主解答】(1)在△ABC和△DCB中,∠A=∠D=90°,AC=BD,BC为公共边,
∴Rt△ABC≌Rt△DCB(HL).
(2)△OBC是等腰三角形.
∵Rt△ABC≌Rt△DCB,
∴∠ACB=∠DBC,
∴OB=OC,
∴△OBC是等腰三角形.
【学霸提醒】
应用“HL”定理的两个误区
1.用“HL”定理证明三角形全等的前提是在直角三角形中,在一般三角形中不能应用.
2.不能把“HL”定理错误地认为是应用“SSA”.
【题组训练】
1.(2019·蔡甸区期末)如图,BE,CD是△ABC的高,且
BD=EC,判定△BCD≌△CBE的依据是“_______”.?
HL
★★2.如图,点C,E,B,F在一条直线上,AB⊥CF于点B,DE⊥CF于点E,AC=DF,AB=DE.求证:CE=BF..
【解题指南】解答本题的两个关键
1.利用“HL”证明Rt△ABC≌Rt△DEF.
2.根据全等三角形的性质和等式的性质解题.
证明:∵AB⊥CF,DE⊥CF,
∴∠ABC=∠DEF=90°.
在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL),∴BC=EF,
∴BC-BE=EF-BE,即CE=BF.
知识点二 直角三角形全等的应用(P20例2拓展)
【典例2】已知:线段c,直线l及l外一点A.
求作:Rt△ABC,使直角边AC(AC⊥l,垂足为点C),斜边AB=c.(用尺规作图,写出结论,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑).
【自主解答】如图所示:
(规范作图)
则Rt△ABC就是所求作的三角形.(写出结论)
【学霸提醒】
常见尺规作直角三角形的三种方法
1.已知斜边和一条直角边:作直角,截取一直角边,然后以直角边的端点为圆心,以斜边长为半径画弧,交另一直角边于一点,连接即可.
2.已知斜边与一锐角:作一条线段等于斜边,以斜边的一个端点为顶点作等于给定锐角的角,然后过斜边另一端点作锐角另一边的垂线即可.
3.已知两直角边:作直角,在其两边分别截取两段等于给定直角边长度的线段,连接即可.
【题组训练】
1.在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,
如图,那么下列各条件中,不能使
Rt△ABC≌Rt△A′B′C′的是 ( )
B
A.AB=A′B′=5,BC=B′C′=3
B.AB=B′C′=5,∠A=∠B′=40°
C.AC=A′C′=5,BC=B′C′=3
D.AC=A′C′=5,∠A=∠A′=40°
★2.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与
BE相交于点F,若BF=AC,则∠ABC=_______度.
45
★3.如图,AB=DE,∠A=∠D=90°,那么要得到
△ABC≌△DEF,可以添加一个条件是________,
△ABC与△DEF全等的理由是____________________.?
AC=DF
SAS(答案不唯一)
★★4.如图所示,已知线段AB,请你以点A为直角顶点,利用尺规作图作Rt△ACD,使得点C在线段AB的延长线上且AC=2AB,另一条直角边AD=AB.(保留作图痕迹,不写作法)
解:如图所示,△ACD即为所求.
【火眼金睛】
如图,已知∠B=∠ACD,∠ACB=∠D=90°,AC是△ABC和△ACD的公共边,所以就可以证明△ABC和△ACD全等.你认为正确吗?为什么?
【正解】不正确,理由如下:
因为∠B=∠ACD,但对应边AC≠AD,
所以△ABC和△ACD不全等.
【一题多变】
如图,已知CE⊥AB,DF⊥AB,AC=BD,CE=DF,求证:AC∥BD.
证明:∵CE⊥AB,DF⊥AB,
∴∠CEA=∠DFB=90°.
又∵AC=BD,CE=DF,
∴Rt△ACE≌Rt△BDF(HL).
∴∠A=∠B,∴AC∥BD.
【母题变式】
【变式一】(变换条件)如图所示,AB⊥BC,DC⊥AC,垂足分别为B,C,过D点作BC的垂线交BC于F,交AC于E,AB=EC,试判断AC和ED的长度有什么关系,并说明理由. .
解:AC=ED,理由如下:
∵AB⊥BC,DC⊥AC,ED⊥BC,
∴∠B=∠EFC=∠DCE=90°.
∴∠A+∠ACB=90°,∠CEF+∠ACB=90°.
∴∠A=∠CEF.
在△ABC和△ECD中,
∴△ABC≌△ECD.∴AC=ED.
【变式二】(变换条件和问法)上题中,若把AB=EC改为AB=CF,判断AC与CD的数量关系,并说明理由.
解:AC=CD,理由如下:∵AB⊥BC, ED⊥BC,DC⊥AC,∴∠B=∠CFD=∠DCE=90°,
∴∠A+∠ACB=90°,∠ACB+∠DCF=90°,
∴∠A=∠DCF,
在△ABC和△CFD中,
∴△ABC≌△CFD.∴AC=CD.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
