2020版八年级数学下册2.4三角形的中位线课件(29张ppt)(新版)湘教版
文档属性
| 名称 | 2020版八年级数学下册2.4三角形的中位线课件(29张ppt)(新版)湘教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-13 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
2.4 三角形的中位线
【知识再现】
三角形的一个顶点与对边中点的连线叫三角形的中线.
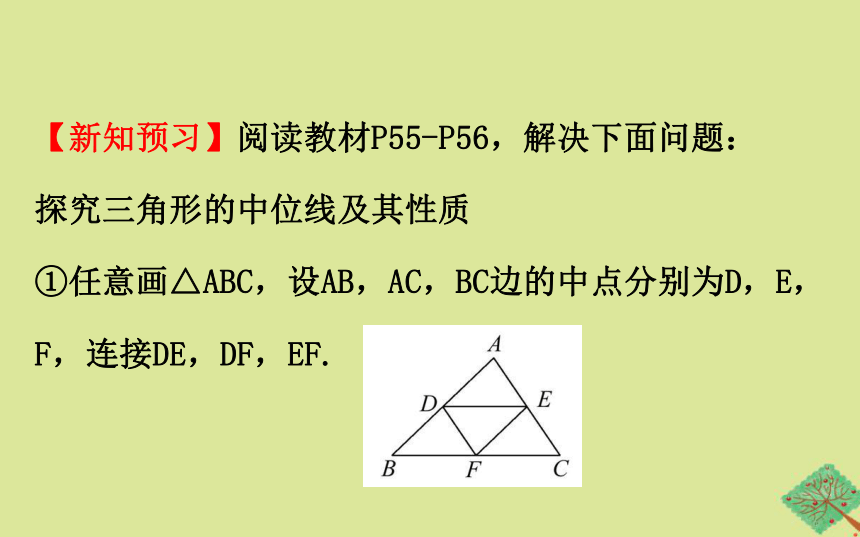
【新知预习】阅读教材P55-P56,解决下面问题:
探究三角形的中位线及其性质
①任意画△ABC,设AB,AC,BC边的中点分别为D,E,F,连接DE,DF,EF.
定义:连接三角形两边的_________的线段,叫作三角
形的中位线,?
②三角形有______条中位线.?
③在图中分别度量∠ADE与∠B的大小,则∠ADE
______∠B,所以DE_______BC.分别量出线段DE与BC的
长,你发现DE=_________.?
中点
3
=
∥
? BC
④对于△ABC其他的两条中位线,重复③中的操作.
你发现的规律:
三角形的中位线_________于第三边,并且等于
_________________.?
平行
第三边的一半
【基础小练】
请自我检测一下预习的效果吧!
1.如图,在△ABC中,AB=8,∠C=90°,∠A=30°,
DE是中位线,则DE的长为 ( )
A
A.2 B.3
C.4 D.2
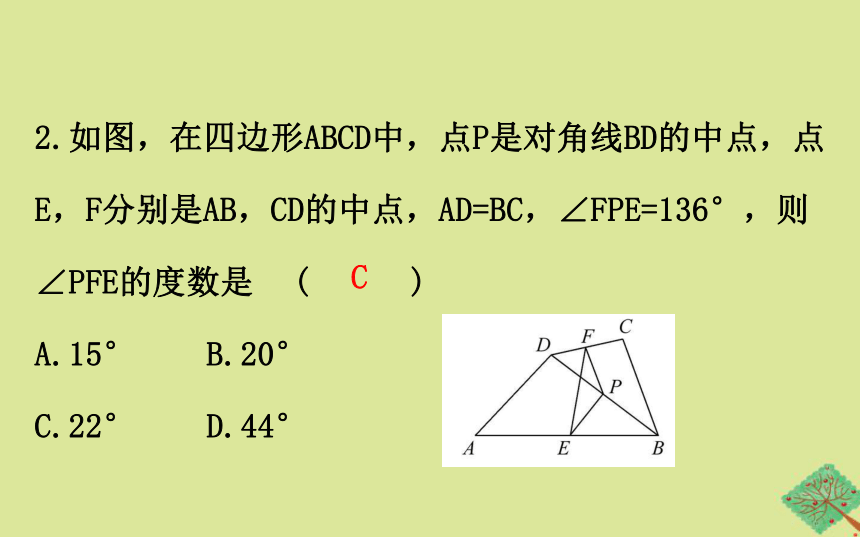
2.如图,在四边形ABCD中,点P是对角线BD的中点,点
E,F分别是AB,CD的中点,AD=BC,∠FPE=136°,则
∠PFE的度数是 ( )
A.15° B.20°
C.22° D.44°
C
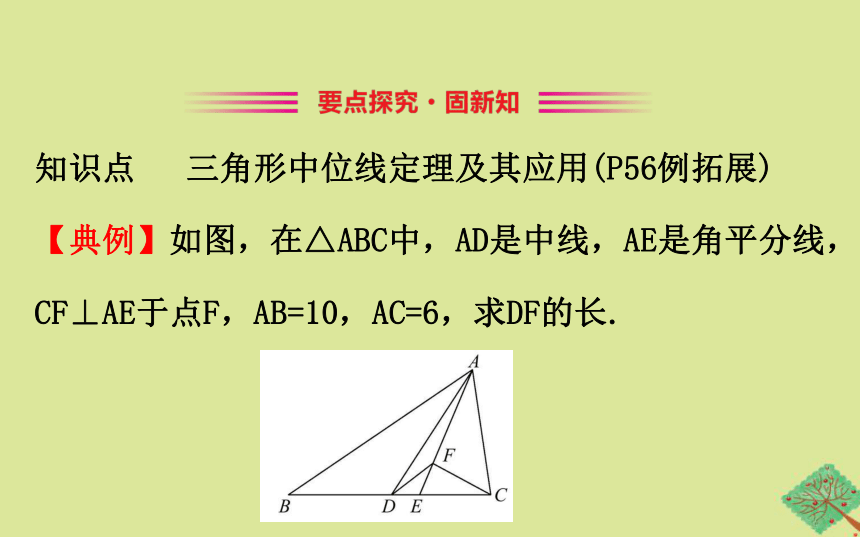
知识点 三角形中位线定理及其应用(P56例拓展)
【典例】如图,在△ABC中,AD是中线,AE是角平分线,CF⊥AE于点F,AB=10,AC=6,求DF的长.
【自主解答】
延长CF交AB于点G,
∵AE平分∠BAC,
∴∠GAF=∠CAF,
∴AF垂直平分CG,
∴AC=AG,GF=CF,
又∵点D是BC中点,∴DF是△CBG的中位线,
∴DF= BG= (AB-AG)= (AB-AC)= (10-6)=2.
【学霸提醒】
三角形中位线“定理”及“应用”
1.定理:有两个含义,一个表示位置关系,一个表示数量关系.
2.应用:在三角形中已知两边的中点时,可考虑构造三角形的中位线,根据三角形的中位线定理计算或证明.应用这个定理时,有时需要平行关系,有时需要倍分关系,用哪个结论应根据具体情况,灵活使用.
【题组训练】
1.如图,在平行四边形ABCD中,对角线AC,BD交于点
O,点E是BC的中点.若OE=3 cm,则AB的长为 ( )
A.3 cm B.6 cm
C.9 cm D.12 cm
B
★2.在△ABC中,D,E分别是边BC,AC的中点,BF平分
∠ABC,交DE于点F.AB=8,BC=6,则EF的长为 ( )
A.1
B.2
C.3
D.4
A
★3.(教材变形题·P56练习T1)已知三角形三边之比为
2∶3∶4,且此三角形的三条中位线围成的三角形的周
长是9,则原三角形的最长边是______.?
8
★★4.如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
证明:连接AC,在△ADC中,∵G,H分别是CD,DA的中
点,∴HG∥AC,HG= AC.在△ABC中,
∵E,F分别是AB,BC的中点,
∴EF∥AC,EF= AC,∴HG∥EF,HG=EF.
∴四边形EFGH是平行四边形.
【火眼金睛】
在Rt△ABC中,AC=5,BC=12,D为AC的中点,E为BC的中点,则DE的长为______.?
【正解】∵AC当AB为斜边时,AB= =13.
∵D为AC的中点,E为BC的中点.
∴DE= AB=6.5.
当BC为斜边时,AB=
∵D为AC的中点,E为BC的中点.
∴DE= AB= .
答案:6.5或
【一题多变】
△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.
证明:连接DE,FG,∵BD,CE是△ABC的中线,
∴D,E是AC,AB的中点,∴DE∥BC,DE= BC,
同理:FG∥BC,FG= BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,EF=DG.
【母题变式】
【变式一】(变换条件和问法)如图,在△ABC中,M是BC中点,AP是∠BAC的平分线,BP⊥AP于点P,AB=12,AC=22,求MP的长.
解:延长BP交AC于点N,
∵AP是∠BAC的平分线,BP⊥AP于点P,
∴∠BAP=∠NAP,∠APB
=∠APN=90°,
∴△ABP≌△ANP(ASA),∴AN=AB=12,BP=PN,
∴CN=AC-AN=22-12=10,
∵BP=PN,BM=CM,
∴PM是△BNC的中位线,∴PM= CN=5.
【变式二】(变换问法)如图,△ABC中,AD是高,E,F分别是AB,AC的中点.
(1)若AB=10,AC=8,求四边形AEDF的周长.
(2)EF与AD有怎样的位置关系?请证明你的结论.
略
2.4 三角形的中位线
【知识再现】
三角形的一个顶点与对边中点的连线叫三角形的中线.
【新知预习】阅读教材P55-P56,解决下面问题:
探究三角形的中位线及其性质
①任意画△ABC,设AB,AC,BC边的中点分别为D,E,F,连接DE,DF,EF.
定义:连接三角形两边的_________的线段,叫作三角
形的中位线,?
②三角形有______条中位线.?
③在图中分别度量∠ADE与∠B的大小,则∠ADE
______∠B,所以DE_______BC.分别量出线段DE与BC的
长,你发现DE=_________.?
中点
3
=
∥
? BC
④对于△ABC其他的两条中位线,重复③中的操作.
你发现的规律:
三角形的中位线_________于第三边,并且等于
_________________.?
平行
第三边的一半
【基础小练】
请自我检测一下预习的效果吧!
1.如图,在△ABC中,AB=8,∠C=90°,∠A=30°,
DE是中位线,则DE的长为 ( )
A
A.2 B.3
C.4 D.2
2.如图,在四边形ABCD中,点P是对角线BD的中点,点
E,F分别是AB,CD的中点,AD=BC,∠FPE=136°,则
∠PFE的度数是 ( )
A.15° B.20°
C.22° D.44°
C
知识点 三角形中位线定理及其应用(P56例拓展)
【典例】如图,在△ABC中,AD是中线,AE是角平分线,CF⊥AE于点F,AB=10,AC=6,求DF的长.
【自主解答】
延长CF交AB于点G,
∵AE平分∠BAC,
∴∠GAF=∠CAF,
∴AF垂直平分CG,
∴AC=AG,GF=CF,
又∵点D是BC中点,∴DF是△CBG的中位线,
∴DF= BG= (AB-AG)= (AB-AC)= (10-6)=2.
【学霸提醒】
三角形中位线“定理”及“应用”
1.定理:有两个含义,一个表示位置关系,一个表示数量关系.
2.应用:在三角形中已知两边的中点时,可考虑构造三角形的中位线,根据三角形的中位线定理计算或证明.应用这个定理时,有时需要平行关系,有时需要倍分关系,用哪个结论应根据具体情况,灵活使用.
【题组训练】
1.如图,在平行四边形ABCD中,对角线AC,BD交于点
O,点E是BC的中点.若OE=3 cm,则AB的长为 ( )
A.3 cm B.6 cm
C.9 cm D.12 cm
B
★2.在△ABC中,D,E分别是边BC,AC的中点,BF平分
∠ABC,交DE于点F.AB=8,BC=6,则EF的长为 ( )
A.1
B.2
C.3
D.4
A
★3.(教材变形题·P56练习T1)已知三角形三边之比为
2∶3∶4,且此三角形的三条中位线围成的三角形的周
长是9,则原三角形的最长边是______.?
8
★★4.如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
证明:连接AC,在△ADC中,∵G,H分别是CD,DA的中
点,∴HG∥AC,HG= AC.在△ABC中,
∵E,F分别是AB,BC的中点,
∴EF∥AC,EF= AC,∴HG∥EF,HG=EF.
∴四边形EFGH是平行四边形.
【火眼金睛】
在Rt△ABC中,AC=5,BC=12,D为AC的中点,E为BC的中点,则DE的长为______.?
【正解】∵AC
∵D为AC的中点,E为BC的中点.
∴DE= AB=6.5.
当BC为斜边时,AB=
∵D为AC的中点,E为BC的中点.
∴DE= AB= .
答案:6.5或
【一题多变】
△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.
证明:连接DE,FG,∵BD,CE是△ABC的中线,
∴D,E是AC,AB的中点,∴DE∥BC,DE= BC,
同理:FG∥BC,FG= BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,EF=DG.
【母题变式】
【变式一】(变换条件和问法)如图,在△ABC中,M是BC中点,AP是∠BAC的平分线,BP⊥AP于点P,AB=12,AC=22,求MP的长.
解:延长BP交AC于点N,
∵AP是∠BAC的平分线,BP⊥AP于点P,
∴∠BAP=∠NAP,∠APB
=∠APN=90°,
∴△ABP≌△ANP(ASA),∴AN=AB=12,BP=PN,
∴CN=AC-AN=22-12=10,
∵BP=PN,BM=CM,
∴PM是△BNC的中位线,∴PM= CN=5.
【变式二】(变换问法)如图,△ABC中,AD是高,E,F分别是AB,AC的中点.
(1)若AB=10,AC=8,求四边形AEDF的周长.
(2)EF与AD有怎样的位置关系?请证明你的结论.
略
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
